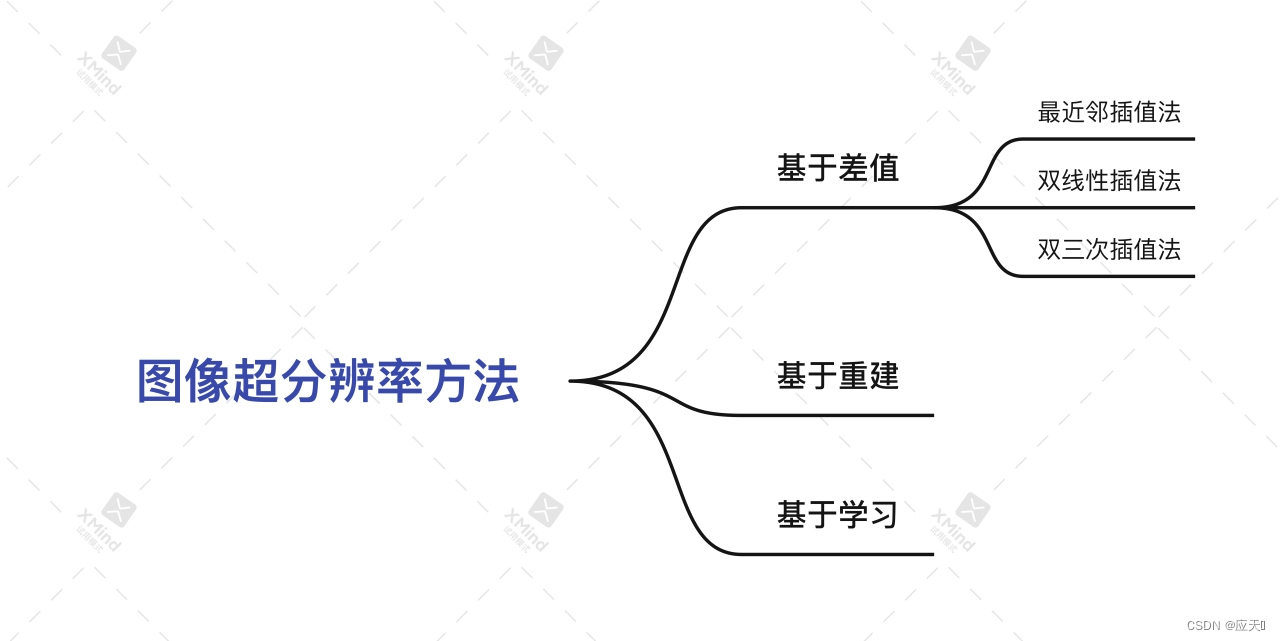
基于差值的图像超分辨率方法

图像超分辨率方法指的是使用一些方法将低分辨率的图像转换为高分辨率的图像。
在这里插入图片描述
传统的基于差值的图像超分辨率方法是指将利用像素间的相关性等特点，通过某些运算，对像素个数进行扩充（比如将64x64的图像扩充为512x512的图像）。

如上图所示，一张图像的取样点越多，我们看的越清楚。取样点越少，我们近视的度数越高。
在这里插入图片描述
但是如上图所示，原图像2x2的像素块，扩充为4x4的像素块以后，这16的像素值应该怎样取值呢。
目前主要有三种，即最近邻差值法、双线性差值法和双三次差值法。

最近邻插值法

最近邻插值法的思想很简单，就是近朱者赤近墨者黑。
在这里插入图片描述
以坐标轴为例，已知两点的x值和y值，如果给剩余的x值赋值，那么红色部分的x值取左边的y值，因为相比右边，它离得左边更近；同理，绿色部分的x值取右边的y值。
将上述思想应用到图像中，可以用下式表示。
$\begin{dcases} srcX=dstX \times \dfrac{srcWidth}{dstWidth} \\\\ srcY=dstY \times \dfrac{srcHeight}{dstHeight} \end{dcases}$
其中dstX和dstY是所需要扩充的像素点的坐标。srcWidth和srcHeight为原图像的宽和高（如原图像为2x2的像素块，则srcWidth=2，srcHeight=2）。dstWidth和dstHeight为扩展后图像的宽和高。扩展后的（dstX，dstY）为原图像的（srcX，srcY）位置的像素值。
在这里插入图片描述
如上图所示，想要填充的坐标位置为（3，2），原图像大小为2x2，想要变成4x4大小的图像。则，dstX=3，dstY=2，srcWidth=2，srcHeight=2，dstWidth=4，dstHeight=4。代入公式计算可得， srcX=1.5，srcX=1。经四舍五入，（3，2）点像素值为原图像（2，1）点的像素，也就是黄色。
在这里插入图片描述
上图为对每个位置进行计算后的结果。

单线性插值法

在这里插入图片描述
单线性插值法由我们初中时候学过的知识两点确定一条直线引入。
除了经典的y=kx+b以外，我们还学过一个两点式的方法来在坐标轴中描述一条直线。
$\dfrac{y-y1}{x-x1}=\dfrac{y2-y1}{x2-x1}$
经过简单的变化可以得到。
$y=\dfrac{x2-x}{x2-x1}y1+\dfrac{x-x1}{x2-x1}y2$
在这里插入图片描述
已知点（x1，y1）和点（x2，y2）代入上述式子求出直线的函数，如果我们想得到x点y的坐标，只需要将x点代入函数即可。
而对于图像来说，则需要四个点的参与。也就是说最近邻插值法生成的新位置的像素值只需要一个点的参与，而在单线性插值法中，需要原图像四个点的参与。
比如，经过最近邻插值法中提到的运算方法，新的像素值(x,y)落在原图像的四个像素值之间，如下图所示。
在这里插入图片描述
首先使用两点式生成f(x0,y1)和f(x0,y0)的直线函数，其中f(x0,y1)为图像在(x0,y1)位置的像素值，代入y，得到结果f(x0,y)。同理，得到f(x1,y)。

使用两点式生成f(x0,y)和f(x1,y0)的直线函数，代入x，即可得到所求的f(x,y)的值。
在这里插入图片描述
可以根据下图，方便理解。

双三次插值法

而双三次插值法则需要周围16个点的参与，这个方法也是这三个方法中恢复效果最好的。因此我们或许可以大胆推断，参与的点越多，越能实现更好的超分辨率效果。但是，相应的，计算量也会大很多。
在这里插入图片描述

双三次插值法的主要思想就是它的像素值是其周围16个像素值的赋予不同的权重之和。
对于点(i,j)，它为最终的像素值的贡献可以写为f(i,j)xw(u)xw(v)。其中，w()为权重函数，u和v为i+u和j+v到i和j的距离。
最终的结果可以用线性代数的方式表示如下。
$A\times B\times C$
$\begin{dcases} A= \begin{bmatrix*}[r] w(1+u)& w(u)& w(1-u)& w(2-u) \end{bmatrix*}\\ B= \begin{bmatrix*}[r] f(i−1,j−1)& f(i−1,j+0)& f(i−1,j+1)& f(i−1,j+2)\\f(i+0,j−1)&f(i+0,j+0)&f(i+0,j+1)&f(i+0,j+2)\\f(i+1,j−1)&f(i+1,j+0)&f(i+1,j+1)&f(i+1,j+2)\\f(i+2,j−1)&f(i+2,j+0)&f(i+2,j+1)&f(i+2,j+2) \end{bmatrix*}\\ C= \begin{bmatrix*}[r] w(1+v)&w(v)&w(1−v)&w(2−v) \end{bmatrix*}{^T}\eqslantless|{x}| \end{dcases}$
$w(x)=\begin{dcases} 1-2|{x}|^2+|{x}|^3 &\text{if } |{x}|<1 \\ 4-8|{x}|^2+5|{x}|^2-|{x}|^3&\text{if } 1\eqslantless|{x}|<2\\0&\text{if } 2\eqslantless|{x}| \end{dcases}$

方法对比

在这里，先将一张512x512的图像转换为64x64的，再用三种方法进行恢复。
在这里插入图片描述
可以看到，最近邻插值法有比较明显的马赛克效应，双三次插值法的恢复效果相对最好。