生成网络之Flow-based Generative Model

最近看关键点论文时发现，可以使用Flow-based生成网络去模拟生成真实潜在误差概率分布，从而增加Regression-based信息获取，大幅提高Regression-based方法的AP。为了真正搞懂这篇论文，我详细了解了Flow-based Generative Model的相关知识，并记录在这里，有不对的地方还请大佬指点。

Generator

首先，我们要知道Flow-based Generative Model实质上是一个生成器，生成器G定义了一个概率密度函数$P_G$,我们要做的就是让$P_G$无限接近$P_{data}$即真实样本分布。如何接近呢？这里需要了解极大似然估计的概念。

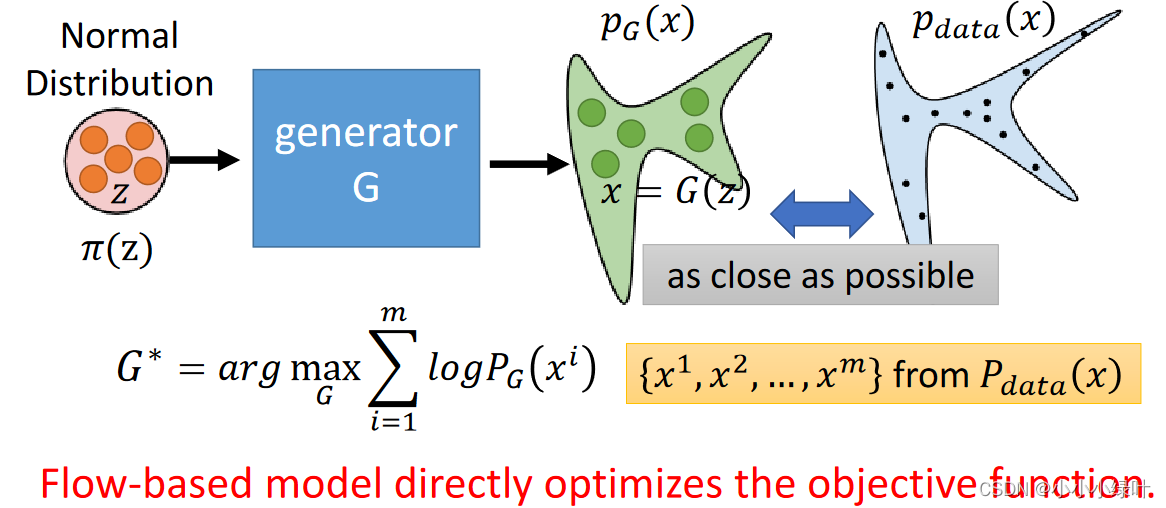
极大似然估计大概的意思是，我们已知一种概率密度函数，内部参数无法确定，但是我们可以进行大量试验，将试验结果代入函数中，求出概率最大的参数，即确定了概率密度函数。

这里的$P_G$就是一个随机参数的概率密度函数，我们从$P_{data}$真实样本分布中抽取样本$x^i$,将其带入$P_G(x^i)$,并max($log{P}_G(x^i)$),通过不断迭代就可以使$P_G$越来越接近$P_{data}$。原来大概是这样，下面介绍Flow-based Generative Model需要用的数学知识。

Math Background

1. 雅可比矩阵
首先，需要了解雅可比矩阵，已知$x=f(z),f$是关于z的函数，那$f$的雅可比矩阵就是上图的$J_f$。

2.行列式


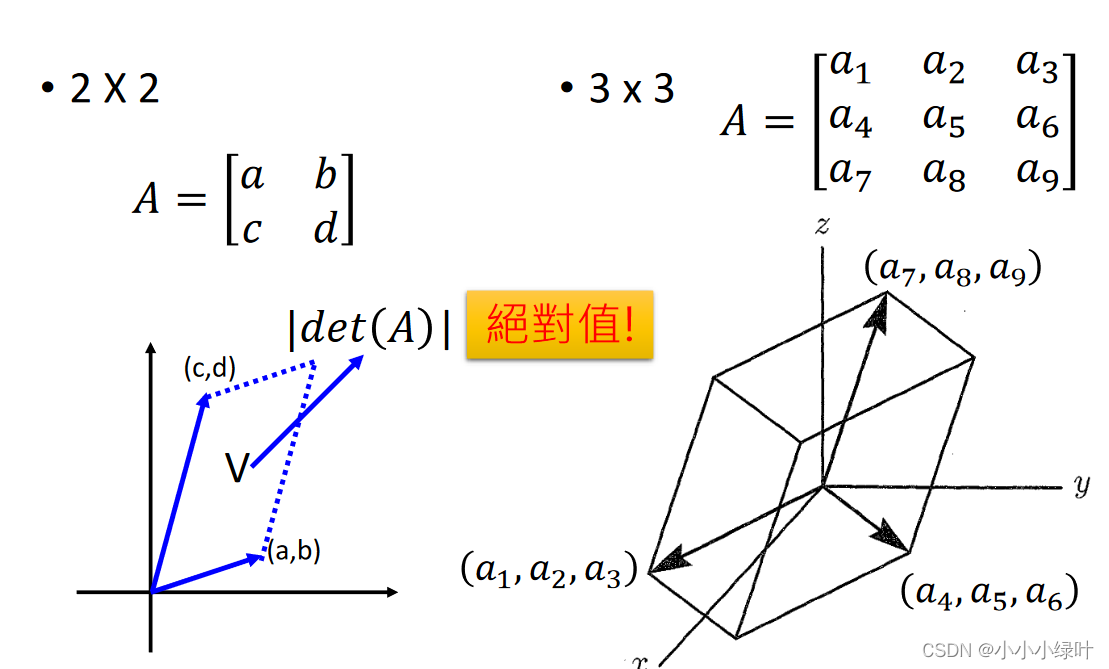
行列式的物理意义可以理解为以行作为向量的组成的多边形面积或体积。

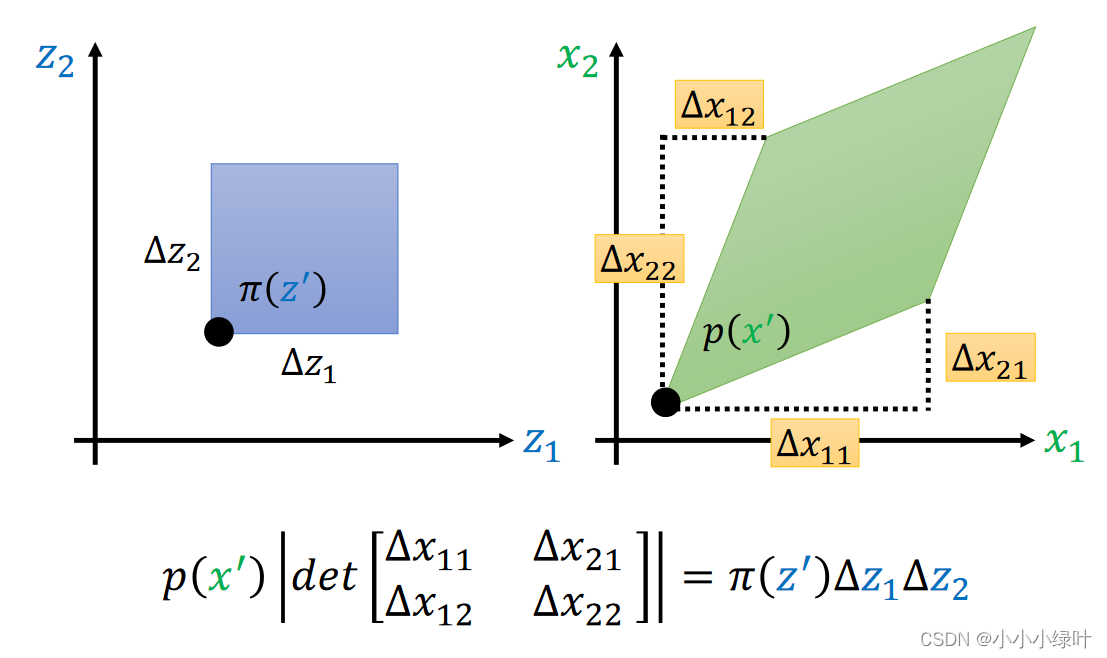我们已知两个概率密度函数$\pi (z),p(x)$,这两个概率密度函数存在$x=f(z)$这样的变化关系。根据两个函数对应部分积分的面积相等，即上图紫色的正方形与右边菱形面积相等（虽然看着不相等），可以得到上图的等式。等式可以这么理解，在$\Delta z,\Delta x$区间对$\pi (z),p(x)$进行积分，由于x通过$x=f(z)$可以映射到z，所以积分的面积（这里应该理解为体积）是可以保证不变的，变得只是$\Delta z,\Delta x$区间的面积以及$\pi (z),p(x)$的密度。又因为$\Delta z,\Delta x$区间足够小，在$\Delta z,\Delta x$区间上积分可以直接等效为$\Delta z,\Delta x$区间面积与密度相乘，而右边菱形的面积可以用行列式的绝对值表示，因此可以得到上图的等式。
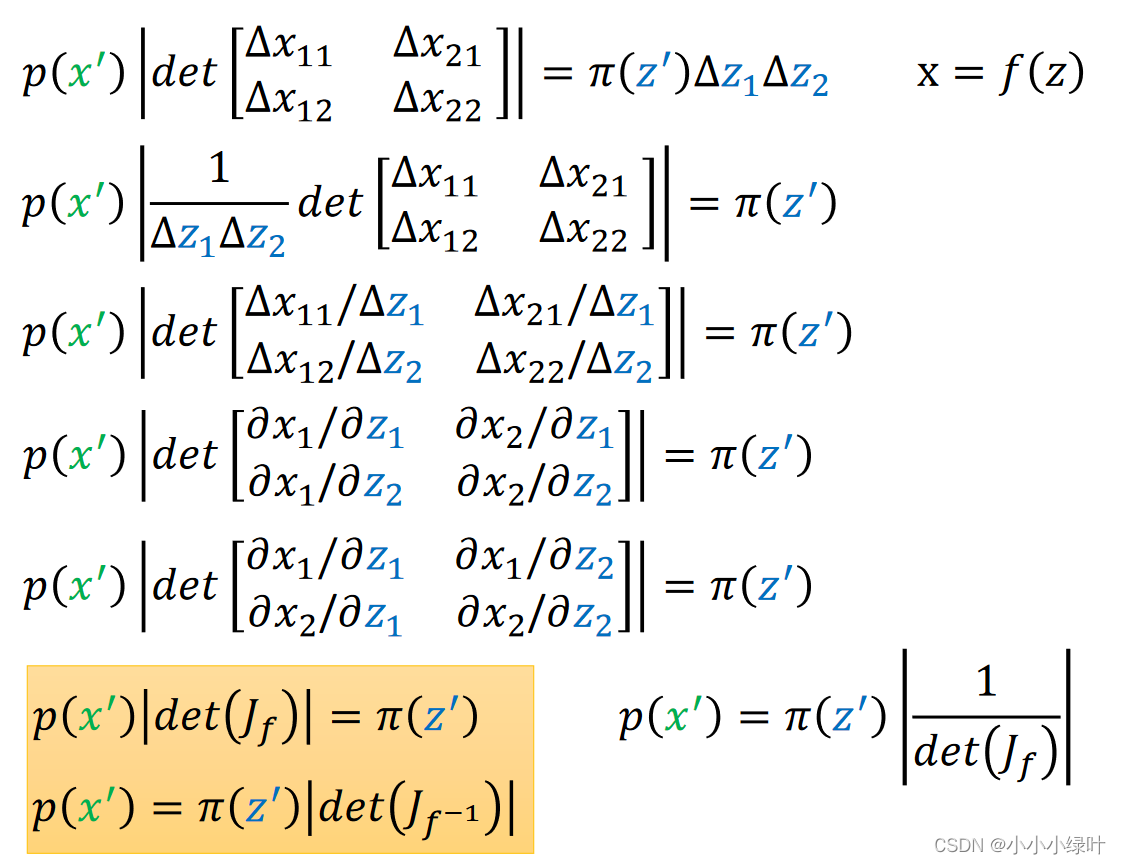通过上图一系列行列式等效变化，最终我们可以获得上图黄色框内的等式。即已知$x=f(z)$，$\pi (z),p(x)$可以根据$f$的雅可比矩阵的行列式绝对值相互映射。

Flow-based Generative

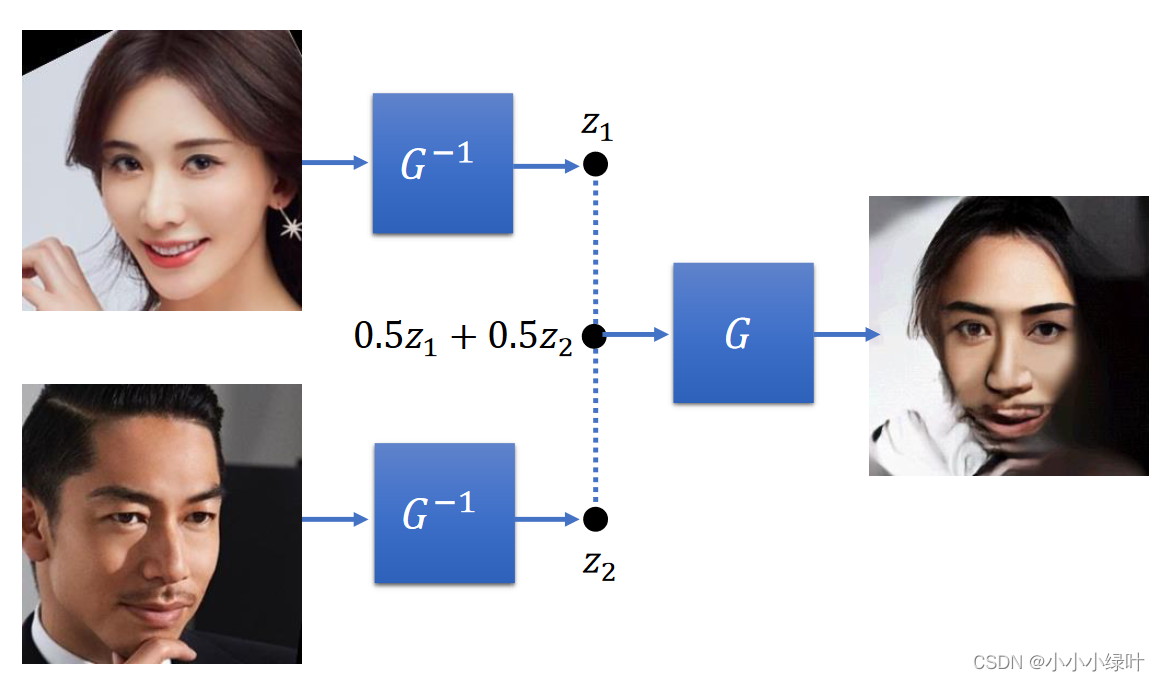
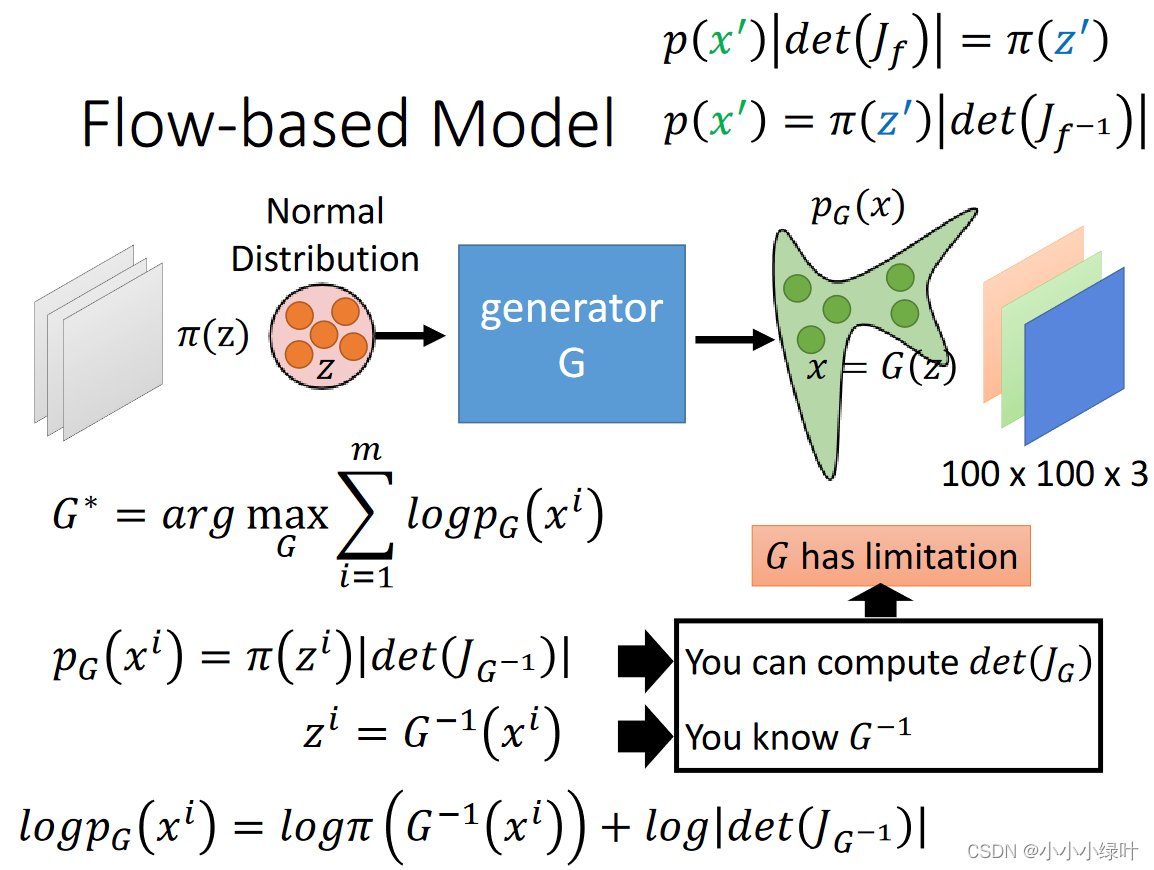在Flow-based model中，我们可以将神经网络作为G，$x^i$是来自真实分布的样本，当G可逆时，分别求出G的逆与雅可比矩阵就能够得到$p_G(x^i)$。因此，我们训练的是G的逆，而在推理时则是用的G。下图是Flow-based Generative应用的demo示例。