经典七大比较排序算法 · 下 + 附计数和基数排序
1 插入排序
1.1 算法思想
直接插入排序的基本思想就是,把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录都插入完为止,就得到一个新的有序序列。
只是看这种文字说明当然是有一点难以理解。其实在实际生活中,我们玩扑克牌时,就会不自觉地用到插入排序的思想。

我们可以从一端起,将新牌不断和手中的旧牌进行比较,来寻找合适的位置进行插入。插入之后保证手中的牌仍是有序的。
像扑克牌插入一样,这里给出直接插入排序的操作:
当插入第 i ( i ≥ 1 ) i(i\ge 1) i(i≥1)个元素时,前面的 a r r a y [ 0 ] , a r r a y [ 1 ] , … , a r r a y [ i − 1 ] array[0],array[1],…,array[i-1] array[0],array[1],…,array[i−1]已经排好序。此时用 a r r a y [ i ] array[i] array[i]的排序码和 a r r a y [ i − 1 ] , a r r a y [ i − 2 ] , . . . array[i-1],array[i-2],... array[i−1],array[i−2],...的排序码按顺序进行比较,找到待插入位置即可将 a r r a y [ i ] array[i] array[i]插入,原来位置上的元素要按顺序依次后移。
插入排序视频演示
1.2 代码实现
在了解了插入排序的大致思想之后,可以来尝试将其实现。
插入排序有一个前提是在有序序列中进行插入。
那如何一开始就整一个有序序列呢?嘿嘿,一开始让其只有一个元素,一个元素不就可以看做有序序列了吗。
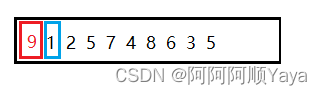
如图所示,要将上图数据进行排序。可以先将第一个数据9看做有序序列,让数据9后面的数据1对其进行插入排序。
这一次插入排序完成后,就得到如下图所示结果。
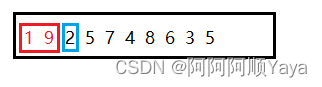
然后就是用数据2对前面的有序序列进行插入排序了。以此类推,如此反复。
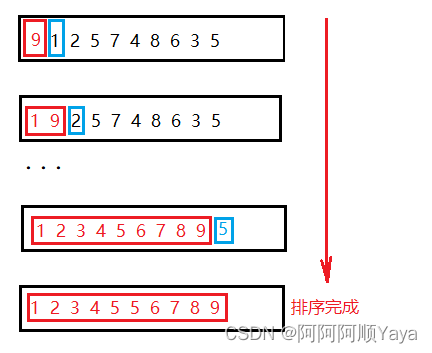
最终就可以将数据排好序了。
所以这里我们就可以假设一开始 [ 0 , e n d ] [0,end] [0,end]是排好序的(end从0开始),将 e n d + 1 end+1 end+1位置的数据对其前面的有序序列进行插入排序,直到最后一个数据插入排序完成,整个序列也就有序了。
但还有一个点需要注意。
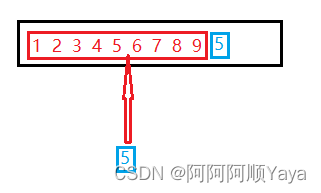
当插入数据时,可能是在序列之中进行插入。
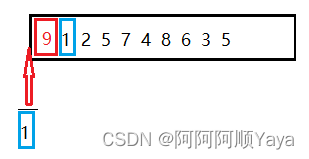
也可能是在序列最前面进行插入。
这两个地方的插入是略有不同的。因为这意味着插入排序两种不同的结束情况。需要有相应的判断条件来对插入排序进行终止。
鉴于以上的分析,这里给出如下参考实现代码:
//a - 待排序数组首地址
//n - 待排序数据个数
void InsertSort(int* a, int n)
{
int i = 0;
for (i = 0; i < n-1; ++i)
{
//[0,end]有序,把end+1位置的值插入,保持有序
//end区间为[0,n-2]
int end = i;
int tmp = a[end + 1];
//当end<0,代表在序列最前面进行插入的情况(如数据1的插入)
while (end >= 0)
{
if (tmp < a[end])
{
//依次向后挪动覆盖
a[end + 1] = a[end];
--end;
}
else
{
//tmp>=a[end],代表在序列中间进行插入的情况(如数据5的插入)
break;
}
}
//插入数据
a[end + 1] = tmp;
}
}
1.3 插入排序特性
直接插入排序的特性是,待排序的序列越接近有序的情况下,直接插入排序的时间效率会越高。
因为序列越接近有序的情况下,待排序的数据比较的次数会越少,数据挪动的次数回越少。此时的时间复杂度是接近 O ( n ) O(n) O(n)量级的。
但是,序列在无序情况下,或者最坏的逆序情况下,插入排序的时间复杂度是 O ( n 2 ) O(n^2) O(n2)量级的。

比如像上图这样,数据8插入排序挪动 1 下,数据7插入排序挪动 2 下,数据6插入排序挪动 3 下,. . . 。
最终操作步骤累加起来会是一个等差数列,也就是 O ( n 2 ) O(n^2) O(n2)量级的。
所以只能说,插入排序的适应性是很强的,在特定(接近有序)场景下的排序效果会非常出色。
2 希尔排序
希尔排序也称缩小增量排序,该方法因希尔(Donald Shell)于1959年提出而得名。

2.1 算法思想
希尔排序是对直接插入排序的优化改进,主要是基于插入排序的以下两点性质提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率是很高的,可以达到线性O(n)排序的效率。
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动1位。
针对以上两点,希尔大佬给出如下办法:
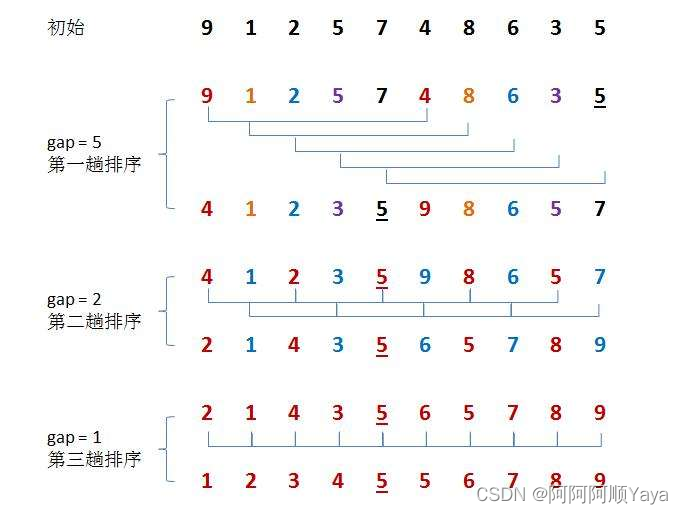
先选定一个整数gap,然后把待排序文件中的所有记录分成gap个组,所有距离为gap的记录分在同一组内,并对每一组内的记录进行直接插入排序。然后,不断缩小gap值,重复上述分组和排序的工作。当gap缩小到1时,所有记录在同一组内,进行直接插入排序,排完后记录就有序了。
总的来说,希尔排序分为两步:
- 第一步:
gap>1,分gap组,进行预排序 - 第二步:
gap=1,进行的是直接插入排序
这里第一步是针对插入排序第2点的劣势进行的改进。分成gap组,间隔为gap的数据为一组,每一次数据移动都是移动gap位,大大提高了排序的效率。
这里第二步是针对插入排序第1点的优势进行的利用。因为预排序的作用,使得记录已经处于接近有序的状态,这时利用插入排序很好的适应性,就可以实现非常高效的排序了。
但是,要说明的是,这个gap该如何选取呢?
1961年,IBM公司的女程序员 Marlene Metzner Norton(玛琳·梅茨纳·诺顿)首次使用 FORTRAN 语言编程实现了希尔排序算法。在其程序中使用了一种简易有效的方法设置希尔排序所需的增量序列(gap):第一个增量取待排序记录个数的一半,然后逐次减半,最后一个增量为1。该算法后来被称为 Shell-Metzner 算法,Metzner 本人在2003年的一封电子邮件中说道:“我没有为这种算法做任何事,我的名字不应该出现在算法的名字中。”
现在希尔排序的实现中对于gap的选取主要用的有两种,都是和记录个数n(gap=n)相关:
g a p = g a p / 3 + 1 gap=gap/3+1 gap=gap/3+1
g a p = g a p / 2 gap=gap/2 gap=gap/2
两种方法都能保证最后一次排序中,gap等于1。
2.2 代码实现
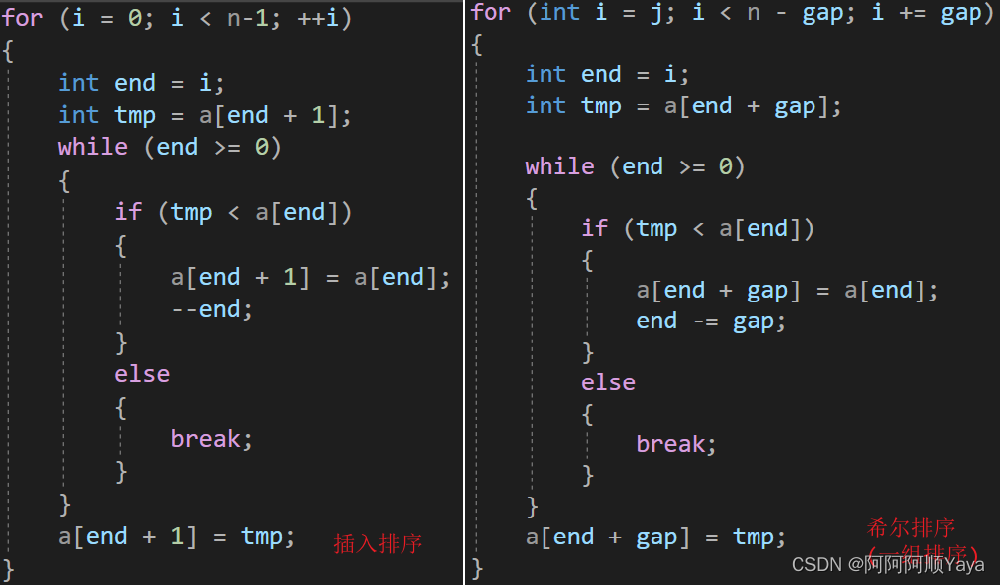
因为希尔排序的起源还是插入排序,只是分成了gap组的插入排序。所以在代码实现上是有部分相似性的,如下图所示。
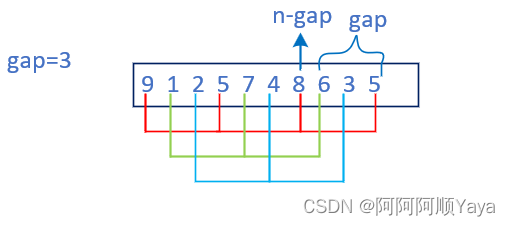
因为是分成gap组,所以一趟插入排序在希尔排序中只能排一组。所以执行gap次也就可以实现gap个组的插入排序了。
for (int j = 0; j < gap; ++j)
{
for (int i = j; i < n - gap; i += gap)
{
...
...
}
}
此时这样的一趟执行完之后,只是完成了一趟预排序。gap>1,仍需继续循环执行该操作。所以,
while (gap > 1)
{
gap = gap / 3 + 1;
for (int j = 0; j < gap; ++j)
{
for (int i = j; i < n - gap; i += gap)
{
...
...
}
}
}
通过上面的铺垫,下面就可以给出完整的希尔排序过程了。
//n - 数据个数
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int j = 0; j < gap; ++j)
{
for (int i = j; i < n - gap; i += gap)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
}
但是,上面的代码还可以进行一下优化。
for (int j = 0; j < gap; ++j)
{
for (int i = j; i < n - gap; i += gap)
{
...
...
}
}
//将两个循环合并成一个循环
for (int i = 0; i < n - gap; ++i)
{
...
...
}
这样就将原本是一组插入排序完之后再执行另一组的过程,转变成gap组交替执行的过程。
只是代码上的简化,大思想还是不变的。
2.3 希尔排序特性
希尔算法的性能与所选取的分组长度序列有很大关系。只对特定的待排序记录序列,可以准确地估算关键词的比较次数和对象移动次数。但想要弄清关键词比较次数和记录移动次数与增量选择之间的关系,并给出完整的数学分析,迄今仍然是数学上难题。
所以,希尔排序确切的时间复杂度是很难计算的,很多书上给出的希尔排序的时间复杂度也都不尽相同。
《数据结构(C语言版) – 严蔚敏》
希尔排序的分析是一个复杂度问题,因为它的时间是所取“增量”序列的函数,这涉及一些数学上尚未解决的难题。因此,到目前为止,尚未有人求得一种最好的增量序列,但大量的研究已得出一些局部的结论。如有人指出,当增量序列为 d l t a [ k ] = 2 t − k + 1 − 1 dlta[k]=2^{t-k+1}-1 dlta[k]=2t−k+1−1时,希尔排序的时间复杂度为 O ( n 3 / 2 ) O(n^{3/2}) O(n3/2),其中 t t t为待排序趟数, 1 ≤ k ≤ t ≤ l o g 2 ( n + 1 ) 1\leq k\leq t\leq log_2(n+1) 1≤k≤t≤log2(n+1)。还有人在大量的实验基础上推出:当 n n n在某个特定范围内,希尔排序所需的比较和移动次数约为 n 1.3 n^{1.3} n1.3,当 n → ∞ n\rightarrow\infin n→∞时,可减少到 n ( l o g 2 n ) 2 n(log_2n)^2 n(log2n)2。增量序列可以有各种取法,但需注意:应使增量序列中的值没有除 1 之外的公因子,并且最后一个增量值必须等于1。
《数据结构-用面向对象方法与C++描述》-- 殷人昆
gap的取法有多种。最初Shell提出取 g a p = [ n / 2 ] gap=[n/2] gap=[n/2], g a p = [ g a p / 2 ] gap=[gap/2] gap=[gap/2],直到 g a p = 1 gap=1 gap=1,后来Knuth提出取 g a p = [ g a p / 3 ] + 1 gap=[gap/3]+1 gap=[gap/3]+1。还有人提出取奇数为好,也有人提出各 g a p gap gap互质为好。无论哪一种主张都没有得到证明。
对希尔排序的时间复杂度的分析很困难,在特定情况下可以准确地估算关键码的比较次数和对象移动次数,但想要弄清关键码比较次数和对象移动次数与增量选择之间的依赖关系,并给出完整的数学分析,还没有人能够做到。在Knuth所著的《计算机程序设计技巧》第3卷中,利用大量的实验统计资料得出,当 n n n很大时,关键码平均比较次数和对象移动次数大约在 n 1.25 n^{1.25} n1.25到 1.6 n 1.25 1.6n^{1.25} 1.6n1.25范围内,这是利用直接插入排序作为子序列排序方法的情况下得到的。
上面代码中的gap是按照Knuth提出的方式取值的。而Kunth进行了大量的试验统计,所以上面代码实现的希尔排序时间复杂度可以用 O ( n 1.25 ) O(n^{1.25}) O(n1.25)到 O ( 1.6 ∗ n 1.25 ) O(1.6*n^{1.25}) O(1.6∗n1.25)这个范围作参考。
3 七大比较排序特性总结
稳定性介绍:
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次
序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则这种排序算法是稳定的;否则是不稳定的。
| 排序算法 | 最好时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|
| 直接插入排序 | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 希尔排序 | 取平均时间复杂度: O ( n 1.3 ) O(n^{1.3}) O(n1.3) | \ | O ( 1 ) O(1) O(1) | 不稳定 |
| 选择排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 堆排序 | O ( n ∗ l o g 2 n ) O(n*log_2n) O(n∗log2n) | O ( n ∗ l o g 2 n ) O(n*log_2n) O(n∗log2n) | O ( 1 ) O(1) O(1) | 不稳定 |
| 冒泡排序 | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 快速排序 | O ( n ∗ l o g 2 n ) O(n*log_2n) O(n∗log2n) | O ( n 2 ) O(n^2) O(n2) | O ( l o g 2 n ) O(log_2n) O(log2n) | 不稳定 |
| 归并排序 | o ( n ∗ l o g 2 n ) o(n*log_2n) o(n∗log2n) | o ( n ∗ l o g 2 n ) o(n*log_2n) o(n∗log2n) | O ( n ) O(n) O(n) | 稳定 |
4 计数排序
4.1 算法思想
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中,是对哈希直接定址法的变形应用。
操作步骤:
- 找出待排序的数组中最大和最小的元素
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
计数排序视频演示
4.2 代码实现
void CountSort(int* a, int n)
{
//找出待排序的数组中最大和最小的元素
int min = a[0];
int max = a[0];
for (int i = 1; i < n; ++i)
{
if (a[i] < min)
{
min = a[i];
}
if (a[i] > max)
{
max = a[i];
}
}
//统计次数的数组
int range = max - min + 1;
int* countArray = (int*)calloc(range, sizeof(int));
assert(countArray);
//统计次数
for (int i = 0; i < n; ++i)
{
++countArray[a[i] - min];
}
//回写-排序
int j = 0;
for (int i = 0; i < range; ++i)
{
//出现几次就回写几个min+i
while (countArray[i]--)
{
a[j++] = min + i;
}
}
}
上面代码采用了相对映射而非绝对映射,如果使用绝对映射,空间可能浪费太严重。
4.3 计数排序特性
计数排序以及桶排序,计数排序作为非比较排序,一般都只能用于对整数的排序,可用范围比较窄。
计数排序的局限性:
- 如果是浮点数,字符串等就不能用了
- 如果数据范围很大,空间复杂度会很高,相对不适合。(适合范围集中,重复数据多)
但在适用的场景下,时间复杂的是很好的,一般都是线性时间复杂度。
5 基数排序
5.1 算法思想
基数排序是一种借助多关键字排序的思想对单逻辑关键字进行排序的方法。
其核心思想是对数据的分发和回收。
基数排序视频演示
5.2 代码实现
计数排序的实现需要借助队列来完成,因为是使用C语言实现,如果需要可以参考阿顺的这篇博文链式队列(C语言实现)。
这里按照LSD法,即最低为优先来进行计数排序。
//首先建立RADIX(基数)个队列
Queue queue[RADIX];
for (int i = 0; i < RADIX; ++i)
{
QueueInit(&queue[i]);
}
//[left, right)
void RadixSort(int* a, int left, int right)
{
//K - 数据最高的位数
for (int i = 0; i < K; ++i)
{
//分发数据
Distribute(a, left, right, i);
//回收数据
Collect(a);
}
}
int getKey(int value, int k)
{
int key = 0;
while (k >= 0)
{
key = value % 10;
value /= 10;
--k;
}
return key;
}
void Distribute(int* a, int left, int right, int k)
{
for (int i = left; i < right; ++i)
{
//获取这一趟分发,a[i]数据的基数值
int key = getKey(a[i], k);
QueuePush(&queue[key], a[i]);
}
}
void Collect(int* a)
{
int j = 0;
for (int i = 0; i < RADIX; ++i)
{
while (!QueueEmpty(&queue[i]))
{
a[j++] = QueueFront(&queue[i]);
QueuePop(&queue[i]);
}
}
}
最后不要忘了销毁队列。