前言

记录在学数字信号处理过程中一些个人理解与感悟，本文主要讲的是采样定理在Matlab实现，在此之前会先讲一下傅里叶变换以及采样定理的公式推导等等，本人才疏学浅，此文可能难免出现错误之处，读者如有发现，望请斧正！

采样

为什么需要采样

首先，我们知道很多信号都是连续的，时间间隔是无穷小的，即在一个区间里面有无限个值，当我们使用计算机去处理信号，由于计算机的内存有效，只能完成有限的数据存储和运算，所以将模拟信号用计算机去处理的时候，我们就必须先对模拟信号进行抽样，使其变成离散时间信号，这样就可以使用计算机去处理了，当信号处理完后再将其抽样信号通过一些规则恢复成连续状态即可。

数字信号处理是对模拟信号进行处理的一种方式，最终可归结为对模拟信号进行处理数字信号处理不能对模拟信号产生根本性的改变。

采样是什么

首先需要先说明这里只研究等间隔采样的理想采样，其他采样方式和实际采样不在讨论范围之内。采样是利用周期性抽样脉冲信号从连续信号中，等间隔离散点上抽取模拟信号值，得到抽样信号。

扫描二维码关注公众号，回复： 14709841 查看本文章

采样过程如下图所示

其中T是采样间隔， $f_{s} = 1/T$ 是采样频率， $\Omega_{s} = 2\pi f_{s}$ 是采样角频率， $\hat{x} _{a}(t)$ 是理想抽样信号上述采样过程从时域上看

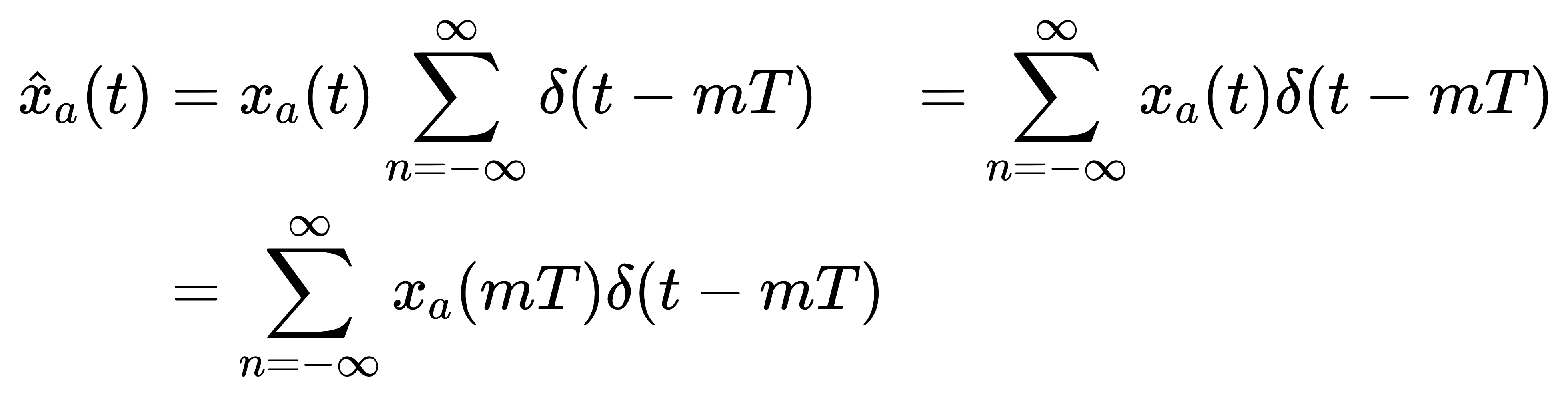
从频域上看

下面需要用到傅里叶变换，先放公式回忆一下

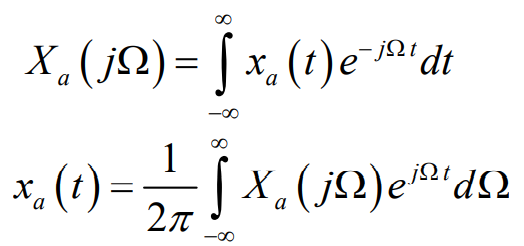
需要注意的是脉冲冲击串的傅里叶变换仍然为脉冲串，这个通过上面的傅里叶公式可以推出

信号与冲击串频域卷积后的信号是原信号向脉冲所在的位置的平移，即频谱搬迁，记住这句话比记住下面公式重要。

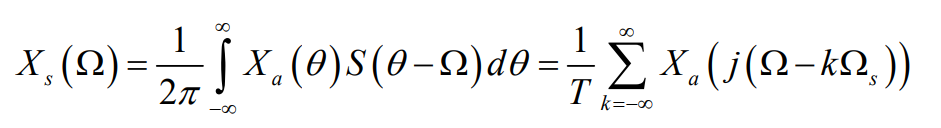
频谱搬迁这个结论说明了输出信号是原信号频谱以采样频率为重复周期的频域延拓，那就会存在一个问题，不同的采样频率采的出来的频谱不一样，有些稀疏，有些密集，当密集到一定程度就会出现混叠，那样我们就不能通过一个滤波器把原信号的频谱给滤出来，进而采样过程变成了不可逆过程，频域图可以看出了原信号的最高频率是 $\Omega_{N}$ ，相邻两个频谱相切时中心频率相差 $\Omega_{S}$ ，要不混叠即要满足 $\Omega_{S} \geq 2\Omega_{N}$ 。

这里想插一张网上看到的时域和频域的关系图，我觉得很形象的展示了两者的关系

奈奎斯特采样定理

前面我们提到了想要不混叠就必须满足 $\Omega_{S} \geq 2\Omega_{N}$ ，其实这里所提到的 $\Omega_{N}$ 就是我们的奈奎斯特频率。

令 $x_{a}(t)$ 是一个带限信号，则

$X_{a}(j\Omega) = 0 \ \ \ \ \ \ \ for \left |\Omega \right | \geq \Omega_{N}$

那么 $x_{a}(t)$ 可以由其采样 $x[n] = x_{a}(nT)$ 唯一确定

$\Omega_{S} = \frac{2\pi}{T} = 2\pi f_{s} \geq 2\Omega_{N}$

即想要采样后能够不失真地还原出原信号，则采样信号必须大于信号最高频率的两倍。

上述讲的是理想情况，而非实际情况，实际情况得需要使用A/D转换器，所获得的数字信号是在幅度和时间上量化的信号

采样恢复

在前面呢，我们讨论了与采样相关的知识，并且知道采样想要被完全恢复，就必须要满足奈奎斯特定理，采样完成后，我们就应该说一说采样恢复，也就是将离散时间信号变回连续时间信号。

由采样可知，采样后的频谱是原频谱的复制粘贴，我们只需要通过一个理想低通滤波器，那么就可以得到原信号的频谱。

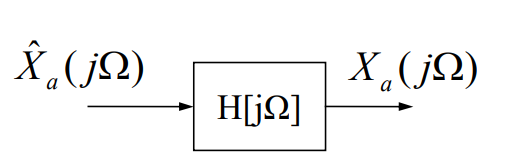
按照这个想法，我们说需要的低通滤波器以下长这样子

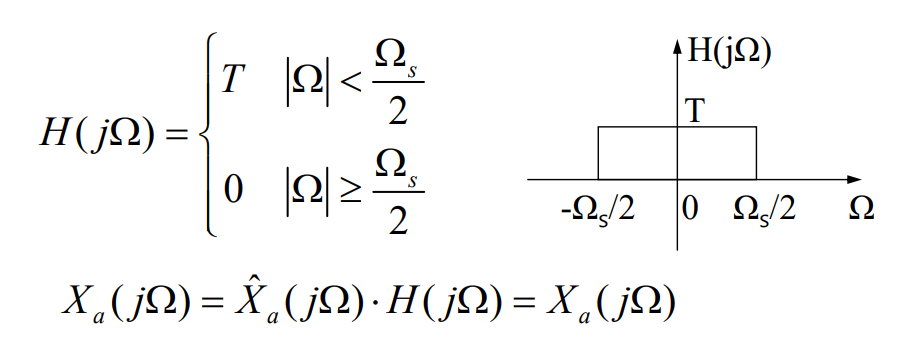
其中T是采样间隔， $f_{s} = 1/T$ 是采样频率， $\Omega_{s} = 2\pi f_{s}$ 是采样角频率， $\hat{X} _{a}(j\Omega )$ 是采样后的频域。

下面将结合公式推导一下如何进行采样恢复。

根据上面频域相乘可知恢复信号等于抽样信号与低通滤波器的冲激响应做卷积， $\hat{x}_{a}(t)$ 我们前面已知

$\hat{x}_{a}(t) = \sum_{n = -\infty}^{\infty}x_{a}(t)\delta(t-nT)$

现在我们得把 $h(t)$ 求出来，根据傅里叶公式有

$h(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty}H(j\Omega)e^{j\Omega t}d\Omega = \frac{T}{2\pi}\int_{-\Omega_{s}/2}^{-\Omega_{s}/2}e^{j\Omega t}d\Omega = \frac{sin(\frac{\Omega_{s}}{2}t)}{\frac{\Omega_{s}}{2}t} = \frac{sin(\frac{\pi}{T}t)}{\frac{\pi}{T}t}$

即理想低通滤波器的冲激响应是Sa(t)类型，它称之为抽样函数。

接下来就是做卷积运算,具体过程如下

到这里，我们已经推导出看信号重构的公式，其中 $h(t-mT)=\frac{sin[\frac{\pi}{T} (t-mT)]}{\frac{\pi}{T} (t-mT)}$ 称为内插函数，其图像如左下图。采样后的信号 $x_{a}(mT)$ 经过内插函数，得到连续信号 $x_{a}(t)$ ，如右下图

下面讲一下信号重构公式的意义，由公式我们可以知道，内插公式在抽样点mT上，函数值为1，其他抽样点上，函数值为零，不影响其他抽样点，也就是说， $x_{a}(t)$ 等于各 $x_{a}(mT)$ 乘于对应的内插函数的总和，在每一个抽样点上，只有对应的内插函数为零，这使得各抽样点上信号值不变，而抽样点之间的信号则由各加权抽样函数波形的延伸叠加而成，因此h(t)的作用就是在各抽样点之间连续插值的作用。

所以信号重构公式也说明了，只要抽样频率大于两倍信号最高频率，则原信号的整个频谱就会完整保留下来，从而整个连续信号时间信号就可以完全由它的抽样值代表，而不会丢失任何信息，这也是奈奎斯特采样定理的意义。

不过理想低通滤波器的频域特性是突变的，实际上不可实现，但是我们可以采用频域缓变的可实现滤波器来逼近理想低通滤波器，所以实际上也是不能完全不失真得重构出原信号，但是在误差范围允许内即可。

采样定理Matlab仿真（含代码）

验证采样定理，首先先需要画出原信号，在这里我写的原信号为两个正弦信号叠加，接着使用15Hz，20Hz，50Hz分别采样与恢复，对于每个信号我都画了时域和频域的图。

其中频域表示和信号重构方式都是用了矩阵相乘的方法实现运算，也可以使用for循环一个一个算。

%. 采样定理验证
%参数设定
t=-0.2:0.0005:0.2;%信号长度
%两个正弦函数的频率
f1 = 5;
f2 = 10;
k = -1 : 0.0001 : 1;
W = k / 0.0005 ; %频域范围

%原信号
f_origin = 0.5* sin(2 * pi * f1 * t)-cos(2 * pi * f2 * t);
F_origin = f_origin * exp(-1i * t' * W) * 0.0005;% 乘0.0005是dt
F_origin = abs(F_origin);% 复数没法画图，取绝对值
figure(6);
subplot(4,2,1);plot(t , f_origin);title('原信号');grid on;
subplot(4,2,2);plot(W , F_origin);title('原信号频谱');grid on;
% 频域表示


%20hz采样
fs = 20;
Ts = 1 / fs;
n = -0.2 : 1/fs : 0.2;%采样点
f_20Hz = 0.5 * sin(2 * pi * f1 * n) - cos(2 * pi * f2 * n);
F_20Hz = f_20Hz * exp(-1i * n' * W) * Ts;
F_20Hz = abs(F_20Hz);
figure(6);
subplot(4,3,7);stem(n,f_20Hz);title('20hz采样信号');grid on;
subplot(4,3,8);plot(W,F_20Hz);title('20hz采样信号频谱');grid on;
%20Hz恢复
t = -0.2 : 0.0005 : 0.2;
y = f_20Hz * sinc((ones(length(n),1)*t - n'*ones(1,length(t))) * fs);
subplot(4,3,9);plot(t,y);title('20Hz恢复');grid on;
%20Hz误差
figure(7);
error = abs(y - f_origin);
subplot(3,1,2);plot(t,error);title('20Hz误差');grid on;

%50hz采样
fs = 50;
Ts = 1 / fs;
n = -0.2 : 1/fs : 0.2;%采样点
f_50Hz = 0.5 * sin(2 * pi * f1 * n) - cos(2 * pi * f2 * n);
F_50Hz = f_50Hz * exp(-1i * n' * W) * Ts;
F_50Hz = abs(F_50Hz);
figure(6);
subplot(4,3,10);stem(n,f_50Hz);title('50hz采样信号');grid on;
subplot(4,3,11);plot(W,F_50Hz);title('50hz采样信号频谱');grid on;
%50Hz恢复
t = -0.2 : 0.0005 : 0.2;
y = f_50Hz * sinc((ones(length(n),1)*t - n'*ones(1,length(t))) * fs);
subplot(4,3,12);plot(t,y);title('50Hz恢复');grid on;
%50Hz误差
figure(7);
error = abs(y - f_origin);
subplot(3,1,3);plot(t,error);title('50Hz误差');grid on;

得到的图如下

可以看出在不满采样定理的时候，信号不能被完全重构，而在满足采样定理后，信号在误差允许的范围内恢复的与原信号基本一致，下图为误差图，可以看出采样频率越高，误差越小，而且误差呈现两边大中间小的趋势（这个我也不知道为什么）

连续时间信号的采样与恢复 Matlab仿真

目录

前言

采样

为什么需要采样

采样是什么

奈奎斯特采样定理

采样恢复

采样定理Matlab仿真（含代码）

猜你喜欢