支持向量机求解过程的可视化及其核函数kernel 【Tsai Tsai】

1.支持向量机分类器是如何工作的？

2. sklearn.svm.SVC

2.1 线性SVM决策过程的可视化

2.2 参数说明

2.3 非线性数据集上的推广与3D可视化

3. SVC的重要参数kernel

3.1 在sklearn中实现SVC的基本流程：

3.2 kernel

3.3 月亮型、环型、簇型、分类型在4个核函数不同的表现

1.支持向量机分类器是如何工作的？

支持向量机所作的事情其实非常容易理解。先来看看下面这一组数据的分布，这是一组两种标签的数据，两种标签分别由圆和方块代表。支持向量机的分类方法，是在这组分布中找出一个超平面作为决策边界，使模型在数据上的分类误差尽量接近于小，尤其是在未知数据集上的分类误差（泛化误差）尽量小。

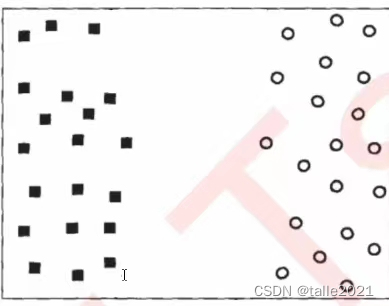
超平面

在几何中，超平面是一个空间的子空间，它是维度比所在空间小一维的空间。如果数据空间本身是三维的，则其超平面是二维平面，而如果数据空间本身是二维的，则其超平面是一维的直线。

在二分类问题中，如果一个超平面能够将数据划分为两个集合，其中每个集合中包含单独的一个类别，我们就说这个超平面是数据的“决策边界”。

决策边界一侧的所有点在分类为属于一个类，而另一侧的所有点分类属于另一个类。如果我们能够找出决策边界，分类问题就可以变成探讨每个样本对于决策边界而言的相对位置。比如上面的数据分布，我们很容易就可以在方块和圆的中间画出一条线，并让所有落在直线左边的样本被分类为方块，在直线右边的样本被分类为圆。如果把数据当作我们的训练集，只要直线的一边只有一种类型的数据，就没有分类错误，我们的训练误差就会为0。但是，对于一个数据集来说，让训练误差为0的决策边界可以有无数条。

但在此基础上，我们无法保证这条决策边界在未知数据集（测试集）上的表现也会优秀。对于现有的数据集来说,我们有 $B_{1}$ 和 $B_{2}$ 两条可能的决策边界。我们可以把决策边界 $B_{1}$ 向两边平移，直到碰到离这条决策边界最近的方块和圆圈后停下，形成两个新的超平面，分别是 $b_{11}$ 和 $b_{12}$ ，并且我们将原始的决策边界移动到 $b_{11}$ 和 $b_{12}$ 的中间，确保 $B_{1}$ 到 $b_{11}$ 和 $b_{12}$ 的距离相等。在 $b_{11}$ 和 $b_{12}$ 中间的距离，叫做 这条决策边界的边际 (margin)，通常记作 $d$ 。对 $B_{2}$ 也执行同样的操作，然后我们来对比一下两个决策边界。现在两条决策边界右边的数据都被判断为圆，左边的数据都被判断为方块，两条决策边界在现在的数据集上的训练误差都是0 ，没有一个样本被分错。

我们引入和原本的数据集相同分布的测试样本（红色所示），平面中的样本变多了，此时我们可以发现，对于 $B_{1}$ 而言，依然没有一个样本被分错，这条决策边界上的泛化误差也是0。但是对于 $B_{2}$ 而言，却有三个方块被误分类成了圆，而有两个圆被误分类成了方块，这条决策边界上的泛化误差就远远大于 $B_{1}$ 了。这个例子表现出，拥有更大边际的决策边界在分类中的泛化误差更小，这一点可以由结构风险最小化定律来证明（SRM）。如果边际很小，则任何轻微扰动都会对决策边界的分类产生很大的影响。边际很小的情况，是一种模型在训练集上表现很好，却在测试集上表现糟糕的情况，所以会“过拟合”。所以我们在找寻决策边界的时候，希望边际越大越好。

支持向量机，就是通过找出边际最大的决策边界，来对数据进行分类的分类器。 也因此，支持向量分类器又叫做最大边际分类器。

2. sklearn.svm.SVC

class sklearn.svm.SVC ( C=1.0 , kernel=’rbf’ , degree=3 , gamma=’auto_deprecated’ , coef0=0.0 , shrinking=True , probability=False , tol=0.001 , cache_size=200 , class_weight=None , verbose=False , max_iter=-1 , decision_function_shape=’ovr’ , random_state=None )

2.1 线性SVM决策过程的可视化

from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
x,y=make_blobs(n_samples=50,centers=2,random_state=0,cluster_std=0.6) #簇的方差=0.6
x.shape

(50, 2)

plt.scatter(x[:,0],x[:,1],c=y,s=50,cmap="rainbow")
plt.xticks([])
plt.yticks([])
plt.show()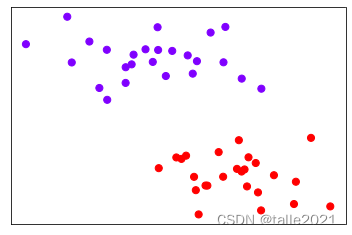

#画决策边界：制作网格
plt.scatter(x[:,0],x[:,1],c=y,s=50,cmap="rainbow")
#获取当前的子图，如果不存在，则创建新的子图
ax=plt.gca()
#获取平面上两条坐标轴的最大值和最小值
xlim=ax.get_xlim()
ylim=ax.get_ylim()
#在最大值和最小值之间形成30个规律的数据
axisx=np.linspace(xlim[0],xlim[1],30) 
axisy=np.linspace(ylim[0],ylim[1],30)
#使用meshgrid函数将两个一维向量转换为特征矩阵
axisy,axisx=np.meshgrid(axisy,axisx)
xy=np.vstack([axisx.ravel(),axisy.ravel()]).T
#其中ravel()是降维函数，vstack能够将多个结构一致的一维数组按行堆叠起来
# xy就是已经形成的网格，它是遍布在整个画布上密集的点
plt.scatter(xy[:,0],xy[:,1],s=1,cmap="rainbow")

<matplotlib.collections.PathCollection at 0x26d6f2838b0>

重要接口decision_function,返回每个输入的样本所对应的到决策边界的距离，然后再将这个距离转换为axisx的结构，这是由于画图的函数contour要求z的结构必须与x和y保持一致

# 建模。通过fit计算出对应的决策边界
clf=SVC(kernel="linear").fit(x,y)
z=clf.decision_function(xy).reshape(axisx.shape)
plt.scatter(x[:,0],x[:,1],c=y,s=50,cmap="rainbow")
ax=plt.gca()
# 画出决策边界和平行于决策边界的超平面
ax.contour(axisx,axisy,z #横坐标，纵坐标，高度
          ,colors="k"
          ,levels=[-1,0,1] #画三条等高线，分别是z为-1,0,1的三条线
          ,alpha=0.5
          ,linestyles=["--","-","--"])
ax.set_xlim(xlim)
ax.set_ylim(ylim)

为了便于更好地理解SVM作用原理，我们去第10个点作为例子：(z的本质是输入的样本到决策边界的距离，而contour函数中的level其实是输入了这个距离)

plt.scatter(x[:,0],x[:,1],c=y,s=50,cmap="rainbow")
plt.scatter(x[10,0],x[10,1],c="black",s=50,cmap="rainbow")
clf.decision_function(x[10].reshape(1,2))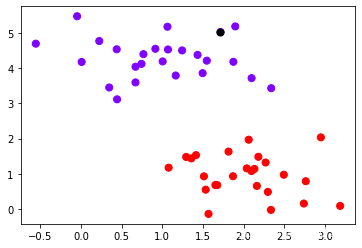

array([-3.33917354])

plt.scatter(x[:,0],x[:,1],c=y,s=50,cmap="rainbow")
ax=plt.gca()
ax.contour(axisx,axisy,z
          ,colors="k"
          ,levels=[-3.33917354]
          ,alpha=0.5
          ,linestyles=["--"])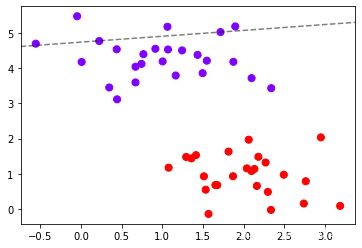

对上述过程包装成函数：

def plot_svc_decision_function(model,ax=None):
    if ax is None:
        ax=plt.gca()
    xlim=ax.get_xlim()
    ylim=ax.get_ylim()
    
    x=np.linspace(xlim[0],xlim[1],30)
    y=np.linspace(ylim[0],ylim[1],30)
    Y,X=np.meshgrid(y,x)
    xy=np.vstack([X.ravel(),Y.ravel()]).T
    p=model.decision_function(xy).reshape(X.shape)
    
    ax.contour(X,Y,p
              ,colors="k"
              ,levels=[-1,0,1]
              ,alpha=0.5
              ,linestyles=["--","-","--"])
    ax.set_xlim(xlim)
    ax.set_ylim(ylim)


clf=SVC(kernel="linear").fit(x,y)
plt.scatter(x[:,0],x[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)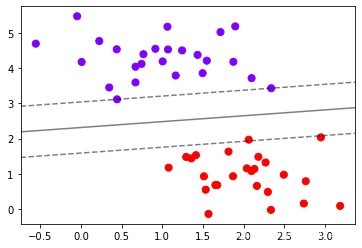

2.2 参数说明

根据决策边界，对x中样本进行分类，返回的结构为n_samples

clf.predict(x)

array([1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1,
       1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1,
       0, 1, 1, 0, 1, 0])

返回给定测试数据和标签的平均准确度

clf.score(x,y)

1.0

返回支持向量

clf.support_vectors_

array([[0.44359863, 3.11530945],
       [2.33812285, 3.43116792],
       [2.06156753, 1.96918596]])

返回每个类中支持向量的个数

clf.n_support_

array([2, 1])

2.3 非线性数据集上的推广与3D可视化

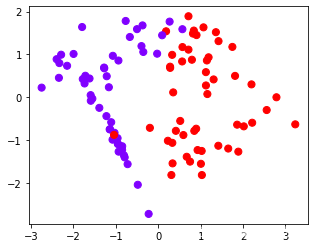
from sklearn.datasets import make_circles
x,y=make_circles(100,factor=0.1,noise=0.1)
plt.scatter(x[:,0],x[:,1],c=y,s=50,cmap="rainbow")
plt.show()

clf=SVC(kernel="linear").fit(x,y)
plt.scatter(x[:,0],x[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)
clf.score(x,y)

0.69

定义一个由x计算出来的新维度r

r=np.exp(-(x**2).sum(1))
rlim=np.linspace(min(r),max(r),100)
from mpl_toolkits import mplot3d
# 定义一个绘制三维图像的函数
# evel表示上下旋转的角度
# azim表示平行旋转的角度
def plot_3D(elev=30,azim=30,x=x,y=y):
    ax=plt.subplot(projection="3d")
    ax.scatter3D(x[:,0],x[:,1],r,c=y,s=50,cmap="rainbow")
    ax.view_init(elev=elev,azim=azim)
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    ax.set_zlabel("r")
    plt.show()
plot_3D()

此时我们的数据在三维空间中，我们的超平面就是一个二维平面。明显我们可以用一个平面将两类数据隔开，这个平面就是我们的超平面。我们刚才做的，计算r ，并将 r 作为数据的第三维度来讲数据升维的过程，被称为 “ 核变换” ，即是将数据投影到高维空间中，以寻找能够将数据完美分割的超平面，而在高维空间中计算来找出超平面的函数就叫做核函数。在SVM 中，这个功能由参数 “kernel”控制。在这里我们使用的是 “linear" ，线性核函数，只能用于线性的情况。刚才我们使用的计算 r 的方法，其实是高斯径向基核函数，在参数”kernel“ 中输入 ”rbf“ 就可以使用。我们来看看模型找出的决策边界时什么样：

clf=SVC(kernel="rbf").fit(x,y)
plt.scatter(x[:,0],x[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)

3. SVC的重要参数kernel

3.1 在sklearn中实现SVC的基本流程：

from sklearn.svm import SVC #导入需要的模块
clf = SVC()     #实例化
clf = clf.fit(X_train,y_train) #用训练集数据训练模型
result = clf.score(X_test,y_test) #导入测试集，从接口中调用需要的信息

3.2 kernel

作为 SVC 类最重要的参数之一， “kernel" 在 sklearn 中可选以下几种选项：

输入	含义	解决问题	参数gamma	参数degree	参数coef0
"linear"	线性核	线性	no	no	no
"poly"	多项式核	偏线性	yes	yes	yes
"sigmoid"	双曲正切核	非线性	yes	no	yes
"rbf"	高斯径向基	偏非线性	yes	no	no

3.3 月亮型、环型、簇型、分类型在4个核函数不同的表现

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import svm
from sklearn.datasets import make_circles, make_moons, make_blobs,make_classification
n_samples = 100
datasets = [
    make_moons(n_samples=n_samples, noise=0.2, random_state=0),
    make_circles(n_samples=n_samples, noise=0.2, factor=0.5, random_state=1),
    make_blobs(n_samples=n_samples, centers=2, random_state=5),
    make_classification(n_samples=n_samples,n_features = 
2,n_informative=2,n_redundant=0, random_state=5)
 ]
Kernel = ["linear","poly","rbf","sigmoid"] 
for X,Y in datasets:
    plt.figure(figsize=(5,4))
    plt.scatter(X[:,0],X[:,1],c=Y,s=50,cmap="rainbow")

# 构建子图
nrows=len(datasets)
ncols=len(kernel)+1
fig,axes=plt.subplots(nrows,ncols,figsize=(20,16))
# 第一层循环：在不同的数据集中循环
for ds_cnt,(x,y) in enumerate(datasets):
    #在图像的第一列，放置原数据的分布
    ax=axes[ds_cnt,0]
    if ds_cnt==0:
        ax.set_title("Input Data")
    ax.scatter(x[:,0],x[:,1],c=y,zorder=10,cmap=plt.cm.Paired,edgecolors="k") #zorder越大，图像显示越上面
    ax.set_xticks(())
    ax.set_yticks(())
    #第二层循环：在不同的核函数中循环
    #从图像的第二列开始，一个个填充分类结果
    for est_idx,kernel in enumerate(kernel):
        #定义子图位置
        ax=axes[ds_cnt,est_idx + 1]
        clf=svm.SVC(kernel=kernel,gamma=2).fit(x,y)
        score=clf.score(x,y)
        #绘制图像本身分布的散点图
        ax.scatter(x[:,0],x[:,1],c=y
                  ,zorder=10
                  ,cmap=plt.cm.Paired
                  ,edgecolors='k')
        #绘制支持向量
        ax.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=50,
                  facecolors='none',zorder=10,edgecolors='k')
        #绘制决策边界
        x_min,x_max=x[:,0].min()-0.5,x[:,0].max()+0.5
        y_min,y_max=x[:,1].min()-0.5,x[:,1].max()+0.5
        #步长是复数，则其整数部分就是起始值和结束值之间创建的点的数量，并且结束值被包含在内
        XX,YY=np.mgrid[x_min:x_max:200j,y_min:y_max:200j]
        #np.c_类似于np.vstack的功能
        Z=clf.decision_function(np.c_[XX.ravel(),YY.ravel()]).reshape(XX.shape)
        #填充等高线不同区域的颜色
        ax.pcolormesh(XX,YY,Z>0,cmap=plt.cm.Paired)
        #绘制等高线
        ax.contour(XX,YY,Z,colors=['k','k','k'],linestyles=['--','-','--'],levels=[-1,0,1])
        
        ax.set_xticks(())
        ax.set_yticks(())
        
        #将标题放在第一行的顶上
        if ds_cnt==0:
            ax.set_title(kernel)
            
        #为每张图添加分类的分数
        ax.text(0.95,0.06,('%.2f'%score).lstrip('0')
                ,size=15
                ,bbox=dict(boxstyle='round',alpha=0.8,facecolor='white')
                #为分数添加一个白色的格子作为底色
                ,transform=ax.transAxes #确定文字所对应的坐标轴，就是ax子图的坐标轴本身
                ,horizontalalignment='right' #位于坐标轴的什么方向
               )
plt.tight_layout()
plt.show()

可以观察到，线性核函数和多项式核函数在非线性数据上表现会浮动，如果数据相对线性可分，则表现不错，如果是像环形数据那样彻底不可分的，则表现糟糕。在线性数据集上，线性核函数和多项式核函数即便有扰动项也可以表现不错，可见多项式核函数是虽然也可以处理非线性情况，但更偏向于线性的功能。

Sigmoid核函数就比较尴尬了，它在非线性数据上强于两个线性核函数，但效果明显不如rbf，它在线性数据上完全比不上线性的核函数们，对扰动项的抵抗也比较弱，所以它功能比较弱小，很少被用到。

rbf，高斯径向基核函数基本在任何数据集上都表现不错，属于比较万能的核函数。我个人的经验是，无论如何先试试看高斯径向基核函数，它适用于核转换到很高的空间的情况，在各种情况下往往效果都很不错，如果rbf 效果不好，那我们再试试看其他的核函数。另外，多项式核函数多被用于图像处理之中。