凸优化简单梳理

凸集

定义：集合C内任意两点间的线段均在集合C内，则称集合C为凸集，即:

然后拓展到K个点即：

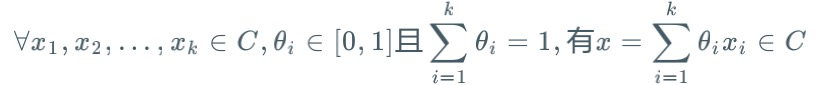
例如：

超平面、半空间、多面体

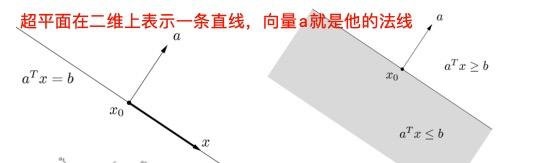
超平面hyperplane: {x ∣ a^T x = b}
如果向量a乘以X等于b,则这个表达的任意的x就代表超平面。
如果将等号变为大于等于或者小于等于，则这个任意的x就代表超平面所确定的半空间。
半平面(半空间)halfspace: {x ∣ a^T x ≤ b} ，{x ∣ a^T x ≥ b}

多面体：有限个半空间和超平面的交集。

事实上放射集（超平面、直线）、射线、线段、半空间都是广义上的多面体。
显然多面体是凸集。

分割超平面

设C和D为两不相交的凸集，则存在超平面P，P可以将C和D分离。

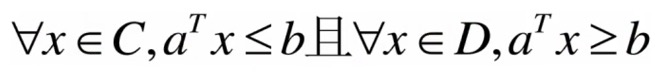
分割超平面的构造：
两个集合的距离，定义为两个集合间元素的最短距离。然后做集合C和集合D最短线段的垂直平分线。

支撑超平面

设集合C，x₀为C边界上的点。若存在a≠0,满足对任意x∈C，都有a^Tx≤a^Tx₀,成立，则称超平面{xIa^Tx=a^Tx₀}为集合C在点x₀处的支撑超平面。
凸集边界上任意一点，均存在支撑超平面。反之，若一个闭的非中空(内部点不为空)集合，在边界上的任意一点存在支撑超平面,则该集合为凸集。

凸函数

记得高数上的凸函数判断方法是: f((x₁+x₂)/2 ≤ (f(x₁)+f(x₂))/2成立
现在有一种定义方法：

这个定义看图之后一目了然：

一阶可微

结合凸函数图像和支撑超平面理解，对于凸函数，其一阶Taylor近似本质上是该函数的全局下估计。反之，如果一个函数的一阶Taylor近似总是起全局下估计，则该函数是凸函数。
该不等式说明从一个函数的局部信息，可以得到一定程度的全局信息。

二阶可微

若函数f二阶可微，则函数f为凸函数当前仅当dom为凸集，且

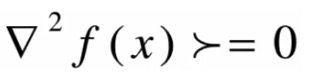
若f是一元函数，上式表示二阶导大于等于0
若f是多元函数，上式表示二阶导Hessian矩阵半正定。

凸函数的性质

性质1: 设f (x)为定义在凸集S上的凸函数，则对任意实数β > 0 ， 函数βf (x)也是定义在凸集S上的凸函数。

性质2: 设f1 (x)和f2 (x)都是定义在凸集S上的凸函数，则函数 f1 (x) + f2 (x)也是定义在凸集S上的凸函数。

性质3: 设f (x)为定义在凸集S上的凸函数，则对任意实数β，集合 S_β = {x∣x ∈ S, f (x) ≤ β}是凸集。

性质4: 设f (x)为定义在凸集S上的凸函数，则f (x)的任一个极小点就是它在S上的全局极小点，而且所有极小点的集合是凸集。

凸优化

优化问题的基本形式

minimize : f₀(x)， x∈Rⁿ
subject to : f_i(x)≤0， i=.,…,m
h_j(x)=0， j=…p
优化变量 x∈Rⁿ
不等式约束f_i(x)≤0
等式约束 h_j(x)=0.
无约束优化 m= p=0

凸优化问题的基本形式

minimize : f₀(x)， x∈Rⁿ
subject to :
f_i(x)≤0， i=.,…,m
h_j(x)=0， j=…p

f_i(x)(0≤i≤m)为凸函数，h_j(x)(1≤i ≤p)为仿射函数

凸优化问题的重要性质:可行域为凸集;局部最优解即为全局最优解

举个例子

要用薄钢板制造一体积为5m³的无盖货箱，由于运输装载要求， 其长度不小于4m。问: 长、宽、高维多少用料最省？

解:分析可知，钢板的耗费量与货箱的表面积成正比。设货箱的长、宽、高分别为X1,X2,X3，货箱的表面积为S,则该问题的物理表达式为:
(1)货箱的钢板耗费量(即货箱的表面积用料)最少:
S=x1x2 + 2(x1x3 + x2x3)→min
可见货箱的表面积取决于货箱的长度X1宽度x2和高度x3。
(2)满足的条件: x≥4;x2≥0;x3≥0
按优化数学模型的规范形式，可归纳为如下数学模型:

设计变量:X=[x1 x2 x3]^T
目标函数的极小化: min f(X)= S = x1x2 +2(x1x3 + x2x3)
约束条件:
g1(X)=4-x1≤0
g2(X)=-x2≤0
g3(X)=-x3≤0
h(X)=5- x1x2x3=0
由等式约束条件可知，三个设计变量中只有两个是独立变量，即x3 =5/x1x2
所以，该问题的优化数学模型应写为:
设计变量: X=[x1 x2]^T
目标函数的极小化: min f(X)=x1x2 +2(x1x3 + x2x3)=x1x2 +10(1/x1 + 1/x2)
约束条件:
g1(X)=4-x1≤0
g2(X)=-x2≤0
h(X)=5- x1x2x3=0
这样使该优化问题的数学模型更为准确、精炼

对偶问题

对于一般优化问题构造拉格朗日函数：
minimize : f₀(x)， x∈Rⁿ
subject to :
f_i(x)≤0， i=.,…,m
h_j(x)=0， j=…p

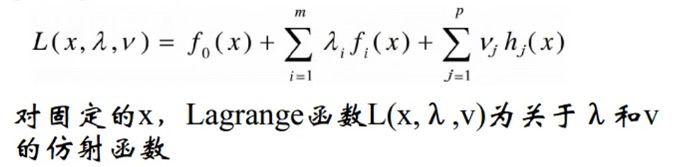
鞍点

为表述方便，假设没有等式约束，只考虑不等式约束，结论可方便的扩展到等式约束。
假设x0不可行,即存在某些i，使得f_i(x)>0。则选择λ_i→∞,对于其他乘子λ_j=0,j≠i ,假设x0可行，则有f_i(x)≤0,(i=1,2,m),选择λ_i=0,i= 1,…,m 有:

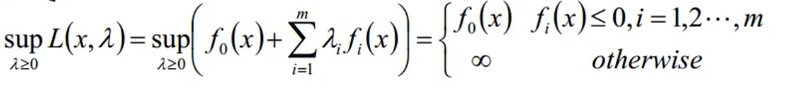
最优点

原问题是求f₀(x)的下确界 inf f₀(x)，本质也就是对拉格朗日函数先求上确界再求下确界：

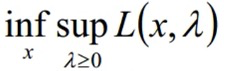
而对偶问题是求对偶函数的最大值即：

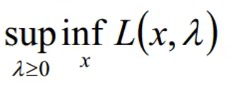
但是：

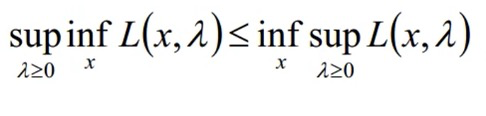
关于上面不等式的证明如下：
定义域内任意的 x，y都有：

强对偶条件

若要对偶函数的最大值即为原问题的最小值，考察需要满足的条件:

所以要取等号的话需要满足

这就是KKT条件。