中心化、本地化差分隐私基础知识

差分隐私的背景和概念

由于互联网的发展，包括智能手机在内的各种终端数量剧烈的增长，使得各种公司和组织，以及政府需要收集和分析巨量的数据。在这个过程中，关于个人信息的隐私保护成为了一个大的问题。一些在大数据环境下的隐私保护方案，包括k-匿名技术，在需要发布用户数据的情况下，k-匿名可以较为有效地保护个人的隐私不被泄露。因为其可以保证具有相同敏感属性的等价类中，至少具有K个记录，这样攻击者便无法分辨某一用户具体是哪一条记录。然而，k-匿名还是无法阻止一些攻击，无法提供数学可证明的安全性。在同质攻击的场景下，由于k条记录中敏感值相同，无法阻止攻击者获取某用户的隐私信息。或者在攻击者已知某用户的一些背景的信息情况下，则其可以推断某用户的敏感信息。

而在差分隐私的场景下，任何一条信息的增减，都不会影响最终的查询结果，因此，对于攻击者具备的知识并不关心。差分隐私可以提供一种可证明的量化方法，来保护个人的隐私数据，同时向数据发布和分析者提供限制条件下相对准确的数据。一方面，差分隐私可以按照隐私预算向用户提供隐私保护性，但是根据差分隐私算法可证明的性质，又可以提供对应的数据可用性，这都是形式化可证明的。

差分隐私技术可以分为两类，在传统应用场景下，需要一个数据中心来收集和发布分析数据，称为中心化的差分隐私，而如果在本地处理隐私数据，则称为本地化的差分隐私。对于本地化的差分隐私，由于近年来各种终端设备的疯狂增长，和这些设备算力的提高，本地差分隐私成为了一个热门的方向。这也获得了一些实际的应用，例如在苹果设备和谷歌的浏览器上。

中心化差分隐私

理解差分隐私的一个点在于理解，差分隐私是通过向查询结果中添加一个随机噪声来保护隐私的，这个噪声是一个随机变量，服从某种分布。 这样子，攻击者只有在很多次查询数据的情况下，通过统计随机变量的分布，来推断隐私信息，但是实际上攻击者无法不受限制地去查询信息。实际上，查询信息需要消耗隐私预算，通过有限的隐私预算来阻止攻击者通过查询结果的概率分布来推断信息。
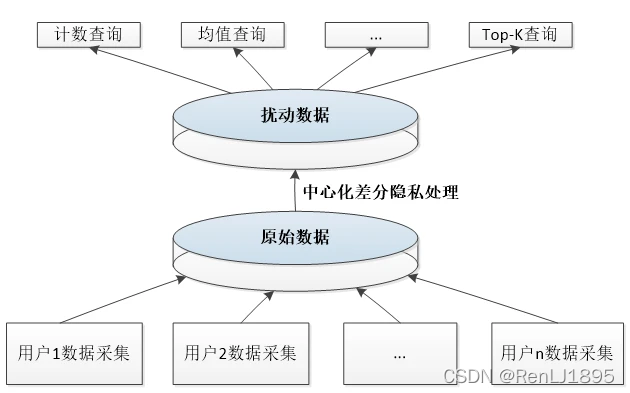
在这里插入图片描述

在不使用差分隐私的情况下，攻击者如何获取隐私信息呢？对于某一个数据集，攻击者先查询其统计量，例如未婚人群的个数，然后再查询某人的数据加入到这个数据集之后的统计量，此时，可以根据统计量的变化情况，来准确推断这个人的敏感信息。因此，可以看出，差分隐私中的“差分”，即为两个相邻的数据集的意味，而差分隐私就是要使得攻击者无法分辨这两个数据集，从而保护这两个数据之间的“差”的私密性，即某用户的数据。

下面先看传统的中心化差分隐私，在这种情况下，中心化的数据收集者拥有一个集中管理的数据集，然后发布这个数据集的统计量，他需要完成其中的隐私保护工作。

$\epsilon$ -差分隐私

设 $x$ 和 $x^{'}$ 是两个相邻的数据集，即它们之间差了一条数据，设 $\mathcal{M}:x\mapsto y$ 是随机化的机制，即查询结果为 $y=\mathcal{M}(x)$ ，那么可以这样子表示两个查询结果之间的距离：

$D_{\infty}=\max\limits_{y}\ln\frac{Pr(\mathcal{M}(x)=y)}{Pr(\mathcal{M}(x')=y)} \tag{1}$

这相当于对于某个输出，两个相邻数据集的查询结果为这个输出的最大概率差，实际上，这个式子可以认为是来源于KL散度的定义。如果令 $D_{\infty}<\epsilon$ ，再将上式通过指数运算消去，对于任意的输出集合 $S$ ，则可以得到 $\epsilon$ -隐私保护的定义：
$Pr(\mathcal{M}(x)\in S)<e^{\epsilon}Pr(\mathcal{M}(x')\in S) \tag{2}$

这样子就可以更为方便地理解隐私保护的定义，对于松弛版本的 $\epsilon$ 隐私保护，其定义为：
$Pr(\mathcal{M}(x)\in S)<e^{\epsilon}Pr(\mathcal{M}(x')\in S)-\delta \tag{3}$

同样可以通过变换理解为式(1)的情况：

$D_{\infty}=\max\limits_{y}\ln\frac{Pr(\mathcal{M}(x)=y)-\delta}{Pr(\mathcal{M}(x')=y)} \tag{4}$

即，两个相邻数据集的输出分布之间，同一个输出值之间的概率差距，最多可以允许为 $\epsilon-\delta$ 。

在这里，可以把式2中出现的 $\epsilon$ 定义为隐私预算，如果 $\epsilon$ 越小，说明算法对相邻数据集给出的分布越接近，这说明算法提供的隐私保护越强。对于隐私预算，其具有两个典型的性质，分别为串行和并行组合特性。

隐私预算的串行和并行性质

对于一系列隐私算法 $\mathcal{M}_1,\mathcal{M}_2,\cdots,\mathcal{M}_m$ ，他们给出的输出是两两独立的，则对于数据集 $x$ 而言，如果从1到m串行，即顺序使用这m个算法，则其提供 $m\epsilon$ -差分隐私。

而如果对于数据集的每个不相交的m个子集，分别使用这m个算法，则其提供 $\max(\epsilon,\cdots,\epsilon_m)$ -差分隐私。

在这m个算法互相独立的假设之下，这两个性质可以得到保证。

拉普拉斯和指数机制

下面是两个典型的传统差分隐私的扰动机制，适用于中心化的数据收集工作。

全局敏感度与拉普拉斯机制

如果是数据收集者负责扰动数据，则其需要根据数据集给出一个查询结果，设这个查询结果 $\eta$ 来自于某函数 $f:x\mapsto \eta$ ，则我们需要知道，在任意两个相邻数据集上，这个函数给出的最大差别，设这个差别为：

$\Delta f=\max_{x,x'}|f(x)-f(x')|_1 \tag{5}$

称这个量为敏感度（全局敏感度），这个概念在中心化差分隐私中很重要。采用不同的查询函数，其敏感度不同，但是我们希望可以在向这个查询结果添加扰动的时候，控制扰动的强度，因为我们需要去定量地平衡隐私性和数据可用性。

首先来看连续的数据类型，典型的扰动机制是拉普拉斯机制，即使用拉普拉斯分布采样扰动：

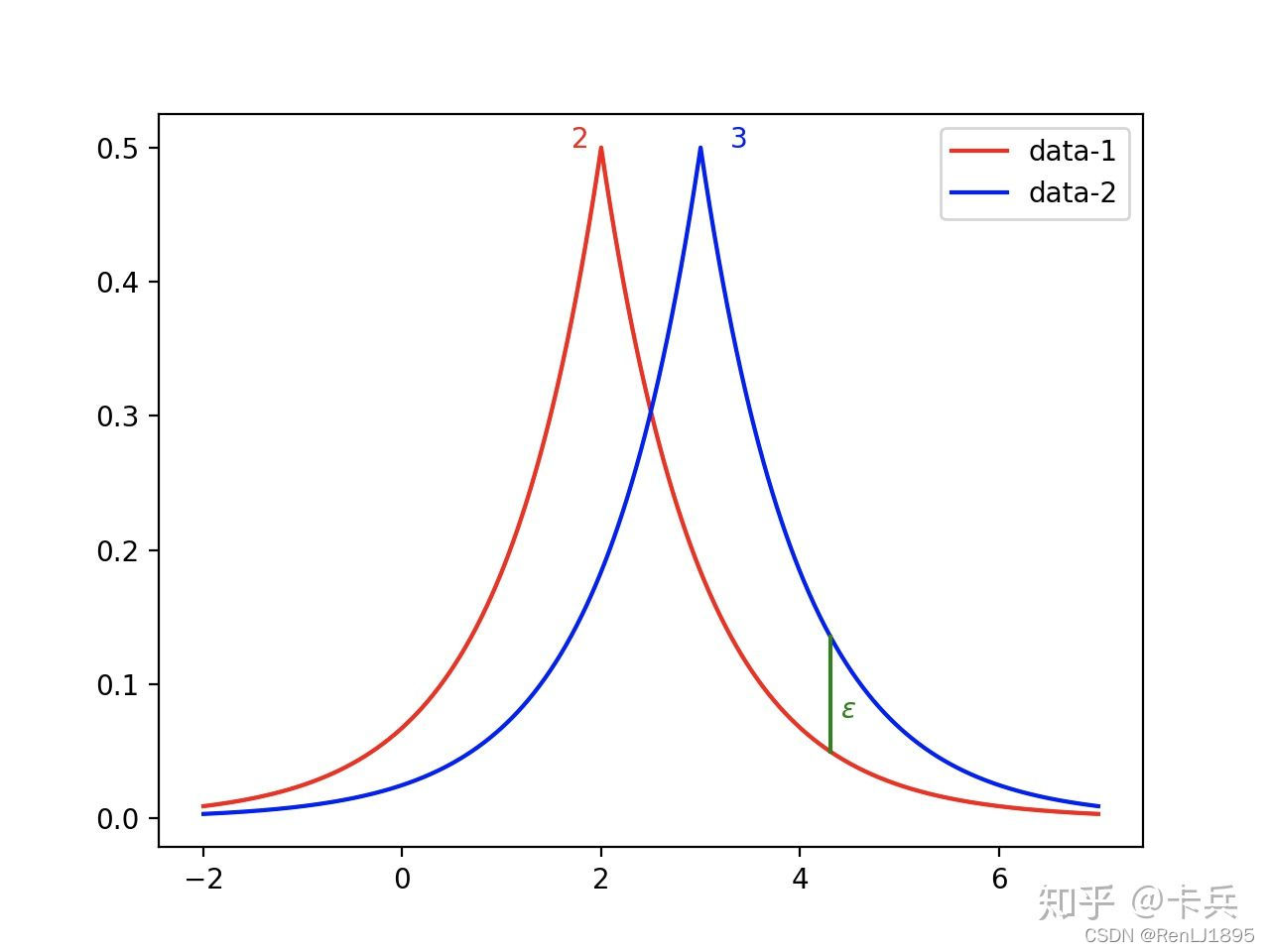
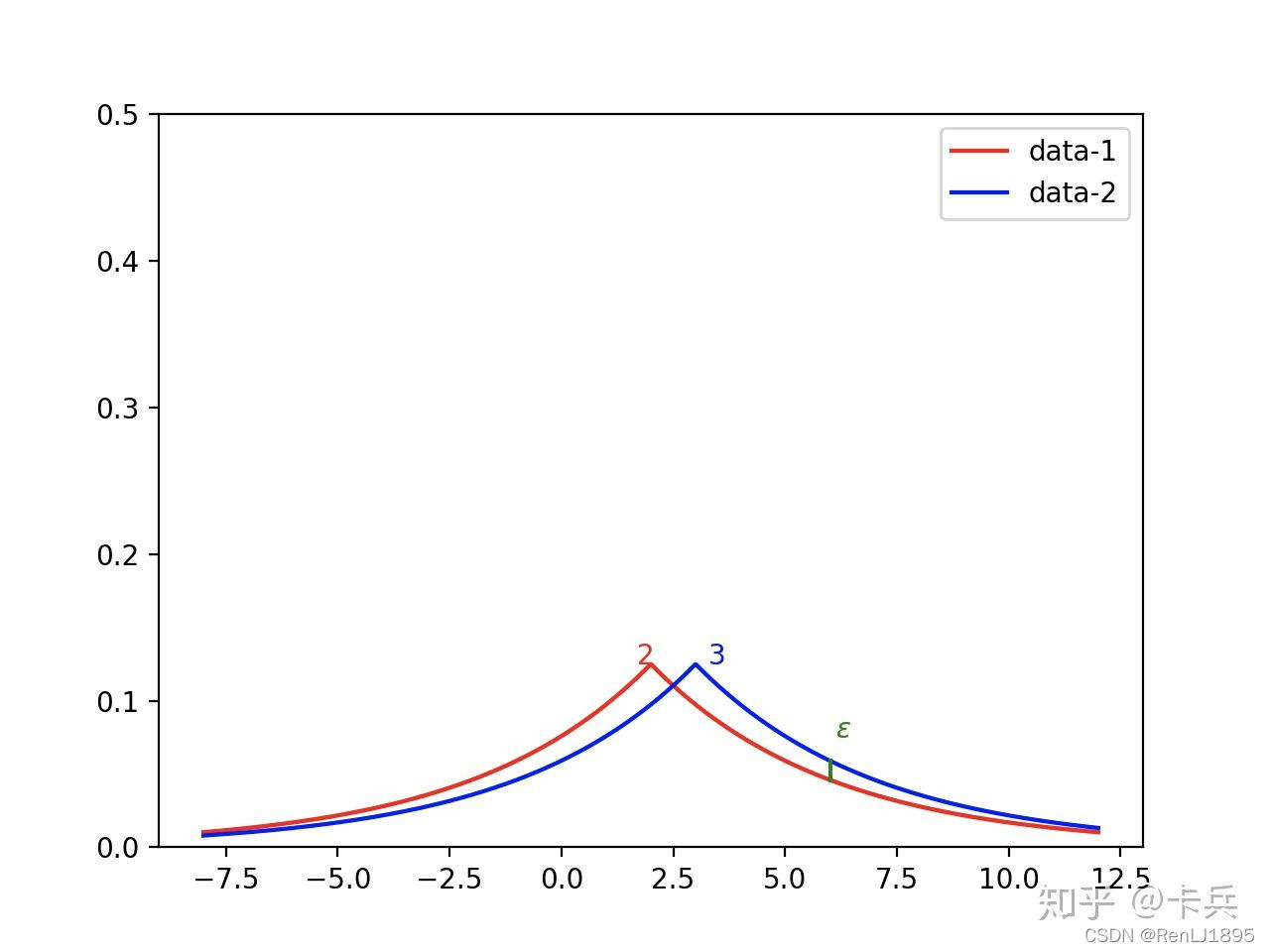
$\mathcal{M}(x)=f(x)+Lap(\frac{\Delta f}{\epsilon}) \tag{6}$
可以看到，如果查询函数的敏感度越大，说明查询函数越容易暴露信息，因此需要越强的扰动来保证隐私不泄露，对于拉普拉斯分布而言，就是将查询函数的敏感度放在分子部分。同时，也可以看出，如果隐私预算越大，则给出的扰动就越小，说明与真实数据接近的概率就越大，则越难保护隐私。
请添加图片描述

离散型数据与打分函数

而如果输出需要是离散的数据类型，例如类别，则无法简单地通过添加一个连续的数值来扰动，因为这会改变数据类型，而导致数据不可用。离散的查询结果，在返回查询结果的时候，是通过随机给出一个离散数据来实现的，例如如果是10个类别，则随机给出一个类别返回给查询者。因此，需要一个机制来给出不同类别的概率，然后数据的收集者依据不同类别的概率，依概率输出，概率越高的类别，被返回给查询者的概率越大。实现的时候不一定非要用概率来实现，只需要有一个值来表示不同输出结果的输出可能性就行了。

因此，这里引入一个打分函数 $q:x,\phi_i \mapsto s$ ，其中是 $\phi_i$ 其中一种输出结果，是一个离散的数据类型，例如一种类别，而 $s$ 是这个输出结果的分数，分数越高其被选中最终输出的概率就越高。打分函数具体的设计依赖具体的任务类型，需要应用的设计者亲自设计。直观上，对于真实的输出结果，其分数应该越高，而越接近这个真实输出的其他输出结果，其概率相应地也应该比其他的输出结果高，这样才能保证隐私性的同时，提供可用性。

下面就可以定义指数机制了：

$\mathcal{M}(x)=f(x)=\phi_i \quad w.p.\propto exp({\frac{\epsilon q(x,\phi_i)}{2\Delta q}}) \tag{7}$

注意这里的打分函数 $q$ 同样可以定义一个敏感度，含义与查询函数的敏感度相同。这里的指数函数与上面的拉普拉斯分布不同，试想对于给定的两个不同的分数 $ks_1,ks_2,k>0$ ，如果k越大，由于这里是指数函数，则两个分数之间的差距越大，则分数高的越有可能被输出，则隐私越可能被泄露。因此，如果想要提供比较强的隐私保护，则需要使得最后给出的不同输出结果的输出可能性更加接近，也就是使得这个k变小。因此，和拉普拉斯机制同样的原理，如果打分函数的敏感度越高，说明对于同一个输出结果，两个相邻数据集之间的分数差别越大，因此这里将其放在分母，来平衡这种影响。

这就是中心化差分隐私的情况下，满足 $\epsilon$ -差分隐私下的拉普拉斯和指数机制，分别针对连续和离散的数据类型。在中心化差分隐私的定义和扰动中，相邻数据集 $x$ 和 $x^{'}$ 的概念非常重要。

本地化差分隐私

与中心化差分隐私相比，本地化差分隐私最大的特点在于，其不需要预设一个可信的第三方数据收集者，而是由每个用户将其脱敏过后的“真实”数据发送给数据收集者，这可以保证不会透露隐私信息。所以其与中心化的传统差分隐私的核心区别就是将数据扰动的工作从数据收集方移到了数据提供方，这对差分隐私算法提供了新的要求。在现在这个移动智能设备遍地的时代，移动设备具有不错的性能，加之用户的隐私保护要求也越来越高，本地化的差分隐私成为了一种很重要的技术。而且可以想见，由于大数据时代用户隐私数据具有各种各样的多样性，例如结构化的数据，具有相关性的键值数据等等。
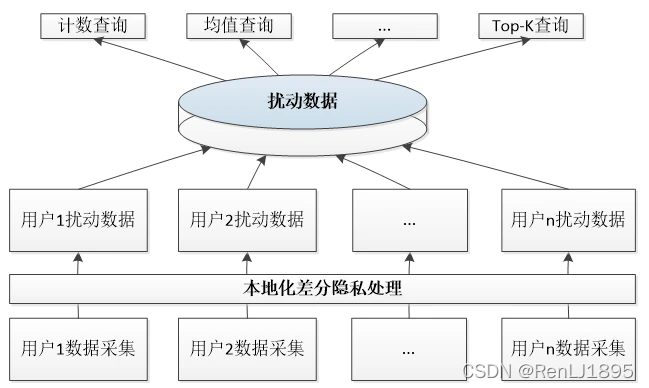
在这里插入图片描述

本地化差分隐私的定义如下，注意其与中心化差分隐私的不同：

给定n个用户，每个用户拥有一条记录，和是两个用户的不同的两个记录，如果算法在这两条记录上给出相同输出结果的可能性满足如下不等式，则说明其满足-本地化差分隐私。
$Pr[\mathcal{M}(t)=t^*]\le e^{\epsilon}\times Pr[\mathcal{M}(t')=t^*] \tag{8}$

中心化、本地化差分隐私的异同

与中心化差分隐私不同，在本地化差分隐私这里，用户之间并不能知道互相之间的记录，也没有一个中心化的数据收集者，因此不存在相邻数据集这种概念。因此这里其实是将两个相邻数据集替换成了两条来自不同用户的不同记录，从使得攻击者无法分别两个相差一条记录的数据集，变成了使得攻击者（很可能就是数据收集者）无法分辨来自两个用户的记录的异同。

这里使得中心化差分隐私和本地化差分隐私具有一点异同，就是关于数据统计量的要求。对于中心化差分隐私，其可以通过定义式(5)的全局敏感性，来定量地去限制扰动地强度，来保证数据的可用性。而对于本地化的差分隐私，则需要通过大量的数据量来抵消噪声的影响，从而保证最后得到的数据的可用性，从下面随机响应的例子式(9)和式(13)中可以看出这一点。

对于本地化的差分隐私，同样也具有串行和并行的组合性质，这一点与中心化的差分隐私相同。对于串行组合性，其强调的是对数据的不同步骤的处理，其隐私预算满足的性质；而对于并行组合型，则是强调的将数据集分为不相交的子集来处理的时候，总的算法的隐私预算满足的性质。对于中心化和本地化的差分隐私，由于只是从相邻数据集转移到了两个用户之间的数据，而并没有改变隐私预算保证的形式，所以本地化的差分隐私继承了这两点性质。

随机响应技术

可以从一个简单的案例来理解如何通过在本地扰动收集到的个人信息来进行隐私保护，在这种情况下，数据收集者无法获知个人的敏感信息，同时也能得到一个相对准确的统计值。

一个简单的随机响应例子

例如，统计某人群的敏感信息，如婚姻状况，分为“未婚”和“已婚”，设一共有n个人，我们需要知道这个人群中未婚人群的个数 $\pi$ 。在提问者回答问题的时候，其通过某随机机制决定是否回答真实信息，假设其真实回答的概率为p。如果最后的统计结果是回答“未婚”的人有m个，则数据收集者最后得到的未婚人个数的似然函数为：

$L=(\pi p+(1-\pi)(1-p))^m((1-\pi)p+\pi(1-p))^{n-m} \tag{9}$
于是可以求出其极大似然，然后便可以得到“真实”的值：

$\hat{\pi}=(\frac{p-1}{2p-1}+\frac{m}{(2p-1)n})n \tag{10}$

在这一个案例中，从差分隐私的定义的角度考虑，任意两个相邻数据集，对于其中一个数据集的任意输出，其可能有两种输出，分别为“是”和“否”，则可以认为式1中输出情况最大概率距离即为两种情况的比值，于是可以认为 $\epsilon$ -差分隐私中的 $\epsilon$ 即为：
$\epsilon=\ln\frac{p}{1-p} \tag{11}$

上面的例子是一个简单的扰动机制，只能对二值的离散数据适用。

改进到多类型、连续型数据的思路

可以将上面的技术改进以适应多值的离散型数据，可以有两种改进的思路，分别从数据和算法的角度考虑。

如果从数据的角度考虑，对于每个用户的数据，其有k种取值，且k大于2，则可以将其编码为长度为 $\lceil \log k \rceil$ 的二进制串，这样，对于每种取值，其对应于一个二进制串，且长度相同。在扰动的时候，可以对每个bit分别扰动。问题在于k不一定可以表示为2的指数形式，这可能会在随机响应的误差之外又带来误差。而如果从改进算法使其能适应任意k取值的角度考虑，则是将原来的对于两种情况的概率分配修改为能够覆盖k种情况。

Harmony算法

对于连续的数据类型的随机响应，可以通过将连续值离散化的方法实现。在PrivKV的论文中就应用了这种思路，其是使用了一种改进的Harmony算法，可以将连续的-1到1之间的值，离散化为-1和1，然后数据收集者可以通过大量的数据量得到一个连续的值，从而保证了可用性。

例如用户 $u_i$ 具有一个数据 $v\in [-1,1]$ ，其分配的隐私预算为 $\epsilon$ ，则Harmony算法可以分为下面几步。

首先将待输出的扰动结果初始化为
$v^*=0$
然后按下式子赋值：

$v^*=\begin{cases} 1, \quad w.p.\quad \frac{1+v}{2}\\ -1, \quad w.p.\quad \frac{1-v}{2} \end{cases}$

然后根据隐私预算做下面的扰动：

$v^*=\begin{cases} 1, \quad w.p.\quad \frac{e^{\epsilon}}{1+e^{\epsilon}}\\ -1, \quad w.p.\quad \frac{1}{1+e^{\epsilon}} \end{cases} \tag{12}$

这样子，就将连续的值，离散化为了离散的值，返回给数据收集者。设想做n次随机响应，其中得到1的次数为m，然后可以写出这种情况下，最后得到 $v$ 值的估计 $v^*=(m-(n-m))/n$ 的似然函数如下：
$L=(\frac{1+v_j}{2}\cdot\frac{e^{\epsilon}}{1+e^{\epsilon}}+\frac{1-v}{2}\cdot\frac{1}{1+e^{\epsilon}})^m \cdot(\frac{1-v_j}{2}\cdot\frac{e^{\epsilon}}{1+e^{\epsilon}}+\frac{1+v}{2}\cdot\frac{1}{1+e^{\epsilon}})^{n-m} \tag{13}$

可以求出，这不是一个无偏的估计，所以最后，需要对这个随机变量做校准，以使得其是真实值的无偏估计：
$v^*=v^*\cdot\frac{e^{\epsilon}+1}{e^{\epsilon}-1} \tag{14}$

中心化、本地化差分隐私基础知识

差分隐私的背景和概念