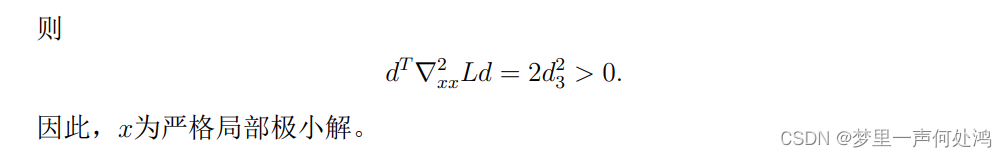高等工程数学 —— 第五章 （2）非线性规划的最优条件

高等工程数学 —— 第五章 （2）非线性规划的最优条件

无约束规划问题的最优性条件

简单说就是先用一阶必要条件求驻点，再用二阶充分条件来验证。

• 其实就是一阶导数为0然后解未知量的值

这里的Hesse矩阵如下：

再简单说说判断矩阵是否正定的两种方法：

1. 求出A的所有特征值。若A的特征值均为正数，则A是正定的；若A的特征值均为负数，则A为负定的。
2. 计算A的各阶顺序主子式。若A的各阶顺序主子式均大于零，则A是正定的；若A的各阶主子式中，奇数阶主子式为负，偶数阶为正，则A为负定的。

例如：

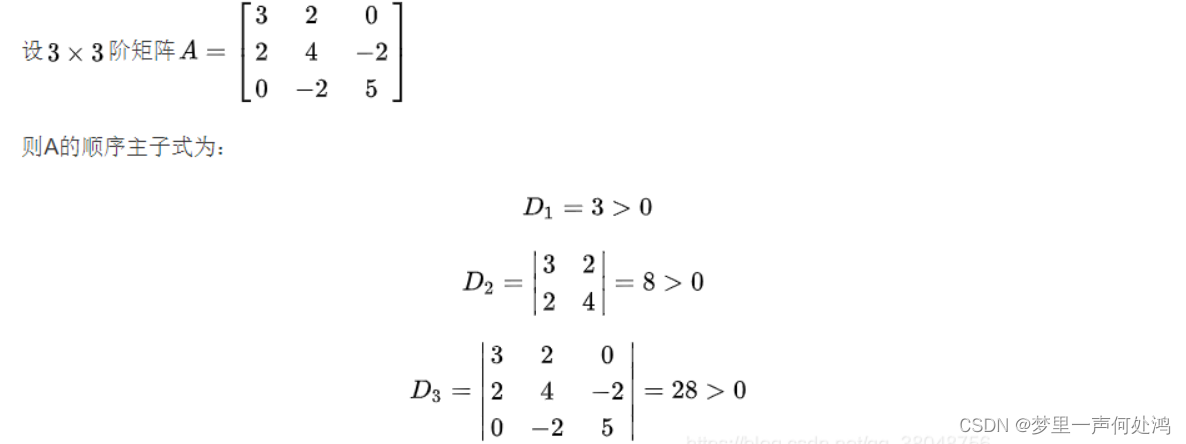
• 可知矩阵$A$是正定矩阵

用一道例题就能很容易的理解：

• 可见这里我们用一阶必要条件求出来了两个驻点

• 这里我们用二阶充分条件来判断出第一个驻点代入Hesse矩阵不正定，所以可知第二个驻点是严格局部极小值点

带约束规划问题的最优性条件

KKT

简单讲就是先用KKT必要条件求值，然后再用二阶充分条件来验证。

KKT必要条件

• 注意(5)式是对每一个$x$来就梯度，即求一阶导数

二阶充分条件

• 这里先求$d$然后判断(10)式是否满足大于0

例1：

• 我们用KKT必要条件列出的式子来求出未知数的值，接下来用二阶充分条件来验证

• 这里是用$v_j>0$那个式子来求$d$的

• 可见这里求得的值大于0，因此我们求得的点就是局部极小值点

例2：