Pytorch ——基础指北_贰
本文已参与「新人创作礼」活动.一起开启掘金创作之路。
软件环境:
配套代码下载地址:
gitee-pytorch
基础知识:
要想训练一个网络,对于梯度的理解是必不可少的,下面首先介绍梯度的一些基础概念。
0、方向余弦与向量单位化
方向余弦是一个在向量中很常见的概念,它用来标定某一个向量的方向,说起来可能会一头雾水,不过没关系,我们使用画图来理解一下。
举个例子,如下图有一个坐标系xoy,其效果如下所示:
其中包含了一个向量
l
,向量的坐标为:
(a,b)
那么上文中的向量就满足如下式子:
(a2+b2
a,a2+b2
b)
上文的式子实际上就是对向量进行单位化,此时新产生的向量,实际上就是我们常说的方向向量。
方向向量实际上还可以再优化一下,我们看到图上还有两个标明的角分别是
α和β,这两者的关系就不再多说,他们呢一对互余的角度,满足的条件就是相加等于90度。
此时我们就可以将这个式子转化成这样的形式:
a2+b2
a=cosα
同理也有:
a2+b2
b=cosβ
这样方向的向量的表达式,就可以写为:
(a2+b2
a,a2+b2
b)=(cosα,sinα)
实际因为角度互余上可以化为:
(cosα,cosβ)
1、多元函数求偏导
一元函数,即有一个自变量。类似
f(x)
多元函数,即有多个自变量。类似
f(x,y,z),三个自变量x,y,z
多元函数求偏导过程中:对某一个自变量求导,其他自变量当做常量即可
例1:
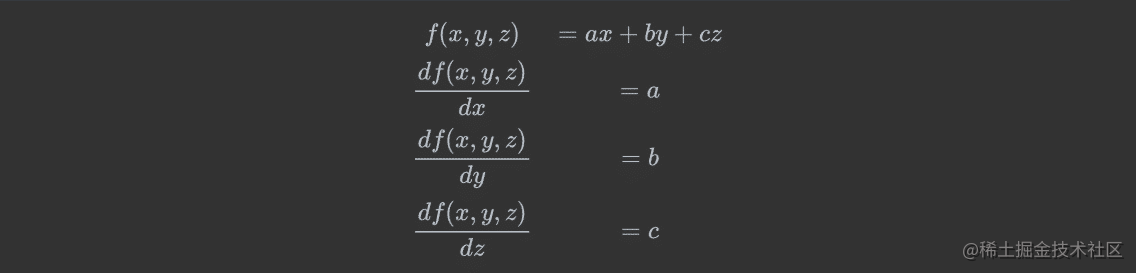
例2:
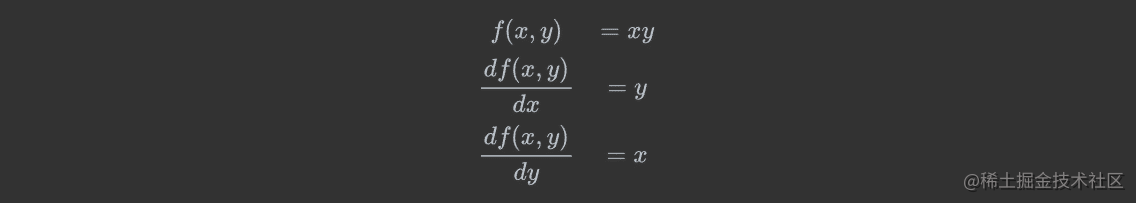
例3:
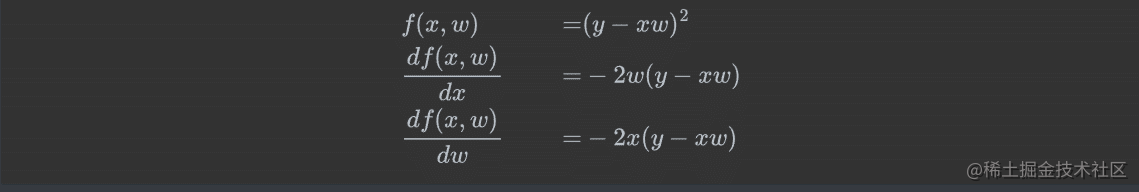
练习:
已知
J(a,b,c)=3(a+bc),令u=a+v,v=bc,求a,b,c各自的偏导数。
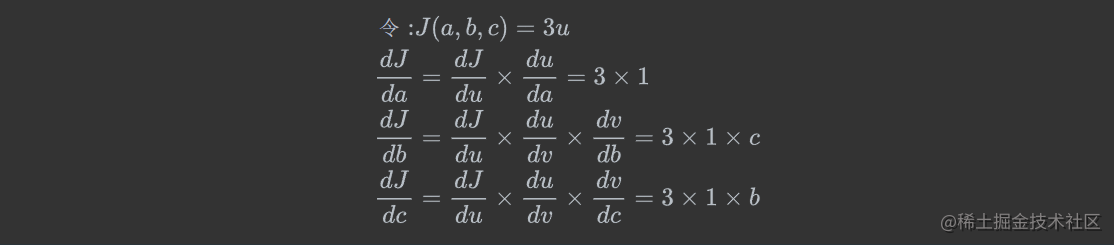
2、方向导数:
简单地说方向导数形容的是满足某个关系下(Y=KX+B),对于各个方向上本关系数值变化率(Y的变化率)的量化表达式。
数学推导,可参考如下文章。但是我读完以后还是没办法一下就理解,它实际上不应该是一个这么难理解的内容,我们反过来想一想,能不能从前面的基础构建出来方向导数到底是什么。
方向导数1 第一章
方向导数2
从二维、三维入手
在二维关系中Y=KX+B中我们不太好理解什么是方向导数,我们知道对于一个函数来说,
y=kx+b的导数实际上是这样的:
对于函数的某一点,导数等于切线在该点的斜率,他是一个极限概念。我们不妨这样来理解这个极限的过程:
下图是某个函数,其中包含三个点如下所示:
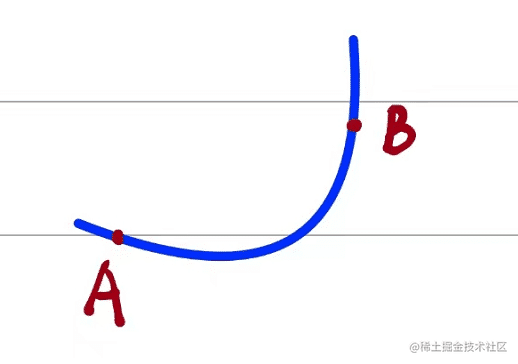
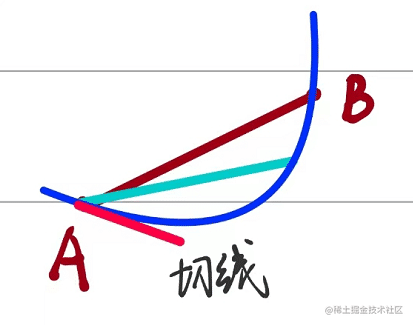
其中A、B是函数上随机的两个点。其中A、B两点满足如下:
A=(x0,f(x0))B=(x0+Δx,f(x0+Δ))
然后AB两点相连接,形成一个割线,割线的斜率满足如下条件:
kAB=(x0+Δx)−x0f(x0+Δx)−f(x0)=Δxf(x0+Δx)−f(x0)
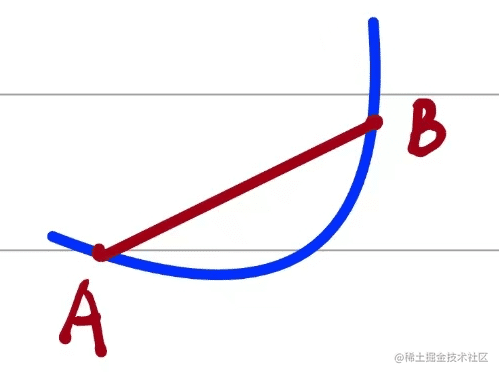
当有如下情况的时候,就会产生切线和导数:
当B无限趋近于A的时候,即
Δx无限趋近于0的时候,割线AB就会转化为切线,如下所示:
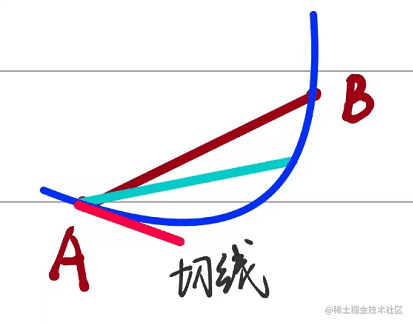
满足的数学关系如下:
kab=\varliminfΔx→0Δxf(x0+Δx)−f(x0)
而我们知道切线的斜率就是导数的值,这是在二维的情况下。
三维的方向导数
在二维的情况我们已经很了解了,我们来推广到到三维的情况下来试一试,举个例子:
我们先来下一个定义:
一般情况下的三位函数的方向导数实际上是平面XOY上一点
(x,y)在三维函数的值
f(x,y),和其所代表的一点
(x,y,f(x,y))以向量l的方向向量为切面构成的曲线上(点(x,y))的一条切线的值。
说起来很抽象,我们举个例子就好理解一点了:
其中三维函数圆形抛物面大致如下:
Z=x2+y2
如图所示:
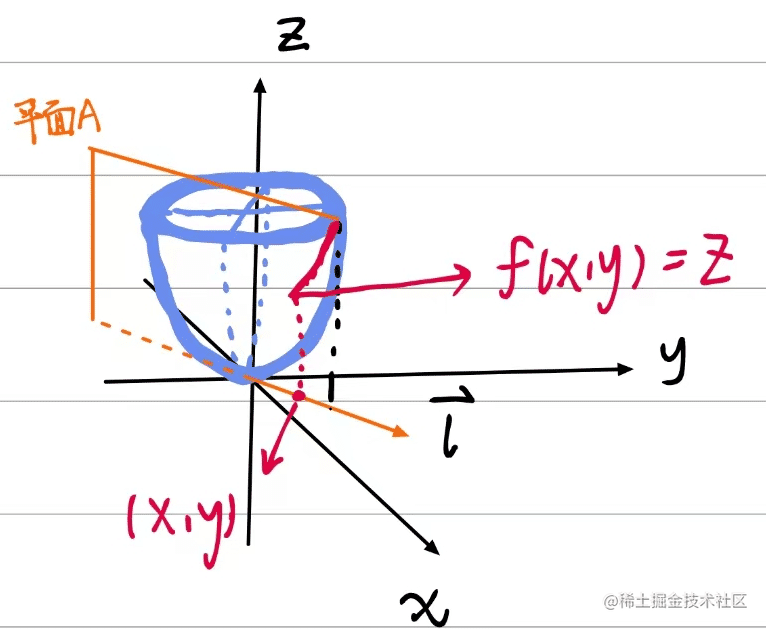
图看起来很很复杂不过没关系,我们依靠颜色来分辨一下:
红色包含两部分内容:分别是在xy平面的点
(x,y)和切面构成的曲线。
橙色包含两部分内容:
l
是
XOY 平面(笛卡尔坐标系)上以
P(X0,Y0)为始点的一条射线,
el=(cosα,cosβ) 是与 L 同方向的单位向量。同时还包含一个由其方向向量构建出来的平面A。
蓝色部分包含一个内容:就是函数Z。
我们来解析一下这分别什么意思
当存在一个点c从点(x,y)出发沿着方向向量变化
t的时候,其坐标满足如下:
C=(x+tcosα,y+tcosβ)(其中角度和上文中的是一样意义)
这时候c点实际上就是黑色虚线在l上的点。这时候这个在向量上的变化轨迹就是一段向量,他的方向和l向量的方向向量是一样的,并且在函数上映射了一段曲线,如红色部分曲线所示,我们针对这一种曲线来考虑一种特殊情况,当满足这个条件的时候,曲线会如何变化?
没错就是上文中二维的情况:
结果是一模一样的,只不过这里的切线是对应的在曲线上的切线,我们这里就引出方向导数的定义如下:
∂l∂f∣∣∣∣∣(x0,y0)=t→0+limtf(x0+tcosα,y0+tcosβ)−f(x0,y0)
从方向导数的定义可知,方向导数 ∂l∂f∣∣∣∣∣(x0,y0) 就是函数 f(x,y) 在点 P0(x0,y0) 处沿方向 l 的变化率.
定理:
如果函数 f(x,y) 在点 P0(x0,y0) 可微分,那么函数在该点沿任一方向 的方向导数存在,且有 :
∂l∂f∣∣∣∣∣(x0,y0)=fx(x0,y0)cosα+fy(x0,y0)cosβ注意里面为偏导实际上就分解成了XY轴上函数变化率
其中,
cosα 和 cosβ是向量
l 的方向余弦。
这里再说明一下方向导数和偏导数有什么区别呢?
偏导数实际上方向导数的特例,当向量取x的正轴的时候,此时方向导数就转变为了对于x的偏导数,推导如下:
∂l∂f∣∣∣∣∣(x0,y0)=t→0+limtf(x0+tcosα,y0)−f(x0,y0)
如果你仔细看就会发现实际上这里的定义就是偏导数的定义,也就说是方向导数的一种情况。
其次再说明一下,这个式子的意义在哪里:
∂l∂f∣∣∣∣∣(x0,y0)=fx(x0,y0)cosα+fy(x0,y0)cosβ
实际上,我们用来计算方向导数的时候就是使用这个式子,这个式子就是将对应的方向向量分解为x轴和y轴的方向余弦来进行计算,也就说方向向量实际上是由x轴和y轴的方向余弦构成的。
还有就是对于用同一个点,方向向量不同所构成的方向导数大小也不同,但是这些方向导数的方向始终会在一个平面内,这个平面就是这个点的切平面!
3、梯度:
梯度是方向导数的特例:
gradf(x,y)=∂x∂fi˙+∂y∂fj˙
已知在某个点有方向导数存在下列关系:
∂l∂f=∂x∂fcosφ+∂y∂fsinφ={∂x∂f,∂y∂f}⋅{cosφ,sinφ}
在方向l上满足如下单位向量:
e
=cosφi
+sinφj
则方向导数可转化成如下:
 点积就相当于做一个投影,方向导数 和 梯度 之间保持一定的夹角(做点积)来构成各个方向上的方向导数。什么时候方向向量最大呢?很容易想到不存在夹角的时候就可以满足,因为此时点积最大即满足下列条件:
点积就相当于做一个投影,方向导数 和 梯度 之间保持一定的夹角(做点积)来构成各个方向上的方向导数。什么时候方向向量最大呢?很容易想到不存在夹角的时候就可以满足,因为此时点积最大即满足下列条件:
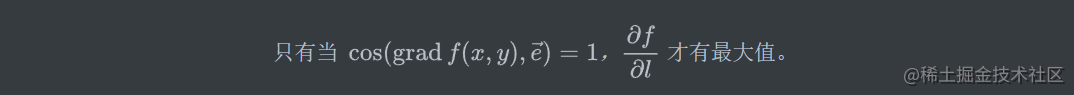
函数在某点的梯度是个向量,他的方向与方向导数最大值取值的方向一致,其大小正好是最大的方向导数。
梯度概念理解:如下图所示,在p点放一个热源的等温线,则热源的辐射从里到外为10°、20°、30°、40°,若一个小蚂蚁在o点,要最快逃离热源,应该往oj方向逃离,若往om方向逃离则热源的变化率为0,即一直都是20°,也就是说蚂蚁一旦确定了某个逃离方向(0°,90°)方向角逃离,只要一直沿着该方向一直走,就是最快的热源降低的方向
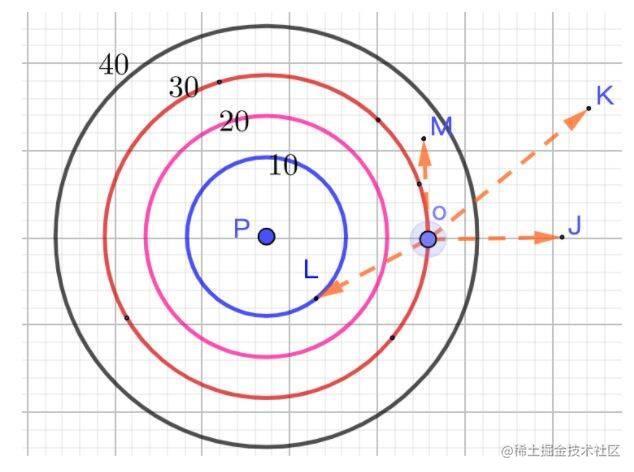
对于一维线性函数其导数就是梯度。
各种函数的梯度与导数的关系:
函数梯度
更详细的解释可以参考参考文献链接。
Tensor的梯度与反向传播
回顾机器学习
收集数据
x ,构建机器学习模型
f,得到
f(x,w)=Ypredict
如何判断模型的好坏?判断模型好坏的方法:
loss=(Ypredict−Ytrue )2loss=Ytrue ⋅log(Ypredict ) (回归损失) (分类损失)
通过最终
loss 的输出,来反向传播计算梯度大小进而调整参数的大小实现最优解。
当
loss 满足如图时候
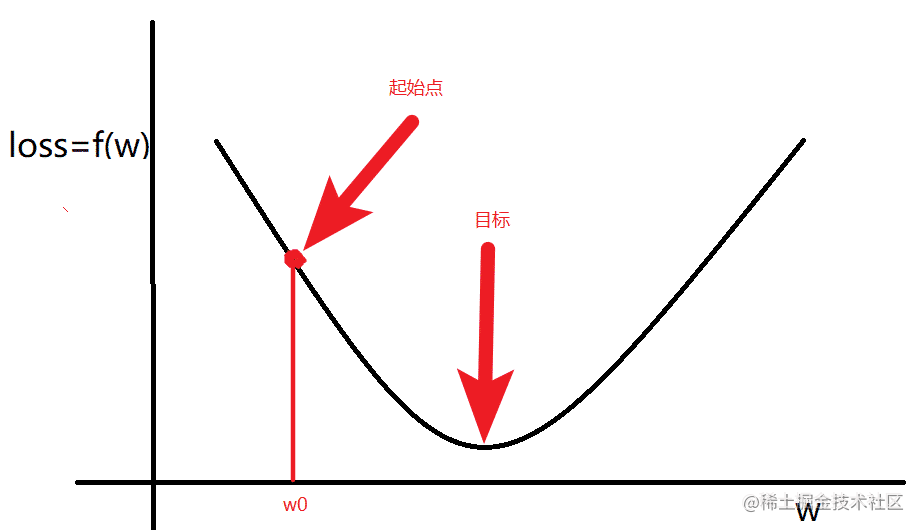
计算出来梯度以后:朝着梯度变化的方向运算,随机选择一个起始点
w0,通过调整
w0,让
loss 函数取到最小值。
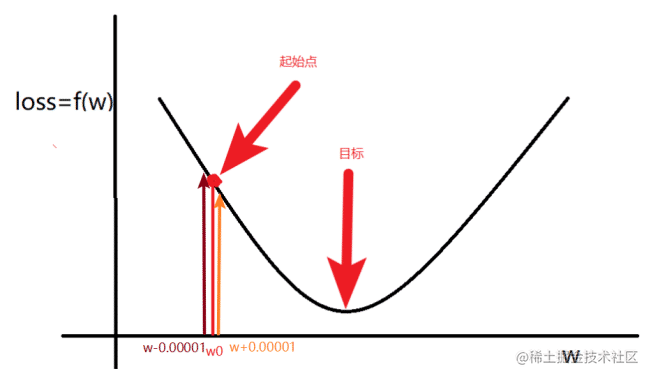
w的更新方法:
- 计算
w的梯度(导数)
\begin{align*} \nabla w = \frac{f(w+0.000001)-f(w-0.000001)}{2*0.000001} \end{align*}
- 更新
w
w=w−α∇w
其中:
-
∇w<0 ,意味着w将增大
-
∇w>0 ,意味着w将减小
总结:梯度就是多元函数参数的变化趋势(参数学习的方向),只有一个自变量时称为导数,拥有多个时称为偏导数。
反向传播?
计算图
为了方便描述,通过图的方式来描述函数。
J(a,b,c)=3(a+bc),令u=a+v,v=bc,把它绘制成计算图可以表示为:
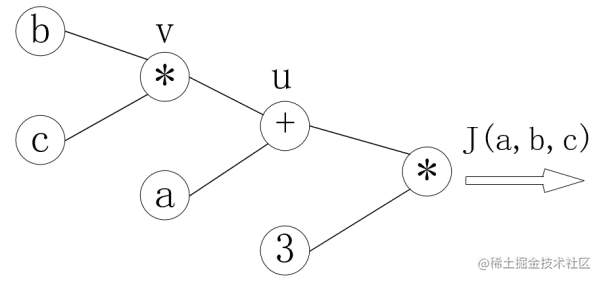
对每个节点求偏导可有:
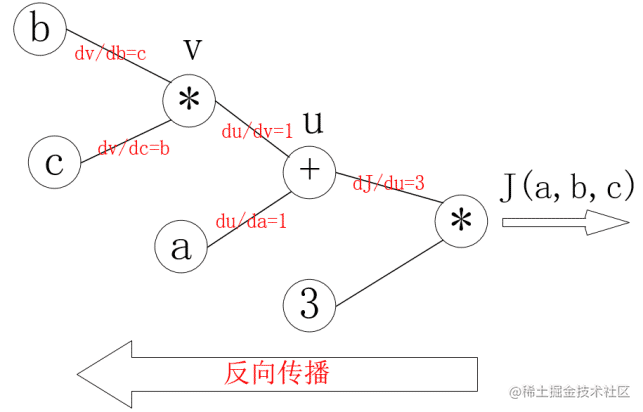
反向传播的过程就是一个上图的从右往左的过程,自变量
a,b,c各自的偏导就是连线上的梯度的乘积:
\begin{align*} \frac{dJ}{da} &= 3 \times 1 \\ \frac{dJ}{db} &= 3 \times 1 \times c \\ \frac{dJ}{dc} &= 3 \times 1 \times b \end{align*}
为什么要算反向传播?
因为要计算梯度。
实战演示:
接下来尝试计算一个简单结构的梯度,问题描述如下:
假设我们的基础模型就是y = wx+b,其中w和b均为参数,我们使用y = 3x+0.8来构造数据x、y,所以最后通过模型应该能够得出w和b应该分别接近3和0.8。
简单的来说就是拟合出满足y = 3x+0.8这个曲线。
步骤分为四步:
过程如下图:
从左向右是正向传播部分
从右向左是反向传播部分
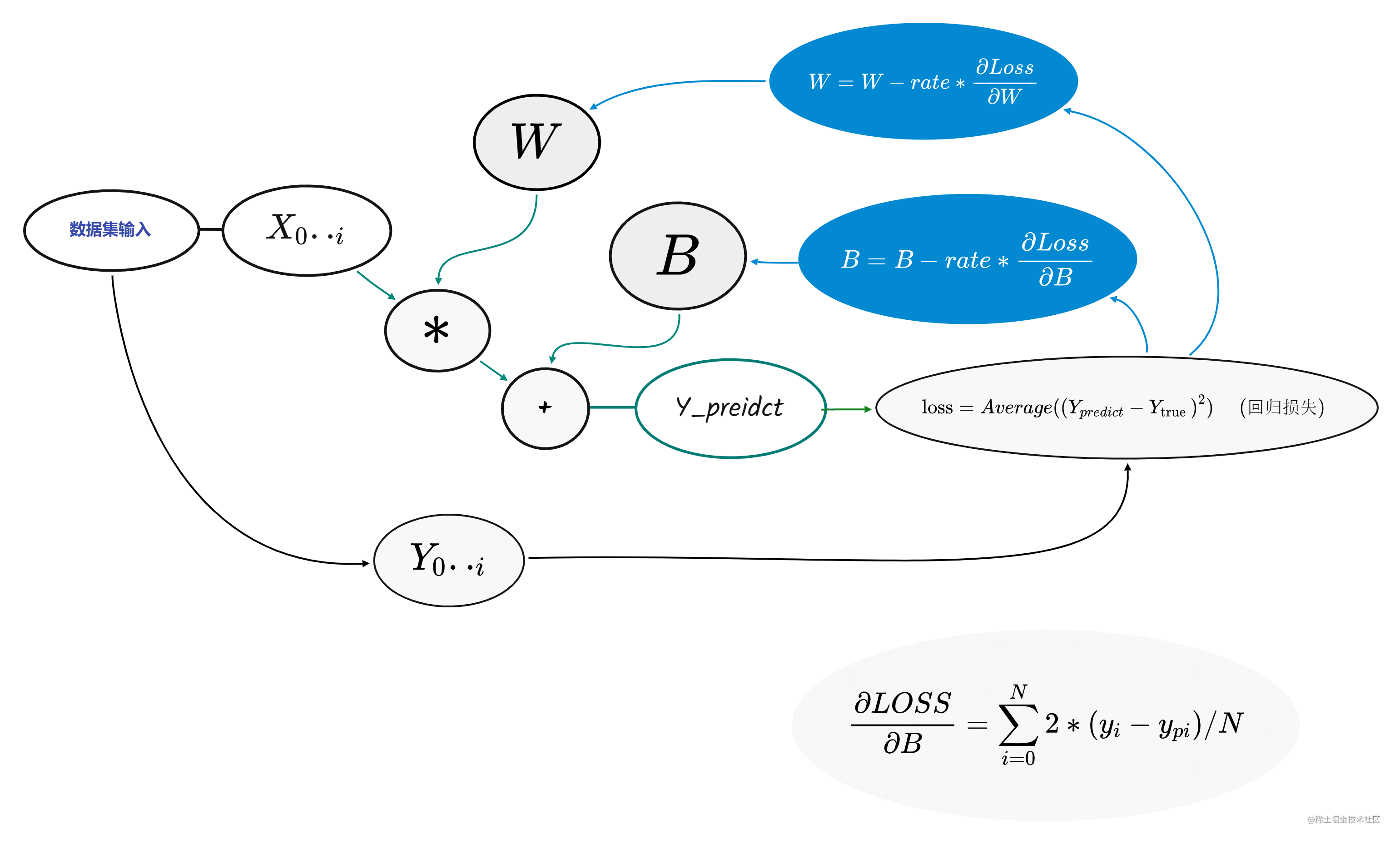
对于W和B其计算类似这里单独说B即可
对于B的梯度满足下式,值得注意的是这里的Loos求取的是平均值实际上出来的是一个标量,对于标量的梯度计算实际上也是一个平均值(这里值得思考一下)。
∂B∂Loss=i=0∑N2∗(yi−ypi)/N
反向传播后对B进行梯度下降:
B=B−rate∗∂B∂Loss
梯度下降以后再次进行正向传播即可,计算出来Y_p,最后计算出来Loss。
正向传播满足下式:
Ypredict(0...N)=Xpredict(0...N)∗W+B
代码如下:
import torch
import numpy as np
import matplotlib.pyplot as plt
x_number = 50
x = torch.rand([x_number, 1])
y = 3 * x + 0.8
rate = 0.01
study_time = 3000
w = torch.rand([1, 1], requires_grad=True, dtype=torch.float32)
b = torch.rand(1, requires_grad=True, dtype=torch.float32)
y_preidct = torch.matmul(x, w) + b
def forward_propagation():
global x, w, b, y_preidct
y_preidct = torch.matmul(x, w) + b
loss = (y - y_preidct).pow(2).mean()
return loss
def back_propagation():
global x, w, b, loss, rate, y_preidct
test = 0.0
if w.grad is not None:
w.grad.data.zero_()
if b.grad is not None:
b.grad.data.zero_()
loss.backward()
w.data -= w.grad * rate
b.data -= b.grad * rate
for i in range(study_time):
loss = forward_propagation()
back_propagation()
if i % 10 == 0:
print("w,b,loss", w.item(), b.item(), loss.item())
predict = x * w + b
plt.scatter(x.data, y.data, c="r")
plt.plot(x.data.numpy(), predict.data.numpy())
plt.show()
红色的是数据集结果蓝色是训练出来的结果:
当训练次数比较少的时候拟合曲线不正确:
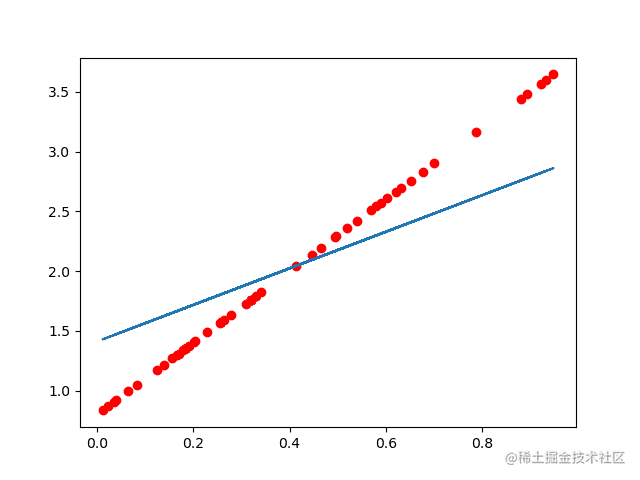
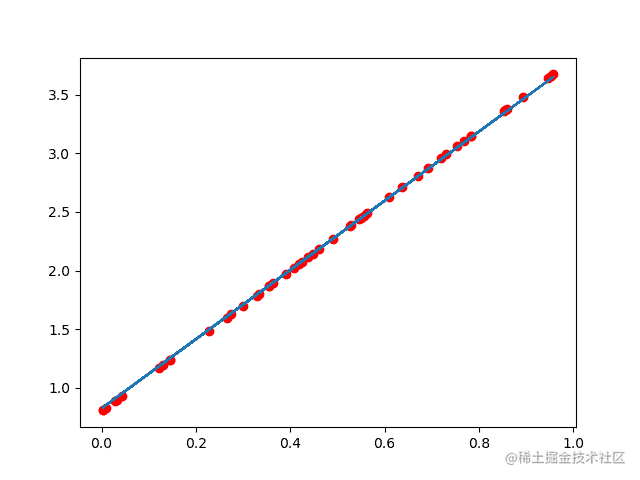
当把学习率降低(变化范围减小),增加学习次数就可以得到很好的结果:
参考文献:
国内教程 偏理论 (10 -13 节)
youtobe教程 (第三节)(需要科学上网)有需要搬运联系我
方向导数1
方向导数2
点积就相当于做一个投影,方向导数 和 梯度 之间保持一定的夹角(做点积)来构成各个方向上的方向导数。什么时候方向向量最大呢?很容易想到不存在夹角的时候就可以满足,因为此时点积最大即满足下列条件: