§00 命题说明

一、命题要求

1、命题题型

本次命题是面向2022年本科“信号与系统分析”课程的期末考试题。题目的类型、数量以及分值规划如下：

【表1-1 命题类型以及数量规划】

序列号	题目类型	题目数量	总分值	小分值	备注
1	选择题	10	10	1	考察基本概念
2	判断对错题	5	5	1	变形的选择题
3	填空题	6	15	2	简化的计算题
4	简答题	3	15	5	对于课堂内容的讨论与延伸考察基本概念、分析以及应用的能力判罚标准比较灵活。
5	计算题	5	25	5	变形的作业题
6	综合题	3	30	10	综合分析能力；题目不难，大部分分之是作业送分题

2、命题内容覆盖分析

【表1-2 各章内容覆盖】

章节	题目	总分值
第一章	1-1(1),1-2(1),2-2(1),2-3(1)	4
第二章	5-5(5),8(10)	15
第三章	1-6(1).1-9(1),2-1(1),5-1(5)	8
第四章	1-5(1),7(12)	13
第五章	1-8(1),3-2(2),3-5(3),5-2(5),5-3(5)	16
第六章	1-4(1),1-10(1),2-4(1),2-5(1),3-3(3),3-4(3),3-6(2),5-5(5),6(8)	25
第七章	4-3(5),3-1(2),4-3(5),5-4(5)	17
第八章	1-3(1),1-7(1),2-2(1),4-1(5),4-2(5)	13

A\B试卷调整说明：

最初试卷是A卷，按照以下方式将其调整到B卷。

大题调整：
- A卷中的大题顺序为：1,2,3,4,5,6,7,8
- B卷中的答题顺序为：2,3,4,3,6,5,8,7
小题调整：
- 对应A卷中的 1,2,3,4,5中都分别有小题；将小题按照奇数偶数对调；

3、考试相关内容

（1）考试时间地点

▲ 图1.1 考试时间与地点

▲ 图1.1 考试时间与地点

（2）成绩录入

2022年6月2日（星期四）8:30 - 2022年7月8日（星期五）17:00
2022届本科毕业生成绩录入截止时间：2022年6月19日（星期日）24:00

4、网络考试须知

2022信号与系统课程网络考试须知

1. 考试的时间节点：考试日期：2020年6月13日上午：9:00 - 11:00（11:30）
（1）每位同学登录指定的腾讯会议的时间 8:40
将自己的摄像头打开，指向自己的正面；需要将自己的腾讯麦克打开，让助教能够听到你的周围环境声音。
（2）进入会议时，将自己的显示名称修改为：
姓名+学号+班级
（3）下载试题的时间：8:50分
（4）答题时间：9:00 至 11:00
（5）拍照上传答案时间：11:00 至12:00分

注意：最终结束时间会根据同学们考试进程，或者网络考试中出现的状况进行适当调整，届时会有监考助教在腾讯会议提前提醒大家。

2. 监考要求
（1）每个同学需要独立完成考试，不允许通过网络与其他同学进行信息交换；
（2）考试过程不允许参考教材，作业以及其他辅导材料。可以参考自己总结的A4纸上的内容。
（3）考试过程需要保持自己的摄像头始终打开，如果出现网络问题，需要及时通过腾讯会议“聊天”，或者在班级群里向监考老师说明情况。
（4）在考试过程中如果有疑问可以向监考助教及时提出。

3. 收卷要求
（1）所有的答案都需要通过自己手工书写完成；并最终将拍照后的图片合并成PDF文件，或者嵌入WORD文档上传。文件内容包括：含有答案的试卷（选择题、判断对错题、填空题）、答题纸、A4复习纸。
手写方式可以采用以下方式之一：
A. 下载打印试卷，将选择题、判断对错题、填空题填写在试卷上，其余各题按照顺序写在自己的答题纸上；
B.将所有的答案都按照顺序写在自己的答题纸上；
（3）在提交的答案第一页，必须包括以下信息：
A. 誊写有“网络考试诚信承诺书”，并有自己的签名；
B. 学生证的正面；
C. 自己的姓名、学号、班级。

4. 其他注意事项：
（1）在考试中，请大家注意试卷的题目数量，不要遗漏的试题。
（2）在答题纸上需要将试题的序号填写清楚。
（3）遇到问题请及时与监考的助教和任课教师通过网络进行沟通。

任课教师的手机：13501115467
监考助教的手机他们将会在各自会议室告诉大家。
最后祝大家考试顺利。考试完之后请尽快准备课程的小论文，请注意小论文的最终截止日期。

§01 考试命题

一、选择题

题目要求：单项选择题：（10×1=10分，将答案写在试卷前面的答案表格1中）

1、下面信号中，哪一个是能量有限信号？
$A.\,\,\,\,e^{ - 3t} \cdot u\left( t \right);\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,B.\,\,\,\,\,\delta \left( t \right);$ $C.\,\,\,\,u\left( {2t} \right);\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,D.\,\,\,\,\sin \left( {\omega _0 t} \right)$

解答： A
信号的能量定义为 $\int_{ - \infty }^{ + \infty } {\left| {f\left( t \right)} \right|^2 dt}$ 。根据这个定义，可以知道：
$E_A = \int_0^\infty {\left| {e^{ - 3t} } \right|^2 dt} = \int_0^\infty {e^{ - 6t} dt} = {1 \over { - 6}} \cdot \left. {e^{ - 6t} } \right|_0^{ + \infty } = {1 \over 6}$ $E_B = \int_{ - \infty }^{ + \infty } {\left| {\delta \left( t \right)} \right|^2 dt} = \infty$ $E_C = \int_0^{ + \infty } {u^2 \left( {2t} \right)dt} = + \infty$ $E_D = \int_{ - \infty }^{ + \infty } {\sin ^2 \left( {\omega _0 t} \right)dt} = \int_{ - \infty }^{ + \infty } {\left( { { {1 - \cos 2\omega _0 t} \over 2}} \right)dt} = \infty$

2、下面信号，哪一个是周期信号 ？
$A.\,\,\,\,x\left[ n \right] = \cos \left[ { { {2\pi n^2 } \over 3}} \right];\,\,\,\,\,\,\,\,\,\,\,\,B.\,\,\,\,x\left( t \right) = e^{ - j3.14t} + e^{ - j2\pi t} ;$ $C.\,\,\,\,x\left( t \right) = \cos 2t + \sin \pi t;\,\,\,\,\,\,\,\,D.\,\,\,\,x\left[ n \right]\,\,\, = \sin ^2 \left[ {2n} \right];$

解答： A
A 序列的周期为3。 $x\left[ {n + 3} \right] = \cos \left[ { { {2\pi } \over 3}\left( {n + 3} \right)^2 } \right] = \cos \left[ { { {2\pi } \over 3}\left( {n^2 + 6n + 9} \right)} \right] = \cos \left[ { { {2\pi } \over 3}n^2 } \right]$
B，C 都是两个连续周期信号的叠加，但两个周期信号的频率（或者周期）比值为无理数，所以它们不是周期信号；
D 序列信号的归一化频率和 2 $\pi$ 的比值不是有理数，所以它是非周期信号；
注：对于周期序列信号，可以看一个连续周期信号与采样周期序列的成绩，所以要求归一化频率与 $2\pi$ 的比值为有理数时，才是真正的周期信号。

3、已知长度 $N = 8$ 的FIR滤波器是线性相位，它的前四个滤波器系数为1,2,3,4，请问下面哪一组数字是该滤波器的后四个滤波器系数？

$A.\,\,\,\,\,\,1,4,3,2;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,B.\,\,\,\,\,\,1,2,3,4;$ $C.\,\,\,\,\,\,4,3,2,1;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,D.\,\,\,\,\,\,1,3,2,4;$

解答： C
对于FIR滤波器，它的滤波器系数关于长度中心参数 $\left( {N - 1} \right)/2$ 呈现偶对称，或者奇对称，对应的滤波器的相位特性为线性相位。在给定的四个答案中，C对应的四个数字与前面四个滤波器系数呈现偶对称。

4、下面各图中LTI系统函数的零极点分布，所描述的幅频特性为带阻系统为：（）

解答： C
（A）：低通特性；（B）带通特性；（C）带阻特性；（D）全通特性；

5、信号为等幅正弦波，它的单边带调制信号波形为：（）

解答： A
A：单边带调幅；B：普通调幅信号；C：调幅信号平方；D：载波抑制调幅信号；
这个题目在期中随堂练习出现过。

6、如果对二维图像进行傅里叶变换，图像的边缘信息蕴含在图像频谱的哪一部分？

A. 幅度谱； B. 相位谱;
C. 频谱的实部； D. 频谱的虚部；

解答： B
参考 信号与系统2022春季学期第六次作业 中的 实验题目：信号频谱内的信息 。

7、如果使用匹配滤波器来检测接收信号中的时间延迟，那么下面四个信号中哪一个最适合作为发送信号？

解答： D
根据匹配滤波器的特点，要求发送的信号的自相关能量约集中越好，使得时间延迟检测更加准确。
下面是四个信号的波形。

▲ 四个信号波形
下面上面四个信号的自相关波形。
▲ 四个信号自相关的波形

from headm import *

A = [1]*1000
B = [1]*500 + [-1]*500
C = cos(linspace(-pi,pi,1000, endpoint=True))*0.5+0.5
D = cos(linspace(0, 5*pi,1000,endpoint=True)**2)

A = convolve(A,A[::-1])
B = convolve(B,B[::-1])
C = convolve(C,C[::-1])
D = convolve(D,D[::-1])

dim = [A,B,C,D]
label = ['A*A[::-1]','B*B[::-1]','C*C[::-1]','D*D[::-1]']

for i in range(4):
    plt.subplot(220+(1+i))
    plt.plot(dim[i], label=label[i])

    plt.xlabel("n")
    plt.ylabel("ABCD")
    plt.title(label[i])
    plt.grid(True)
    plt.tight_layout()

plt.show()

8、可能与下面s平面区域对应的z平面区域为（）：

解答： D
具体内容可以参见 2022年信号与系统春季第十一次作业中的实验作业内容 。

9、已知信号的幅度谱和相位谱如下图所示：

将该信号反褶之后，再往左平移时间 a ,信号的相位谱为：

解答： D
求解可以参见 信号与系统2022年第六次作业中1.3.1信号相位变化对信号影响 。

10、 已知离散时间LTI系统的系统函数 $H\left( z \right)$ 的零极点分布如下图所示，其中幅频特性为全通系统的是：

求解： C
对于离散时间系统中的全通系统，要求其系统函数的零极点成对出现，并呈现倒共轭对称。即零点等于极点的倒数取共轭。

二、判断对错

题目要求：判断对错题：（5×1=5分，正确画√，错误画×，结果写在试卷前面的答案表格2中）

1、恒等式 $\sum\limits_{n = - \infty }^{ + \infty } {e^{ - j\omega n} } = 2\pi \sum\limits_{n = - \infty }^{ + \infty } {\delta \left( {\omega - 2\pi n} \right)}$ 是正确的。

解答： 正确。
因为： $F\left\{ {\sum\limits_{n = - \infty }^{ + \infty } {e^{ - jnt} } } \right\} = 2\pi \sum\limits_{n = - \infty }^{ + \infty } {\delta \left( {\omega - n} \right)}$ $F\left\{ {2\pi \sum\limits_{n = - \infty }^{ + \infty } {\delta \left( {t - 2\pi n} \right)} } \right\} = 2\pi \sum\limits_{n = - \infty }^{ + \infty } {\delta \left( {\omega - n} \right)}$ 所以 $\sum\limits_{n = - \infty }^{ + \infty } {e^{ - jnt} } = 2\pi \sum\limits_{n = - \infty }^{ + \infty } {\delta \left( {t - 2\pi n} \right)}$ 所以原式也成立，即将 $t$ 替换成 $\omega$ 即可。
注：本题是郑君里：信号与系统教材上册，第二章课后习题。

2、微分系统的系统函数不满足佩里-维纳准则，但它是因果系统。

解答： 正确。
微分系统 $y\left( t \right) = dx\left( t \right)/dt$ 的传递函数 $H\left( {j\omega } \right) = j\omega$ 。它不满足佩利（Paley）-维纳（Weiner）准则中关于系统函数绝对可积的要求。但是微分运算，在国内信号与系统教科书中是作为因果运算来看待的。

3、一个周期信号与一个非周期信号叠加的结果有可能是周期信号。

解答： 正确。
通常情况下，周期信号与非周期信号的叠加是非周期信号。
下面给出周期信号与非周期信号叠加产生周期信号的情况。两个周期信号 $f\left( t \right),g\left( t \right)$ 叠加 $h\left( t \right) = f\left( t \right) + g\left( t \right)$ 有可能是非周期信号，即当 $f\left( t \right),g\left( t \right)$ 的周期比值为无理数的时候， $h\left( t \right)$ 为非周期信号。因此， $f\left( t \right) + \left[ { - h\left( t \right)} \right]$ 是周期信号与非周期信号的叠加，而对应的 $g\left( t \right)$ 是周期信号。

4、如果一个线性时不变离散时间系统的系统函数的收敛域包含单位圆，则系统是BIBO稳定的。

解答： 正确。
如果 $H\left( z \right)$ 的收敛域包含单位圆，说明 $H\left( {e^{j\omega } } \right)$ 存在，也意味着 $\sum\limits_{n = - \infty }^{ + \infty } {\left| {h\left( n \right)} \right|} < \infty$ 。系统单位冲激响应绝对可和是系统BIBO稳定的充要条件。

5、任何一个线性时不变系统都可以分解成一个最小相位系统与全通系统的级联。

解答： 正确。
以连续时间系统为例，如果它的系统函数中，包含有位于虚轴右边的零点，那么可以将其零点以虚轴为对称平移到虚轴左边，与原有的零极点构成最小相位系统，然后在令这些零点与其在虚轴左边对称的极点形成全通系统。它们级联后，便可以获得与原来系统相同的系统函数。这个过程可以看成对任意有理分式确定的线性时不变系统进行最小相位系统与全通系统分解的过程。

三、填空题

题目要求：填空题：（2+2+3+3+3+2=15分，将答案写在题目中空线上）

1、已知序列 $x\left[ n \right]$ 长度 $N = 4$ ，如下图所示：

$y\left[ n \right] = x\left[ n \right] \otimes _5 x\left[ n \right]$

则： $y\left[ 2 \right] =$ 3 。

其中 $\otimes _5$ 是长度为 5 的圆卷积。

解答： $y\left[ 2 \right] = 3$ 。
$x\left[ n \right] = \left\{ {0.5,2, - 1,1,0} \right\}$ ， $x\left[ n \right] \otimes _5 x\left[ n \right] = \left\{ { - 1.75,3,3, - 3,5} \right\}$

a = array([0.5,2,-1,1,0])
b = real(fft.ifft(fft.fft(a)**2))
printf(b)

2、已知信号的拉普拉斯变换为：
$X\left( s \right) = { {2s^2 + s + 1} \over {s\left( {s + 2} \right)}},\,\,{\mathop{\rm Re}\nolimits} \left( s \right) > 0$

则信号的初值 $x\left( {0_{ + } } \right) =$ -3 ；信号的中值 $x\left( { + \infty } \right) =$ 0.5 。

利用拉普拉斯初值定理求解信号的初值时，需要把拉普拉斯变换表达式通过长除法分解成 s 多项式加上一个 s 的真有理分式。 $X\left( s \right) = { {2s^2 + s + 1} \over {s\left( {s + 2} \right)}} = 2 + { { - 3s + 1} \over {s^2 + 2s}} = 2 + X_1 \left( s \right)$ 此时对应的初值往前走 $x\left( {0_ + } \right) = \mathop {\lim }\limits_{s \to \infty } sX_1 \left( s \right) = \mathop {\lim }\limits_{s \to \infty } { { - 3s + 1} \over {s + 2}} = - 3$ 利用拉普拉斯终值定理可以计算出 $x\left( \infty \right) = \mathop {\lim }\limits_{s \to 0} s \cdot X\left( s \right) = \mathop {\lim }\limits_{s \to 0} s \cdot { {2s^2 + s + 1} \over {s\left( {s + 2} \right)}} = 0.5$
求解 $X\left( s \right)$ 的拉普拉斯反变换，可得： $x\left( t \right) = 2\delta \left( t \right) + {1 \over 2} - {7 \over 2}e^{ - 2t} ,\,\,\,t \ge 0$

3、下面系统中为了保证系统是稳定的，参数K的取值范围是： $K > 2$ 。

求解过程参见课件： 6.2.2.1
$H\left( s \right) = {1 \over {s^2 + s + 2 + K}}$ 根据Routh判据，可以知道相应的结果。

4、一个线性时不变系统的输入输出分别是 $x\left( t \right),y\left( t \right)$ ，它们之间的关系可以由下面的微分方程所描述：
$\over {dt}}w\left( t \right) = y\left( t \right) + x\left( t \right)$ $\over {dt}}y\left( t \right) = - w\left( t \right)$

其中 $w\left( t \right)$ 是中间变量。

那么该系统的系统函数为：
$H\left( s \right) = { {Y\left( s \right)} \over {X\left( s \right)}} = - {1 \over {s^2 + 1}}$
系统的单位冲激响应 $h\left( t \right) = - \sin \left( t \right) \cdot u\left( t \right)$ 。

5、已知序列 $x\left[ n \right]$ 对应的Z变换为 $X\left( z \right)$ ，那么它的补零三倍拉伸序列信号 $x_1 \left[ n \right] = x\left[ {n/3} \right]$ 对应的Z变换为: $X\left( {z^3 } \right)$ 。

6、已知连续时间 LTI 系统的单位冲激响应信号波形如下图(A) ~ (F)所示，在下图后面给出了六种零极点分布示意图(1) ~ (6)，请按照(A) ~ (F)对应单位冲激响应波形写出对应系统零极点分布顺序: （4），（5），（6），（1），（2），（3）。

四、简答题

1、匹配滤波器

请简要说明匹配滤波器的特点以及应用的条件。

◎ 解答：

关于匹配滤波器的特点，能够包含以下一个或者多个内容即可：

（1） 匹配滤波器的单位冲激响应 $h\left( t \right)$ 是待检测信号 $s\left( t \right)$ 反褶经过延迟之后形成的信号，即 $h\left( t \right) = k \cdot s\left( {t_m - t} \right)$ ，其中 $k,t_m$ 是常量；

（2） 匹配滤波器实际上是将待检测信号 $s\left( t \right)$ 与接收到的信号 $\cdot s\left( {t - t_m } \right) + n_0 \left( t \right)$ 做相关运算，通过检测相关结果的峰值确定信号延迟以及相应的幅值。

关于匹配滤波器应用条件，需要包括以下两点：

（1） 已知待检测信号的波形 $s\left( t \right)$ ，检测接受信号中待检测信号的延迟和幅值；

（2） 接受信号中包括待检测信号的无失真延迟和白色噪声，即 $\cdot s\left( {t - t_m } \right) + n_0 \left( t \right)$ 。

2、因果系统条件

如果已知连续时间系统的系统函数 $H\left( \omega \right) = R\left( \omega \right) + jX\left( \omega \right)$ ，请列举两个判断其为因果系统的必要条件。

◎ 解答：

第一个必要条件：佩里（Paley）-维纳（Wiener）准则，是从滤波器的幅频特性判因果性的必要条件。包括两个不等式： $\int_{ - \infty }^{ + \infty } {\left| {H\left( \omega \right)} \right|^2 d\omega } < \infty$ $\int_{ - \infty }^{ + \infty } { { {\left| {\ln \left| {H\left( \omega \right)} \right|} \right|} \over {1 + \omega ^2 }}d\omega } < \infty$
第二个必要条件：系统函数（傅里叶变换下定义的系统函数）的实部和虚部之间满足希尔伯特变换，即 $R\left( \omega \right) = X\left( \omega \right) * {1 \over {\pi \omega }} = {1 \over \pi }\int_{ - \infty }^{ + \infty } { { {X\left( \lambda \right)} \over {\omega - \lambda }}d\lambda }$ $X\left( \omega \right) = - R\left( \omega \right) * {1 \over {\pi \omega }} = - {1 \over \pi }\int_{ - \infty }^{ + \infty } { { {R\left( \lambda \right)} \over {\omega - \lambda }}d\lambda }$

3、频率泄露

什么是“频率泄露”现象？如何减少频谱泄露对于频谱分析的影响？

◎ 求解：

在回答的内容中包括有以下内容中的要点：

（1） 频率泄露现象是在使用离散傅里叶变换（DFT）分析连续时间信号频谱中，将频域信号截断成有限长信号时引起频谱发生的变化；

（2） 频谱变化包括有：在频谱的幅值出现波动；在频谱幅值突变范围内出现过渡带；

（3） 减少频谱泄露现象可以采用两种措施：第一种措施是增加对时域信号截取时间长度，可以减少频谱中出现的过渡带的范围；第二种措施是选择较为光滑的窗口函数截取时域信号，可以减少频谱波动的幅度，第二种方法也会同时加大频谱过渡带的宽度。

五、计算题

1、傅里叶反变换

已知信号 $f\left( t \right)$ 的频谱 $F\left( \omega \right) = {\mathop{\rm Re}\nolimits} \left[ {e^{ - j2\omega } \cdot {1 \over {j\omega + 3}} + \delta \left( \omega \right)} \right]$

求 $f\left( t \right)$ 的表达式。

◎ 求解： 假设 $g\left( t \right)$ 的频谱为 $G\left( \omega \right) = e^{ - j2\omega } \cdot {1 \over {j\omega + 3}} + \delta \left( \omega \right)$ 那么 $f\left( t \right)$ 是 $g\left( t \right)$ 的偶分量，即 $f\left( t \right) = {1 \over 2}\left[ {g\left( t \right) + g\left( { - t} \right)} \right]$

下面先求 $g\left( t \right)$ 的表达式。

由

那么

再由

由傅里叶变换的线性性，可以知道

$g\left( t \right) = {1 \over {2\pi }} + e^{ - 3\left( {t - 2} \right)} \cdot u\left( {t - 2} \right)$ 所以 $f\left( t \right) = {1 \over 2}\left[ {g\left( t \right) + g\left( { - t} \right)} \right] = {1 \over {2\pi }} + {1 \over 2}\left[ {e^{ - 3\left( {t - 2} \right)} u\left( {t - 2} \right) + e^{3\left( {t + 2} \right)} u\left( { - t - 2} \right)} \right]$

2、拉普拉斯变换

已知单边周期信号 $f\left( t \right)$ 的波形如下，求 $f\left( t \right)$ 的拉普拉斯变换。

◎ 求解：

假设 $f_0 \left( t \right)$ 是 $f\left( t \right)$ 在 $\left[ {0,2} \right]$ 之间的单个周期信号。下面先求 $f_0 \left( t \right)$ 的拉普拉斯变换。

利用拉普拉斯的微分和积分性质求解 $f_0 \left( t \right)$ 的拉普拉斯变换。将 $f_0 \left( t \right)$ 进行两次微分，可以得 $f''_0 \left( t \right)$ ，波形如下：

对于 $f''_0 \left( t \right)$ ，对应的拉普拉斯变换为： $L\left[ {f''_0 \left( t \right)} \right] = s - e^{ - s} + e^{ - 2s}$

在根据拉普拉斯变换延时性质，可得 $L\left[ {f\left( t \right)} \right] = {1 \over {1 - e^{ - 2s} }}L\left[ {f_0 \left( t \right)} \right] = { {s - e^{ - s} + e^{ - 2s} } \over {s^2 \left( {1 - e^{ - 2s} } \right)}}$

为了验证上面结果，使用 信号与系统2022春季作业-第十次作业 中实验作业中的Laplace数值反变换，可以计算上面结果对应的时域信号，如下：
▲ 数值对结果进行反变换

#------------------------------------------------------------
def invlt(t, fs, sigma, omiga, nint):
    omigadim = linspace(0, omiga, nint+1, endpoint=True)
    y = [(exp(1j*o*t) * fs(sigma+1j*o)).real for o in omigadim]
    y_left = y[:-1]
    y_right = y[0:]
    T = sum(y_right + y_left) * omiga/nint
    return exp(sigma*t) * T/ pi / 2

#------------------------------------------------------------
def fs(s):
#    return 1/(s*s+1)
    return (s-exp(-s)+exp(-2*s))/(s**2*(1-exp(-2*s)))

#------------------------------------------------------------
sigma = 0.2
omiga=200
nint=omiga*50

tdim = linspace(0, 5, 500)
ft = [invlt(t, fs, sigma, omiga, nint) for t in tdim]

#------------------------------------------------------------

plt.plot(tdim, ft)

plt.xlabel("t")
plt.ylabel("f(t)")
plt.grid(True)
plt.tight_layout()
plt.show()

3、z反变换

已知某一变换的象函数
$X\left( z \right) = { {z^2 } \over {\left( {z - 0.5} \right)\left( {z - 2} \right)}}$
收敛域为 $\left| z \right| < 2$ ，求出原序列。

◎ 求解： 利用部分分式展开法：

$X\left( z \right) = - {2 \over 3}{z \over {z - 0.5}} + 2{2 \over 3}{z \over {z - 2}}$

当 $\left| z \right| < 1$ ，原序列是双边序列。其中 $X\left( z \right)$ 第一项对应是一个右边序列，第二项对应是一个左边序列：

$x\left[ n \right] = - {2 \over 3}\left( { {1 \over 2}} \right)^n \cdot u\left[ n \right] - 2{2 \over 3} \cdot 2^n \cdot u\left[ { - n - 1} \right]$

4、离散傅里叶变换

已知长度为 $N$ 的序列
$x\left[ n \right] = \sin { {n\pi } \over N},\,\,n = 0,1,2, \cdots ,N - 1$

求该序列的离散傅里叶变换（DFT）。

注：要求将结果化简到没有累加和的实数表达式。

◎ 求解： 根据离散傅里叶变换的公式，可知
$X\left[ k \right] = DFT\left\{ {x\left[ n \right]} \right\} = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right]e^{ - j{ {2\pi } \over N}nk} }$ $\sum\limits_{n = 0}^{N - 1} {\sin { {n\pi } \over N} \cdot e^{ - j{ {2\pi } \over N}nk} = \sum\limits_{n = 0}^{N - 1} { {1 \over {2j}}\left( {e^{j{\pi \over N}n} - e^{ - j{\pi \over N}n} } \right) \cdot e^{ - j{ {2\pi } \over N}nk} } }$ $\over {2j}}\sum\limits_{n = 0}^{N - 1} {e^{j{\pi \over N}\left( {1 - 2k} \right)n} } - {1 \over {2j}}\sum\limits_{n = 0}^{N - 1} {e^{ - j{\pi \over N}\left( {1 + 2k} \right)n} }$ $\over {2j}}\left[ { { {1 - e^{j\left( {1 - 2k} \right)\pi } } \over {1 - e^{j{ {1 - 2k} \over N}\pi } }} - { {1 - e^{ - j\left( {1 + 2k} \right)\pi } } \over {1 - e^{ - j{ {1 + 2k} \over N}\pi } }}} \right]$ $\over j}\left[ { { {e^{j{ {1 - 2k} \over N}\pi } - e^{ - j{ {1 + 2k} \over N}\pi } } \over {\left( {1 - e^{j{ {1 - 2k} \over N}\pi } } \right)\left( {1 - e^{ - j{ {1 + 2k} \over N}\pi } } \right)}}} \right]$ $\over j}\left[ { { {e^{ - j{ {2k} \over N}\pi } \left( {e^{j{\pi \over N}} - e^{ - j{\pi \over N}} } \right)} \over {e^{ - j{ {2k} \over N}\pi } \left( {e^{j{ {2k} \over N}\pi } - e^{j{\pi \over N}} } \right)\left( {1 - e^{ - j{ {1 + 2k} \over N}\pi } } \right)}}} \right]$ ${2\sin {\pi \over N}} \over {e^{j{ {2k} \over N}\pi } - e^{j{\pi \over N}} - e^{ - j{\pi \over N}} + e^{ - j{ {2k} \over N}\pi } }} = { {\sin {\pi \over N}} \over {\cos { {2k\pi } \over N} - \cos {\pi \over N}}}$

本题来自于两个渠道。（1） 2022年春季学期第十三次作业 2-1-5，将其中的 $\omega _0 = \pi /N$ ，这样便于将最终的结果进行化简。求解参见 求DFT的解答（5） 。（2）最终的求解结果参见 Fourier Analysis, Additional Exercises 中的第 64 道（最后一道）题目。
本题中考核对DFT定义，题目的难点在于对表达式的化简。需要利用欧拉公式把 $\sin \left( t \right)$ 转换成指数形式，然后比较有利于后面的化简。

5、求系统函数

已知LTI的系统框图如下图所示，请写出该系统的在拉普拉斯变换下的系统函数：

图中 $a, b$ 为常数。

◎ 求解：

先求求解系统对应的微分方程。假设系统中第一个积分输出的变量为 $w\left( t \right)$ ，那么可以写出系统框图中其它节点对应的变量。

根据两个综合器可以得到：

$x\left( t \right) - by'\left( t \right) = w'\left( t \right)$ $w\left( t \right) - ay\left( t \right) = y'\left( t \right)$

利用微分算则化简上述方程，最后可得输入输出之间的微分方程 $y''\left( t \right) + \left( {a + b} \right)y'\left( t \right) = x\left( t \right)$

利用拉普拉斯变换微分性质，对上述微分方程左右同时进行拉普拉斯变换，可得系统函数 $H\left( s \right) = { {Y\left( s \right)} \over {X\left( s \right)}} = {1 \over {s^2 + \left( {a + b} \right)s}}$

六、系统分析

题目要求：系统分析：（10分，将答案写在答题纸上，注明题目标号）

已知离散时间线性时不变系统的频率特性为： $H\left( {e^{j\Omega } } \right) = j\tan \left( \Omega \right)$

请：
（1） 写出该离散时间统对应的差分方程。

（2） 绘制出系统函数零极点分布，并判断系统幅频特性的特点，即属于低通，高通，带通，带阻哪一类滤波器。

提示： $j\tan \left( \Omega \right) = { {2j\sin \left( \Omega \right)} \over {2\cos \left( \Omega \right)}} = { {e^{j\Omega } - e^{ - j\Omega } } \over {e^{j\Omega } + e^{ - j\Omega } }}$

◎ 解答：

（1） 将系统的频率特性 $H\left( {e^{j\Omega } } \right)$ 的表达式写成关于 $e^{j\Omega }$ 的形式，便可以得到对应的系统方程。

根据 $2\cos \Omega = e^{j\Omega } + e^{ - j\Omega } ,2j\sin \Omega = e^{j\Omega } - e^{ - j\Omega }$ ，所以 $H\left( {e^{j\Omega } } \right) = j\tan \left( \Omega \right) = { {2j\sin \Omega } \over {\cos \Omega }} = { {e^{j\Omega } - e^{ - j\Omega } } \over {e^{j\Omega } + e^{j\Omega } }}$

将 $e^{j\Omega }$ 替换成 $z$ ，便可以得到系统的系统函数： $H\left( z \right) = { {z - z^{ - 1} } \over {z + z^{ - 1} }} = { {1 - z^{ - 2} } \over {1 + z^{ - 2} }} = { {Y\left( z \right)} \over {X\left( z \right)}}$ 于是 $Y\left( z \right)\left( {1 + z^{ - 2} } \right) = X\left( z \right)\left( {1 - z^{ - 2} } \right)$ 对应的差分方程为 $y\left[ n \right] + y\left[ {n - 2} \right] = x\left[ n \right] - x\left[ {n - 2} \right]$

（2） 系统的零极点分布如下：

该系统的幅频特性属于带通特性。

七、信号处理频谱分析

题目要求：信号处理频谱分析：（10分，将答案写在答题纸上，注明题目标号）

在下面的信号调制电路中， $\omega _c > > \omega _m$ 。低通滤波器（LPF）是理想低通滤波器，截止频率为 $\omega _m /2$ 。

▲ 图1.6.1 信号调制与解调框图

已知输入信号 $x\left( t \right)$ 的频谱 $X\left( {j\omega } \right)$ 如下图所示。请绘制出上图中 ① ～ ⑥ 处的信号以及输出信号 $y\left( t \right)$ 的频谱，在绘制频谱图中标明重要的频率与幅值对应的数值。

注：如果某一处的频谱 $G\left( {j\omega } \right)$ 为纯虚数，则绘制 $\cdot G\left( {j\omega } \right)$ 对应的实数频谱。

▲ 图1.6.2 输入信号的的频谱X(jomiga)

◎ 求解：

（1） ~ （3）点的频谱如下面三个小图所示：

▲ 图1.6.3 （1）点处的频谱

▲ 图1.6.4 （2）点处的频谱

▲ 图1.6.5 （3）点处的频谱

由于（4），（5）两处的频谱为纯虚频谱，下面绘制出对应的 $jX_4 \left( {j\omega } \right), - jX_5 \left( {j\omega } \right)$ 对应的频谱图。

▲ 图1.6.6 （4）点处的频谱

▲ 图1.6.7 （5）点处的频谱

下面是（6）处的频谱图。

▲ 图1.6.8 （5）点处的频谱

将（3），（6）两处的频谱叠加之后，形成的频谱如下图所示：

八、卷积运算

已知LTI系统的单位冲激响应为 $h\left( t \right) = e^{ - t} \left[ {u\left( t \right) - u\left( {t - 1} \right)} \right]$ 。系统的输入信号 $x\left( t \right)$ 如下图所示。求系统的零状态响应的 $y\left( t \right)$ 。

▲ 图1.6.10
注：利用卷积求解过程中，要求将信号 $h\left( t \right)$ 进行反褶。

这个题目来自于2000年的期末考试试题。考察卷积计算能力。

◎ 求解： 下面分别绘制出系统的单位冲激响应信号 $h\left( t \right)$ 与输入信号的波形。通过求解 $h\left( t \right) * x\left( t \right)$ 来获得系统零状态响应。

根据题目要求，将 $h\left( t \right)$ 进行反褶，准备进行卷积。
▲ 图1.6.12

根据 $h\left( t \right),x\left( t \right)$ 波形的特点，把卷积过程分成以下五个阶段。使用图解方法来确定每个阶段的积分上下限。

阶段1： $t < 0$

▲ 图1.6.13
在此阶段， $h\left( {t - \tau } \right),x\left( \tau \right)$ 之间没有重叠，所以 $h\left( t \right) * x\left( t \right) = 0$ 。

阶段2： $\le t < 1$

▲ 图1.6.14
在此阶段， $h\left( t \right),x\left( t \right)$ 之间有重叠，重叠区域为 $\tau \in \left( {0,t} \right)$ 。所以

$h\left( t \right) * x\left( t \right) = \int_0^t {e^{ - \left( {t - \tau } \right)} \cdot \tau \cdot d\tau } = e^{ - t} \int_0^t {\tau \cdot de^\tau }$ $e^{ - t} \cdot \left. {\left( {\tau \cdot e^\tau } \right)} \right|_0^t - e^{ - t} \int_0^t {e^\tau d\tau }$ $e^{ - t} \left( {t \cdot e^t - 0} \right) - e^{ - t} \cdot \left. {\left( {e^\tau } \right)} \right|_0^t$ $e^{ - t} \cdot \left( {e^t - 1} \right) = t - 1 + e^{ - t}$

阶段3： $\le t < 2$

▲ 图A1.6.15
在这个阶段， $h\left( t \right),x\left( t \right)$ 之间的重合区域为 $\tau \in \left( {t - 1,t} \right)$ 。这个区域计算卷积积分需要分成两个区间： $\left( {t - 1,1} \right)$ 和 $\left( {1,t} \right)$ 。

在区间 $\left( {t - 1,1} \right)$ 上的积分为

$\int_{t - 1}^1 {e^{ - \left( {t - \tau } \right)} \cdot \tau \cdot d\tau } = e^{ - t} \cdot \int_{t - 1}^1 {\tau de^\tau } = e^{ - t} \cdot \left. {\tau e^\tau } \right|_{t - 1}^1 - e^{ - t} \cdot \left. {e^\tau } \right|_{t - 1}^1$ $e^{ - t} \left[ {e^1 - \left( {t - 1} \right)^{e^{t - 1} } } \right] - e^{ - t} \left( {e^1 - e^{t - 1} } \right)$ $e^{1 - t} - t \cdot e^{ - 1} + e^{ - 1} - e^{1 - t} + e^{ - 1} = 2e^{ - 1} - t \cdot e^{ - 1}$

在区间 $\left( {1,t} \right)$ 上的积分为

$\int_1^t {e^{ - \left( {t - \tau } \right)} d\tau } = e^{ - t} \cdot \left. {e^\tau } \right|_1^t = e^{ - t} \left( {e^t - e^1 } \right) = 1 - e^{1 - t}$

将上面两部分合并在一起，卷积结果为

$h\left( t \right) * x\left( t \right) = 1 + 2e^{ - 1} - t \cdot e^{ - 1} - e^{1 - t}$

阶段4： $\le t < 3$

▲ 图1.6.16
在这个阶段， $h\left( t \right),x\left( t \right)$ 之间的重叠区域为 $\tau \in \left( {t - 1,2} \right)$ 。卷积积分为

$\int_{t - 1}^2 {e^{ - \left( {t - \tau } \right)} d\tau } = e^{ - t} \cdot \left. {e^\tau } \right|_{t - 1}^2 = e^{ - t} \cdot \left( {e^2 - e^{t - 1} } \right) = e^{2 - t} - e^{ - 1}$

阶段5： $t > 3$

▲ 图1.6.17

在此阶段， $h\left( t \right),x\left( t \right)$ 之间没有重合，卷积结果等于0。

综合上面五个阶段的卷积结果，可以的得到：

$h\left( t \right) * x\left( t \right) = \left\{ \begin{matrix} {0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t < 0}\\{t - 1 + e^{ - t} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \le t < 1}\\{1 + 2e^{ - 1} - t \cdot e^{ - 1} - e^{1 - t} ,\,\,\,\,1 \le t < 2}\\{e^{2 - t} - e^{ - 1} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2 \le t < 3}\\{0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t \ge 3}\\\end{matrix} \right.a$

下面利用Python程序绘制上述两个信号的卷积结果。

t = linspace(-0.5, 3.5, 500)

value = ((t-1+exp(-t))*(heaviside(t,0.5)-heaviside(t-1,0.5)) +
         (1+2*exp(-1)-t*exp(-1)-exp(1-t))*(heaviside(t-1,0.5)-heaviside(t-2,0.5)) +
         (exp(2-t)-exp(-1))*(heaviside(t-2,0.5)-heaviside(t-3,0.5)))

plt.plot(t, value)

plt.xlabel("t")
plt.ylabel("h(t)*x(t)")
plt.grid(True)
plt.tight_layout()
plt.show()

绘制的卷积结果为：

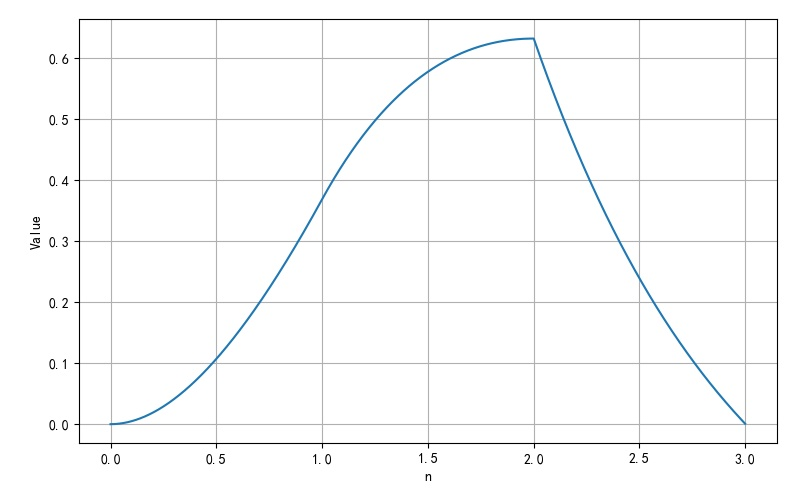
为了验证求取的函数表达式是否正确，下面使用数值积分来求解 $x\left( t \right) * h\left( t \right)$ 。

x = list([1]*500*linspace(0,1,500,endpoint=True)) + [1]*500
h = exp(-linspace(0,1,500,endpoint=True))
xh = convolve(x,h)/500
plt.plot(linspace(0,3,1499,endpoint=True), xh)

plt.xlabel("n")
plt.ylabel("Value")
plt.grid(True)
plt.tight_layout()
plt.show()

下面显示了数值求解的波形，对比可以看到与前面理论推导对应的信号波形是一致的。

在这里插入图片描述

最后一道题，如果需要降低难度，可以把 $h\left( t \right)$ 修改成方波： $h\left( t \right) = u\left( t \right) - u\left( {t - 1} \right)$ ，整个求解过程就会降低很大的难度。

■ 相关文献链接:

信号与系统2022年期末考试命题

一、命题要求

1、命题题型

2、命题内容覆盖分析

3、考试相关内容

（1）考试时间地点

（2）成绩录入

4、网络考试须知

§01 考试命题

一、选择题

二、判断对错

三、填空题

四、简答题

1、匹配滤波器

2、因果系统条件

3、频率泄露

五、计算题

1、傅里叶反变换

2、拉普拉斯变换

3、z反变换

4、离散傅里叶变换

5、求系统函数

六、系统分析

七、信号处理频谱分析

八、卷积运算

猜你喜欢