机器学习笔记 - 监督学习备忘清单

一、监督学习简介

给定一组数据点 $\{x^{(1)}, ..., x^{(m)}\}$ 关联到一组结果 $\{y^{(1)}, ..., y ^{(m)}\}$ ，我们想要构建一个分类器，学习如何从 $x$ 预测 $y$ 。

1、预测类型

下表总结了不同类型的预测模型：

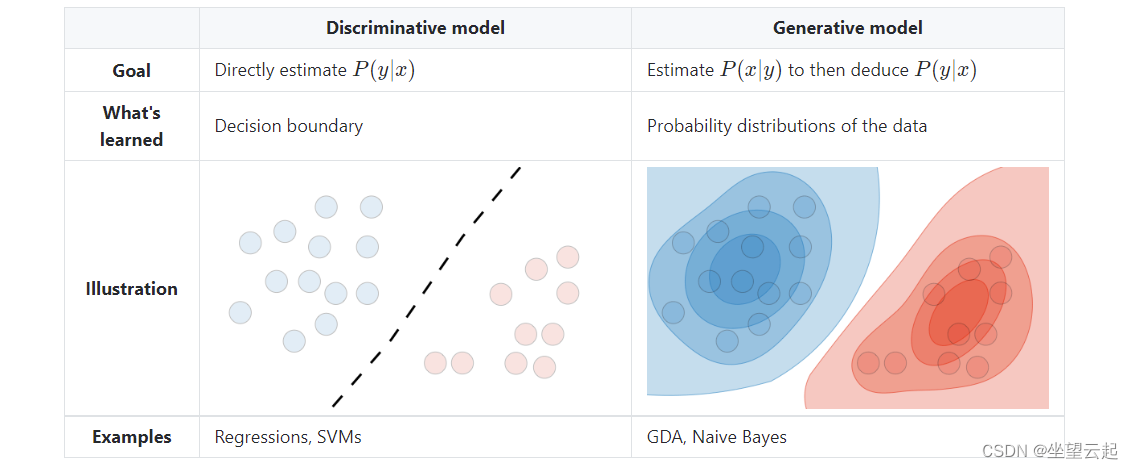
2、模型类型

下表总结了不同的模型：

二、符号和一般概念

1、Hypothesis

该假设被标记为 $h_\theta$ 并且是我们选择的模型。对于给定的输入数据 $x^{(i)}$ ，模型预测输出为 $h_\theta(x^{(i)})$ 。

2、Loss function

损失函数是一个函数 $L:(z,y)\in\mathbb{R}\times \longmapsto L(z,y)\in\mathbb{R}$ ，它将与真实数据值 $y$ 对应的预测值 $z$ 作为输入，并输出它们的差异程度。下表总结了常见的损失函数：

3、Cost function

成本函数 $J$ 通常用于评估模型的性能，其损失函数 $L$ 定义如下：

$\boxed{J(\theta)=\sum_{i=1}^mL(h_\theta(x^{(i)}), y^{(i)})}$

4、Gradient descent

通过注意 $\alpha\in\mathbb{R}$ 学习率，梯度下降的更新规则用学习率和成本函数 $J$ 表示如下：

$\boxed{\theta\longleftarrow\theta-\alpha\nabla J(\theta)}$

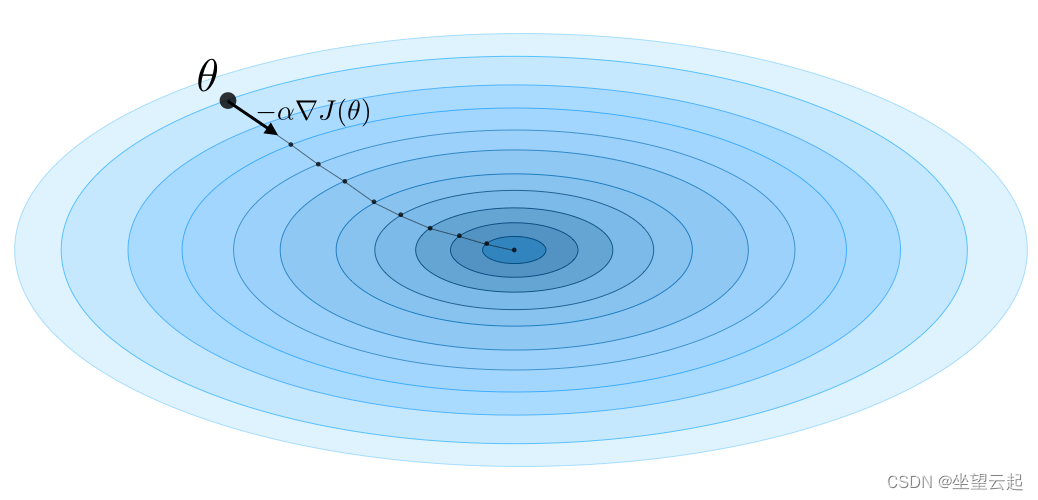
备注：随机梯度下降（SGD）是根据每个训练样例更新参数，批梯度下降是在一批训练样例上进行的。

5、Likelihood

给定参数 $\theta$ 的模型 $L(\theta)$ 的似然性用于通过似然最大化来找到最优参数 $\theta$ 。我们有：

$\boxed{\theta^{\textrm{opt}}=\underset{\theta}{\textrm{arg max }}L(\theta)}$

备注：在实践中，我们使用更容易优化的对数似然 $\ell(\theta)=\log(L(\theta))$ 。

6、Newton's algorithm

牛顿算法是一种求 $\theta$ 的数值方法，使得 $\ell'(\theta)=0$ 。其更新规则如下： $\boxed{\theta\leftarrow\theta-\frac{\ell'(\theta)}{\ell''(\theta)}}$

备注：多维泛化，也称为Newton-Raphson方法，有如下更新规则：

$\theta\leftarrow\theta-\left(\nabla_\theta^2\ell(\theta)\right)^{-1}\nabla_\theta\ell(\theta)$

三、线性模型

1、线性回归

我们在这里假设 $y|x;\theta\sim\mathcal{N}$

（1）Normal equations

通过注意设计矩阵 $X$ ，最小化成本函数的 $\theta$ 的值是一个封闭形式的解决方案，使得：

$\boxed{\theta=(X^TX)^{-1}X^Ty}$

（2）LMS algorithm

通过注意 α 学习率，最小均方 (LMS) 算法对 m 数据点的训练集的更新规则，也称为 Widrow-Hoff 学习规则，如下所示：

$\boxed{\forall j,\quad \theta_j \leftarrow \theta_j+\alpha\sum_{i=1}^m\left[y^{(i)}-h_\theta(x^{(i)})\right]x_j^{(i)}}$

备注：更新规则是梯度上升的特例。

（3）LWR

局部加权回归，也称为 LWR，是线性回归的一种变体，它通过 $w^{(i)}(x)$ 在其成本函数中对每个训练样例进行加权，它由参数 $\tau \in\mathbb{R}$ 定义为：

$\boxed{w^{(i)}(x)=\exp\left(-\frac{(x^{(i)}-x)^2}{2\tau^2}\right)}$

2、分类和逻辑回归

（1）Sigmoid 函数

sigmoid函数 $g$ ，也称为逻辑函数，定义如下： $\forall z\in\mathbb{R},\quad\boxed{g(z)=\frac{1}{1+e^{-z}}\in[0,1]}$

（2）Logistic regression

我们在这里假设 $y|x;\theta\sim\textrm{Bernoulli} (\phi)$ 。我们有以下形式：

$\boxed{\phi=p(y=1|x;\theta)=\frac{1}{1+\exp(-\theta^Tx)}=g(\theta^Tx)}$

备注：逻辑回归没有封闭形式的解决方案。

（3）Softmax regression

当有超过 2 个结果类别时，softmax 回归，也称为多类逻辑回归，用于泛化逻辑回归。按照惯例，我们设置 $\theta_K=0$ ，这使得每个类 $i$ 的伯努利参数 $\phi_i$ 为：

$\boxed{\displaystyle\phi_i=\frac{\exp(\theta_i^Tx)}{\displaystyle\sum_{j=1}^K\exp(\theta_j^Tx)}}$

3、广义线性模型

（1）Exponential family

如果一类分布可以用自然参数（也称为规范参数或链接函数）、 $\eta$ 、充分统计量 $T(y)$ 和对数来编写，则称它属于log-partition函数 $a(\eta)$ 如下：

$\boxed{p(y;\eta)=b(y)\exp(\eta T(y)-a(\eta))}$

备注：我们经常会有 $T(y)=y$ 。此外， $\exp(-a(\eta))$ 可以被视为一个标准化参数，它将确保概率总和为1。

下表总结了最常见的指数分布：

（2）Assumptions of GLMs

广义线性模型 (GLM) 旨在预测随机变量 $y$ 作为 $x\in\mathbb{R}^{n+1}$ 的函数，并依赖于以下 3 个假设：

(1) $\quad\boxed{y|x;\theta\sim\textrm{ExpFamily}(\eta)}$ (2) $\quad\boxed{h_\theta(x)=E[y|x;\theta]}$ (3) $\boxed{\eta=\theta^Tx}$

备注：普通最小二乘法和逻辑回归是广义线性模型的特例。

四、支持向量机

支持向量机的目标是找到与直线的最小距离最大的直线。

1、Optimal margin classifier

最佳边距分类器 $h$ 是这样的： $\boxed{h(x)=\textrm{sign}(w^Tx-b)}$ ，其中 $(w, b)\in\mathbb{R}^n\times\mathbb{R}$ 是以下优化问题的解： $\boxed{\min\frac{1}{2}||w||^2}\quad\quad\textrm{such that }\quad \boxed{y^{(i)}(w^Tx^{(i)}-b)\geqslant1}$

备注：决策边界定义为 $\boxed{w^Tx-b=0}$

2、Hinge loss

hinge loss用于 SVM 的设置，定义如下： $\boxed{L(z,y)=[1-yz]_+=\max(0,1-yz)}$

3、Kernel

给定一个特征映射 $\phi$ ，我们将内核 $K$ 定义如下： $\boxed{K(x,z)=\phi(x)^T\phi(z)}$

在实践中，由 $K(x,z)=\exp\left(-\frac{||x-z||^2}{2\sigma^2}\right)$ 定义的核 $K$ 称为高斯核，较常用。

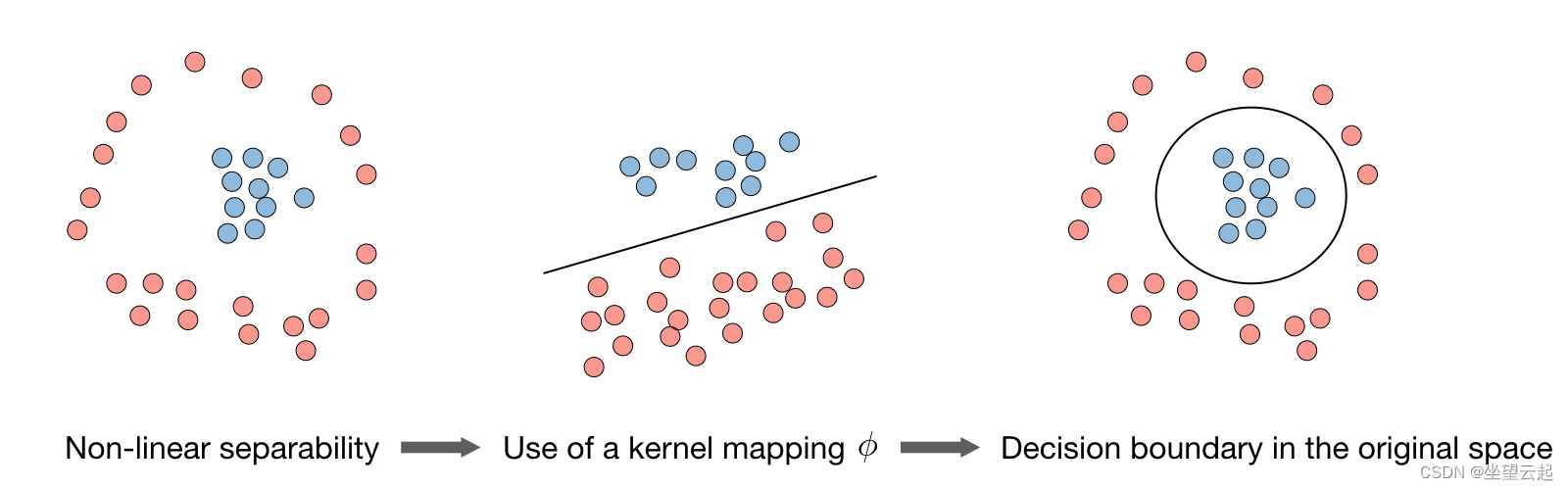
备注：我们说我们使用“内核技巧”来使用内核计算成本函数，因为我们实际上不需要知道显式映射 $\phi$ ，这通常非常复杂。相反，只需要值 $K(x,z)$ 。

4、Lagrangian

我们将拉格朗日 $\mathcal{L}(w,b)$ 定义如下： $\boxed{\mathcal{L}(w,b)=f(w)+\sum_{i=1}^l\beta_ih_i(w)}$

备注：系数 $\beta_i$ 称为拉格朗日乘数。

五、生成学习

生成模型首先尝试通过估计 $P(x|y)$ 来学习如何生成数据，然后我们可以使用贝叶斯估计 $P(y|x)$ 规则。

1、Gaussian Discriminant Analysis

（1）Setting

高斯判别分析假设 $y$ 和 $x|y=0$ 和 $x|y=1$ 是这样的：
(1) $\quad\boxed{y\sim\textrm{Bernoulli}(\phi)}$ (2) $\quad\boxed{x|y=0\sim\mathcal{N}(\mu_0,\Sigma)}$ (3) $\quad\boxed{x|y=1\sim\mathcal{N}(\mu_1,\Sigma)}$

（2）Estimation

下表总结了我们在最大化似然性时发现的估计值：

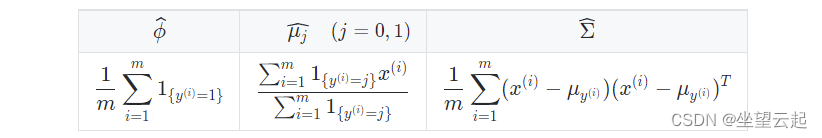
2、Naive Bayes

（1）Assumption

朴素贝叶斯模型假设每个数据点的特征都是独立的：

$\boxed{P(x|y)=P(x_1,x_2,...|y)=P(x_1|y)P(x_2|y)...=\prod_{i=1}^nP(x_i|y)}$

（2）Solutions

最大化对数似然给出以下解决方案：

$\boxed{P(y=k)=\frac{1}{m}\times\#\{j|y^{(j)}=k\}}\quad\textrm{ and }\quad\boxed{P(x_i=l|y=k)=\frac{\#\{j|y^{(j)}=k\textrm{ and }x_i^{(j)}=l\}}{\#\{j|y^{(j)}=k\}}}$

$k\in\{0,1\} , l\in[\![1,L]\!]$

备注：朴素贝叶斯广泛用于文本分类和垃圾邮件检测。

六、基于树和集成方法

这些方法可用于回归和分类问题。

1、CART

分类和回归树（CART），俗称决策树，可以表示为二叉树。它们的优点是易于解释。

2、Random forest

它是一种基于树的技术，它使用由随机选择的特征集构建的大量决策树。与简单的决策树相反，它是高度不可解释的，但其普遍良好的性能使其成为一种流行的算法。备注：随机森林是一种集成方法。

3、Boosting

提升方法的想法是将几个弱学习器组合成一个更强的学习器。主要的总结如下表：

Adaptive boosting	Gradient boosting
• High weights are put on errors to improve at the next boosting step • Known as Adaboost	• Weak learners are trained on residuals • Examples include XGBoost

七、其他非参数方法

1、k-nearest neighbors

k-最近邻算法，通常称为 k-NN，是一种非参数方法，其中数据点的响应由训练集中的 k 个邻居的性质决定。它可以用于分类和回归设置。

注：参数 k 越高，偏差越大，参数 k 越低，方差越高。

八、学习理论

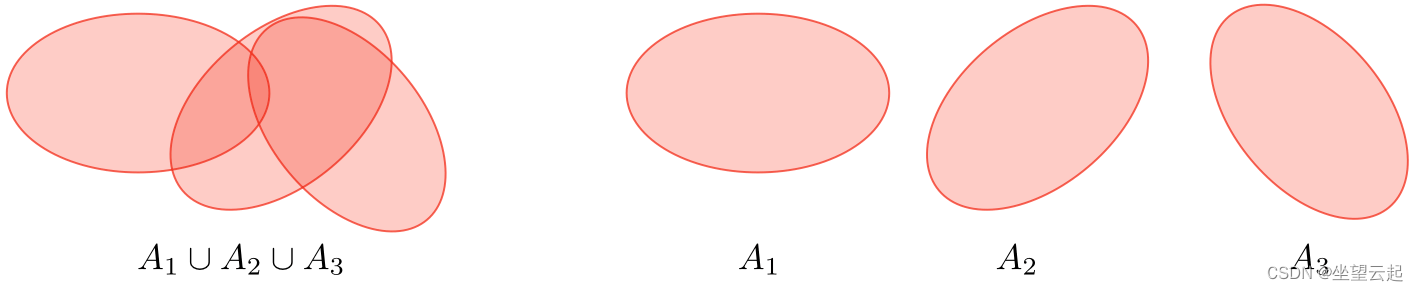
1、Union bound

令 $A_1, ..., A_k$ 为 k 个事件。我们有： $\boxed{P(A_1\cup ...\cup A_k)\leqslant P(A_1)+...+P(A_k)}$

2、Hoeffding inequality

令 $Z_1, .., Z_m$ 是从参数 $\phi$ 的伯努利分布中提取的 m iid 变量。设 $\widehat{\phi}$ 为他们的样本均值，并且 $\gamma>0$ 固定。我们有： $\boxed{P(|\phi-\widehat{\phi}|>\gamma)\leqslant2\exp(-2\gamma^2m)}$

备注：这个不等式也称为切尔诺夫界。

3、Training error

对于给定的分类器 h，我们定义训练误差 $\widehat{\epsilon}(h)$ ，也称为经验风险或经验误差，如下：

$\boxed{\widehat{\epsilon}(h)=\frac{1}{m}\sum_{i=1}^m1_{\{h(x^{(i)})\neq y^{(i)}\}}}$

4、Probably Approximately Correct (PAC)

PAC 是一个框架，在此框架下证明了学习理论的许多结果，并具有以下一组假设：

训练集和测试集遵循相同的分布

训练样例是独立绘制的

5、Shattering

给定一个集合 $S=\{x^{(1)},...,x^{(d)}\}$ 和一组分类器 $\mathcal{H}$ ，我们说 $\mathcal{H}$ 对于 $S$ 如果对于任何一组标签 $\{y^{(1)}, ..., y^{(d)}\}$ ，我们有： $\boxed{\exists h\in\mathcal{H}, \quad \forall i\in[\![1,d]\!],\quad h(x^{(i)})=y^{(i)}}$

6、Upper bound theorem

令 $\mathcal{H}$ 是一个有限假设类，使得 $|\mathcal{H}|=k$ 并且令 $\delta$ 和样本大小 $m$ 是固定的。然后，以至少 $1-\delta$ 的概率，我们有：

$\boxed{\epsilon(\widehat{h})\leqslant\left(\min_{h\in\mathcal{H}}\epsilon(h)\right)+2\sqrt{\frac{1}{2m}\log\left(\frac{2k}{\delta}\right)}}$

7、VC dimension

给定无限假设类 $\mathcal{H}$ 的 Vapnik-Chervonenkis (VC) 维数，记为 $\textrm{VC} (\mathcal{H})$ 是被 $H$ 打散的最大集合的大小。

注： ${\small\mathcal{H}=\{\textrm{set of linear classifiers in 2 dimensions}\}}$ 的VC维数为3。

8、Theorem (Vapnik)

设 $\mathcal{H}$ ， $\textrm{VC}(\mathcal{H})=d$ 和 $m$ 是训练样本的数量。以至少 $1-\delta$ 的概率，我们有：

$\boxed{\epsilon(\widehat{h})\leqslant \left(\min_{h\in\mathcal{H}}\epsilon(h)\right) + O\left(\sqrt{\frac{d}{m}\log\left(\frac{m}{d}\right)+\frac{1}{m}\log\left(\frac{1}{\delta}\right)}\right)}$