八、线性规划顶点、极值点和基本可行解决方案

1、基本可行方案

假设我们正在求解方程形式的一般线性程序：

这里， $A$ 是一个 $n \times m$ 的矩阵， $b \in R^m$ ， $c \in R^n$ ，今天，我们将假设 $A$ 的行是线性独立的。（如果不是，那么系统 $Ax = b$ 没有解，或者某些方程是多余的。在第一种情况下，我们只是忘记分析这样的线性程序；在第二种情况下，我们可以从删除冗余行。）

我们已经非正式地说过，基本可行的解决方案是“尽可能多的变量”为0。这不是很精确：在某些情况下（由于退化），可能有异常多的0值，并且我们不希望这与我们的定义混淆。相反，我们进行如下定义。

选择一些列（或变量） $B$ 的 $m-tuple$ 做为基本。我们希望 $B$ 是有序的，因为当以不同的顺序选择基本变量时，我们的表看起来会略有不同。为方便起见，我们让 $N$ 是非基本变量的 (n - m) 元组：那些不在 $B$ 中的变量。

我们可以将向量和矩阵分为基本部分和非基本部分。举个例子，如果 $x = (x_1, x_2, x_3, x_4, x_5 )$ ， $B = (2, 4)$ ， $N = (1, 3, 5)$ ，我们有 $X_B = (x2, x4)$ ，并且 $X_N = (x1, x3, x5)$ ，这也可以用 A 和 c 来完成：我们可以将目标函数写为 $c^TX = cB^TX_B + cN^TX_N$ ，方程组 $Ax = b$ 为 $A_BX_B + A_NX_N = b$ 。

为了得到一个基本的解决方案，我们要选择 $B$ 使得 $A_B$ （一个 $m \times m$ 矩阵）是可逆的。如果 A 的行是线性独立的，这总是可能的。并非 $B$ 的每一个选择都有效：例如，在二维中，如果可行域的两条边是平行线，则它们永远不会相交。

现在设置 $X_N = 0$ ，并且 $X_B = A^{-1}_B b$ 。这满足 $Ax = b$ 。此外，如果我们有 $X_B \geq 0$ （总是有 $X_N \geq 0$ ，因为 $X_N = 0$ ），我们称 x 为基本可行解。

2、角点的其他概念

除了基本可行的解决方案之外，还有其他的“角点”概念。我们说

集合 $S \subseteq \mathbb{R}^n$ 的一个顶点是一个点 $X \in S$ 使得某个线性函数 $\alpha ^Tx$ 在 $x$ 处严格最小化：对于任何 $y \in S$ ， $y \neq x$ ； $\alpha ^Tx < \alpha ^Ty$ 。

集合 $S \subseteq \mathbb{R}^n$ 的极值点是不位于 $S$ 的任何其他点之间的点 $X \in S$ 。形式上，如果 $x$ 是极值点，只要 $x \in [y, {y}']$ 对于 $y$ ； ${y}' \in S$ ， $x = y$ 或 $x = {y}'$ 。

换句话说，如果 $x$ 可以写成 $ty +(1-t){y}'$ 对于 y； ${y}' \in S$ 和 $0 \leq t \leq 1$ ，或者 $x = y$ （我们可以设置 $t = 1$ ）或 $x = {y}'$ （我们可以设置 $t = 0$ ）。

当我们考虑的集合是 $F = \{x \in \mathbb{R}^n : Ax = b, x\geq 0\}$ ，线性规划的可行域，三个概念基本可行解，顶点，极值点都相同。这就是我们今天要尝试证明的。

（1）从基本可行解到顶点

命题 2.1。任何基本可行解都是可行域的一个顶点。

证明。任意选择基本和非基本变量 $(B, N)$ ，设置 $X_N = 0$ 会产生基本可行解。定义 $\alpha$

那么 $a^Tx$ 是 x 中非基本变量的总和。由于 $X_N = 0$ ，当我们设置 $X_N = 0$ 时， $a^Tx$ 被最小化。这正是对应于 $(B, N)$ 的基本可行解。

（2）从顶点到极值点

命题 2.2。集合 $S \subseteq \mathbb{R}^n$ 的任何顶点也是 $S$ 的极值点。（特别是，任何基本可行解也是可行域的极值点。）

证明。令 $x \in S$ 是 $S$ 的一个顶点，并且 $\alpha$ 是向量使得对于任何 $y \in S$ 和 $y \neq x$ ， $a^Tx < a^Ty$ 。

假设 $x$ 位于线段 $[y, {y}']$ 与 $y$ ； $y \in S$ ； ${y}' \neq x$ 。这就是不成为极端的点。

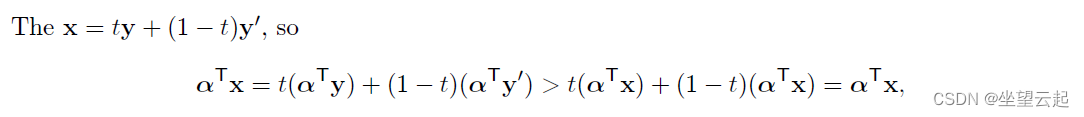使用不等式 $a^Tx < a^Ty$ 和 $a^Tx < a^T{y}'$ ，是矛盾的，因此 x 必须是一个极值点。。

（3）从极端点到基本可行的解决方案

最后一步，从极端点到基本可行的解决方案，是比较棘手的。

命题 2.3。可行域的任何极值点都是基本可行解。

证明。令 $x$ 为可行域的任意极值点。定义 $W = \{i : x_i \neq 0 \}$ 和 $\mathbb{Z} = \{i : x_i = 0 \}$ ，类比 B 和 N 以获得基本的可行解。

我们不能真正问 $A_W$ 是否可逆，因为我们甚至没有理由认为它是正方形的。但是我们可以做的是问我们是否可以找到一个非零的 $u \in R^n$ 使得：

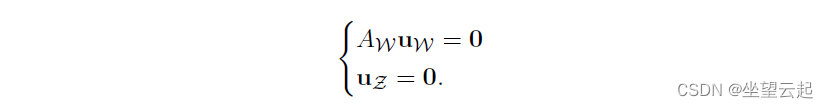
如果没有这样的 u，那么我们将认为 x 是一个基本可行的解决方案。如果有这样一个 u，那么我们将论证 x 实际上不是一个极值点，并产生矛盾。

现在，让 N 是 B 的补码。因为我们从 W 开始并可能将其变大来找到 B，所以我们知道 N 是通过从 Z 开始并可能使其变小来找到的。因为 $x_Z = 0$ （这就是我们选择 Z 的方式），所以我们也知道 $x_N = 0$ 。

现在我们快完成了。 $Ax = A_Bx_B + A_Nx_N = b$ 。由于 $x_N = 0$ ，我们有 $A_Bx_B = b$ ，所以 $x_B = A^{-1}_B b$ 。这正是我们想要的基本解决方案。

其次，假设存在这样一个 u。然后我们有

这意味着 $x+tu$ 形式的点仍然满足方程组：即 $A(x+tu) =b + t0 = b$ 。

并非所有 $x + tu$ 形式的点都是可行的：对于某些 t，我们可以找到一个坐标 i，使得 $x_i + tu_i < 0$ 。但是，我们知道这样的 i 必须在 W，而不是 Z，因为对于任何 $i \in Z$ ，我们有 $x_i = u_i = 0$ 。所以 $x_i > 0$ 。这意味着当 $\left | t \right |$ 足够小时， $x_i + tu_i > 0$ 也是如此。

选择一个足够小的 $t > 0$ 使得 $x+tu$ 和 $x-tu$ 都是可行的：对于每个 i， $x_i +tu_i > 0$ 和 $x_i - tu_i > 0$ 。这很像旋转：对于每个 i 要求 $\left | t \right |< \frac{\left | x_i \right |}{\left | u_i \right |}$ 满足 $u_i \neq 0$ 就足够了。

但是现在，x 位于从 $x + tu$ 到 $x - tu$ 的线段上。事实上，它是那条线段的中点。因为 $u \neq 0$ 且 $t > 0$ ，所以它不同于两个端点。所以 x 在这种情况下不是一个极值点，这与假设相反。