深入理解机器学习——机器学习模型的性能度量

分类目录：《深入理解机器学习》总目录

---

对学习器的泛化性能进行评估，不仅需要有效可行的实验估计方法，还需要有衡量模型泛化能力的评价标准，这就是性能度量（Performance Measure）。性能度量反映了任务需求，在对比不同模型的能力时，使用不同的性能度量往往会导致不同的评判结果；这意味着模型的“好坏”是相对的，什么样的模型是好的，不仅取决于算法和数据，还决定于任务需求。在预测任务中，给定样例集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯   , ( x m , y m ) } D=\{(x_1, y_1), (x_2, y_2), \cdots, (x_m, y_m)\} D={ (x1​,y1​),(x2​,y2​),⋯,(xm​,ym​)}，其中$y_i$是示例$x_i$的真实标记。要评估学习器$f$的性能，就要把学习器预测结果$f(x)$与真实标记$y$进行比较。

回归任务的性能度量

回归任务最常用的性能度量是“均方误差”（Mean Squared Error, MSE）：
$$E(f;D)=\frac{1}{m}\sum _{i=1}^m(f(x_i)-y_i{)}^2$$

更一般的，对于数据分布$D$和概率密度函数$p(\cdot )$，均方误差可描述为：
$$E(f;D)={\int }_{x\sim D}(f(x_i)-y_i{)}^{2}p(x)\text{d}x$$

分类任务的性能度量

错误率与准确率

《机器学习模型数据集的划分与模型评估方法》中提到了错误率和准确率，这是分类任务中最常用的两种性能度量既适用于二分类任务，也适用于多分类任务。错误率是分类错误的样本数占样本总数的比例，准确率则是分类正确的样本数占样本总数的比例。对样例集$D$，分类错误率定义为：
$$E(f;D)=\frac{1}{m}\sum _{i=1}^m\mathbb{I}(f(x_i)\ne y_i)$$

则准确率定义为：
$$\text{Accuracy}(f;D)=\frac{1}{m}\sum _{i=1}^m\mathbb{I}(f(x_i)=y_i)=1-E(f;D)$$

精度/查准率、召回率/查全率与F1度量

错误率和准确率虽常用，但并不能满足所有任务需求。错误率衡量了有多少比例的样本被判别错误，但是若我们关心的是“判定为正例的样本中有多少是正例”，或者“所有正例中有多少比例被判定出来”，那么错误率和准确率显然就不够用了，这时需要使用其他的性能度量类似的需求在信息检索、Web搜索等应用中经常出现，例如在信息检索中，我们经常会关心“检索出的信息中有多少比例是用户感兴趣的”“用户感兴趣的信息中有多少被检索出来了”，精度/查准率（Precision）与召回率/查全率（Recall）是更为适用于此类需求的性能度量。

对于二分类问题，可将样例根据其真实类别与学习器预测类别的组合划分为真正例（True Positive, TP）、假正例（False Positive, FP）、真反例（True Negative, TN）与假反例（False Negative, FN）四种情形，令TP、FP、TN、FN分别表示其对应的样例数，则显然有TP+FP+TN+FN=样例总数。分类结果的“混淆矩阵”（Confusion Matrix）如下图所示：

则精度/查准率（Precision）与召回率/查全率（Recall）被定义为：
$$\begin{gathered} \text{Precision}=\frac{TP}{TP+FP} \\ \text{Recall}=\frac{TP}{TP+FN} \end{gathered}$$

精度/查准率和召回率/查全率是一对矛盾的度量。一般来说，精度/查准率高时，召回率/查全率往往偏低；而召回率/查全率高时，精度/查准率往往偏低。例如，若希望将正例尽可能多地选出来，则可通过增加选择样本的数量来实现，如果将所有样本都选上，那么所有的正例也必然都被选上了，但这样精度/查准率就会较低；若希望选出的瓜中好瓜比例尽可能高，则可只挑选最有把握的样本，但这样就难免会漏掉不少正例，使得召回率/查全率较低。通常只有在一些简单任务中，才可能使召回率/查全率和精度/查准率都很高。

在很多情形下，我们可根据学习器的预测结果对样例进行排序，排在前面的是学习器认为“最可能”是正例的样本，排在最后的则是学习器认为“最不可能”是正例的样本。按此顺序逐个把样本作为正例进行预测，则每次可以计算出当前的召回率/查全率、精度/查准率。以精度/查准率为纵轴、召回率/查全率为横轴作图，就得到了精度/查准率召回率/查全率曲线，简称“PR曲线”，显示该曲线的图称为“P-R图”，下图给出了一个示意图：

PR图直观地显示出学习器在样本总体上的召回率/查全率、精度/查准率在进行比较时，若一个学习器的PR曲线被另一个学习器的曲线完全“包住”，则可断言后者的性能优于前者，例如上图中学习器A的性能优于学习器C；如果两个学习器的PR曲线发生了交叉，例如上图中的A与B，则难以一般性地断言两者孰优孰劣，只能在具体的精度/查准率或召回率/查全率条件下进行比较。然而，在很多情形下，人们往往仍希望把学习器A与B比出个高低。这时一个比较合理的判据是比较P-R曲线下面积的大小，它在一定程度上表征了学习器在精度/查准率和召回率/查全率上取得相对“双高”的比例。但这个值不太容易估算，因此，人们设计了一些综合考虑精度/查准率、召回率/查全率的性能度量“平衡点”（Break-Event Point，简称BEP）就是这样一个度量，它是“精度/查准率=召回率/查全率”时的取值，例如上图中学习器C的BEP是0.64，而基于BEP的比较，可认为学习器A优于B。

但BEP还是过于简化了些，更常用的是$F1$度量：
$$F1=\frac{2\times \text{Precision}\times \text{Recall}}{\text{Precision}+\text{Recall}}=\frac{2\times TP}{\text{样例总数}+TP-TN}$$

在一些应用中，对精度/查准率和召回率/查全率的重视程度有所不同。例如在商品推荐系统中，为了尽可能少打扰用户，更希望推荐内容确是用户感兴趣的，此时精度/查准率更重要；而在逃犯信息检索系统中，更希望尽可能少漏掉逃犯，此时召回率/查全率更重要。$F1$度量的一般形式是$F_{\beta }$，能让我们表达出对精度/查准率/召回率/查全率的不同偏好，它定义为：
$$F_{\beta }=\frac{(1+{\beta }^2)\times \text{Precision}\times \text{Recall}}{({\beta }^2\times \text{Precision})+\text{Recall})}$$

其中$\beta >0$度量了召回率/查全率对精度/查准率的相对重要性。$\beta =1$时退化为标准的$F1$；$\beta >1$时召回率/查全率有更大影响；$\beta <1$时精度/查准率有更大影响。

很多时候我们有多个二分类混淆矩阵，例如进行多次训练/测试，每次得到一个混淆矩阵；或是在多个数据集上进行训练/测试，希望估计算法的“全局”性能；甚或是执行多分类任务，每两两类别的组合都对应一个混淆矩阵等等。总之，我们希望在$n$个二分类混淆矩阵上综合考察精度/查准率和召回率/查全率。

一种直接的做法是先在各混淆矩阵上分别计算出精度/查准率和召回率/查全率，记为$(P_1,R_1),(P_2,R_2),\cdots ,(P_n,R_n),$，再计算平均值，这样就得到宏精度/查准率（Macro-Precision）、宏召回率/查全率（Macro-Recall），以及相应的宏$F1$（Macro-$F1$）：

$$\begin{gathered} \text{Macro-Precision}=\frac{1}{n}\sum _{i=1}^n{P}_i \\ \text{Macro-Recall}=\frac{1}{n}\sum _{i=1}^n{R}_i \\ \text{Macro-}F1=\frac{2\times \text{Macro-Precision}\times \text{Macro-Recall}}{\text{Macro-Precision}+\text{Macro-Recall}} \end{gathered}$$

还可先将各混淆矩阵的对应元素进行平均，得到TP、FP、TN、FN的平均值，分别记为$\overline{TP}$、$\overline{FP}$、$\overline{TN}$、$\overline{FN}$，再基于这些平均值计算出微精度/查准率（Micro-Precision）、微召回率/查全率（Micro-Recall）和微$F1$（Micro-$F1$）：
$$\begin{gathered} \text{Micro-Precision}=\frac{\overline{TP}}{\overline{TP}+\overline{FP}} \\ \text{Macro-Recall}=\frac{\overline{TP}}{\overline{TP}+\overline{FN}} \\ \text{Macro-}F1=\frac{2\times \text{Micro-Precision}\times \text{Micro-Recall}}{\text{Micro-Precision}+\text{Micro-Recall}} \end{gathered}$$

ROC（Receiver Operating Characteristic）与AUC（Area Under ROC Curve）

很多学习器是为测试样本产生一个实值或概率预测，然后将这个预测值与一个分类阈值进行比较，若大于阈值则分为正类，否则为反类。例如，神经网络在一般情形下是对每个测试样本预测出一个$[0,1]$之间的实值然后将这个值与0.5进行比较，大于0.5则判为正例，否则为反例。这个实值或概率预测结果的好坏，直接决定了学习器的泛化能力。实际上，根据这个实值或概率预测结果，我们可将测试样本进行排序，“最可能”是正例的排在最前面，“最不可能”是正例的排在最后面。这样，分类过程就相当于在这个排序中以某个“截断点”将样本分为两部分，前一部分判作正例，后一部分则判作反例。

在不同的应用任务中，我们可根据任务需求来采用不同的截断点，例如若我们更重视精度/查准率，则可选择排序中靠前的位置进行截断；若更重视召回率/查全率，则可选择靠后的位置进行截断。因此，排序本身的质量好坏，体现了综合考虑学习器在不同任务下的“期望泛化性能”的好坏，或者说“一般情况下泛化性能的好坏。ROC曲线则是从这个角度出发来研究学习器泛化性能的有力工具。

ROC全称是“受试者工作特征”（Receiver Operating Characteristic）曲线，它源于“二战”中用于敌机检测的雷达信号分析技术，二十世纪六七十年代开始被用于一些心理学、医学检测应用中，此后被引入机器学习领域，与上文中介绍的P-R曲线相似，我们根据学习器的预测结果对样例进行排序，按此顺序逐个把样本作为正例进行预测，每次计算出两个重要量的值，分别以它们为横、纵坐标作图，就得到了“ROC曲线”。与PR曲线使用精度/查准率、召回率/查全率为纵、横轴不同，ROC曲线的纵轴是“真正例率”（True Positive Rate，简称TPR），横轴是“假正例率”（False Positive Rate，简称FPR），基于前文中的符号，两者分别定义为：
$$\begin{gathered} TPR=\frac{TP}{TP+FN} \\ FPR=\frac{FP}{TN+FP} \end{gathered}$$

显示ROC曲线的图称为“ROC图”，下图给出了一个示意图，显然对角线对应于“随机猜测”模型，而点$(0,1)$则对应于将所有正例排在所有反例之前的“理想模型”：

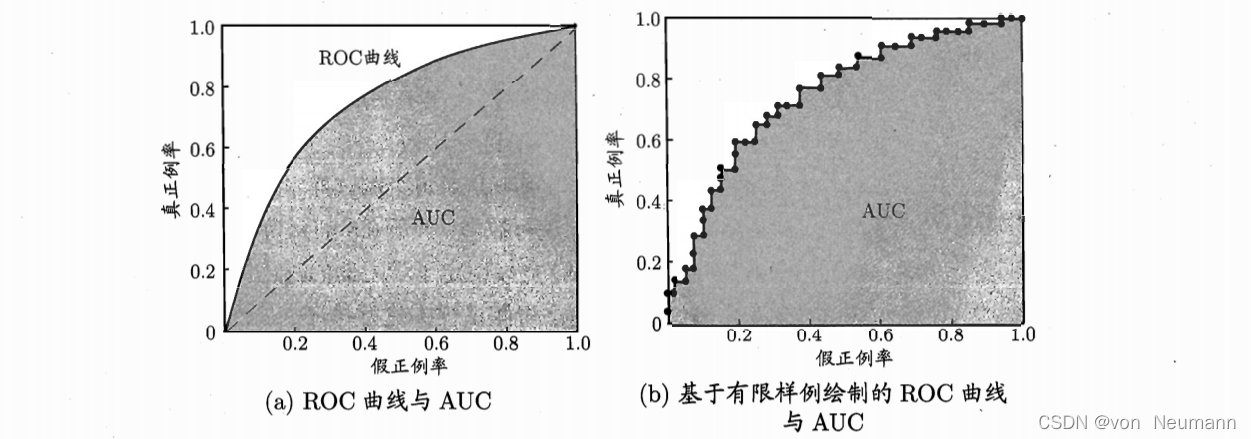
现实任务中通常是利用有限个测试样例来绘制ROC图，此时仅能获得有限个（真正例率，假正例率）坐标对，无法产生上图（a）中的光滑ROC曲线，只能绘制出如上图（b）所示的近似ROC曲线。绘图过程很简单：给定$m^{+}$个正例和$m^{-}$个反例，根据学习器预测结果对样例进行排序，然后把分类阈值设为最大，即把所有样例均预测为反例，此时真正例率和假正例率均为0，在坐标（0,0）处标记一个点。然后，将分类阈值依次设为每个样例的预测值，即依次将每个样例划分为正例。设前一个标记点坐标为$(x,y)$，当前若为真正例，则对应标记点的坐标为$(x,y+\frac{1}{m^{+}})$；当前若为假正例，则对应标记点的坐标为$(x+\frac{1}{m^{-}},y)$，然后用线段连接相邻点即得。

进行学习器的比较时，与PR图相似，若一个学习器的ROC曲线被另个学习器的曲线完全“包住”，则可断言后者的性能优于前者；若两个学习器的ROC曲线发生交叉，则难以一般性地断言两者孰优孰劣。此时如果一定要进行比较，则较为合理的判据是比较ROC曲线下的面积，即AUC（Area Under ROC Curve），如上图所示。

从定义可知，AUC可通过对ROC曲线下各部分的面积求和而得。假定ROC曲线是由坐标为 { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯   , ( x m , y m ) } \{(x_1, y_1), (x_2, y_2), \cdots, (x_m, y_m)\} { (x1​,y1​),(x2​,y2​),⋯,(xm​,ym​)}的点按序连接而形成，参见上图（b），则AUC可估算为：
$$\text{AUC}=\frac{1}{2}\sum _{i=1}^{m-1}(x_{i+1}-x_i)\times (y_i+y_{i+1})$$

形式化地看，AUC考虑的是样本预测的排序质量，因此它与排序误差有紧密联系。给定$m^{+}$个正例和$m^{-}$个反例，令$D^{+}$和$D^{-}$分别表示正、反例集合，则排序“损失”定义为：
$$l_{\text{rank}}=\frac{1}{m^{+}{m}^{-}}\sum _{x^{+}\in D^{+}}\sum _{x^{-}\in D^{-}}(\mathbb{I}(f(x^{+})<f(x^{-}))+\frac{1}{2}(\mathbb{I}(f(x^{+})=f(x^{-})))$$

即考虑每一对正、反例，若正例的预测值小于反例，则记一个“罚分”，若相等，则记0.5个“罚分”。容易看出，$l_{\text{rank}}$对应的是ROC曲线之上的面积：若一个正例在ROC曲线上对应标记点的坐标为$(x,y)$，则$x$恰是排序在其之前的反例所占的比例，即假正例率。因此有：
$$\text{AUC}=1-l_{\text{rank}}$$

代价敏感错误率与代价曲线

在现实任务中常会遇到这样的情况：不同类型的错误所造成的后果不同，例如在医疗诊断中，错误地把患者诊断为健康人与错误地把健康人诊断为患者，看起来都是犯了“一次错误”，但后者的影响是增加了进一步检查的麻烦，前者的后果却可能是丧失了拯救生命的最佳时机；再如，门禁系统错误地把可通行人员拦在门外，将使得用户体验不佳，但错误地把陌生人放进门内，则会造成严重的安全事故。为权衡不同类型错误所造成的不同损失，可为错误赋予“非均等代价”。

以二分类任务为例，我们可根据任务的领域知识设定一个“代价矩阵”，如下图所示，其中${\text{cost}}_{ij}$表示将第$i$类样本预测为第$j$类样本的代价。一般来说，${\text{cost}}_{ii}=0$；若将第0类判别为第1类所造成的损失更大，则${\text{cost}}_{01}>{\text{cost}}_{10}$；损失程度相差越大，${\text{cost}}_{01}$与${\text{cost}}_{10}$值的差别越大。

直接计算“错误次数”，并没有考虑不同错误会造成不同的后果。在非均等代价下，我们所希望的不再是简单地最小化错误次数，而是希望最小化总体代价。若将上图中的第0类作为正类、第1类作为反类，令$D^{+}$与$D^{-}$分别代表样例集$D$的正例子集和反例子集，则“代价敏感”（cost-sensitive）错误率为：
$$E(f;D;\text{cost})=\frac{1}{m}(\sum _{x_i\in D^{+}}\mathbb{I}(f(x_i)\ne y_i)\times {\text{cost}}_{01}+\sum _{x_i\in D^{-}}\mathbb{I}(f(x_i)\ne y_i)\times {\text{cost}}_{10})$$

类似的，可给出基于分布定义的代价敏感错误率，以及其他一些性能度量如精度的代价敏感版本。若令${\text{cost}}_{ij}$中的$i$、$j$取值不限于 { 0 , 1 } \{0, 1\} { 0,1}，则可定义出多分类任务的代价敏感性能度量在非均等代价下，ROC曲线不能直接反映出学习器的期望总体代价，而“代价曲线”则可达到该目的。代价曲线图的横轴是取值为$[0,1]$的正例概率代价：
$${\text{cost}}_{P(+)}=\frac{p\times {\text{cost}}_{01}}{p\times {\text{cost}}_{01}+(1-p)\times {\text{cost}}_{10}}$$

其中$p$是样例为正例的概率；纵轴是取值为$[0,1]$的归一化代价：
$${\text{cost}}_{\text{norm}}=\frac{FNR\times p\times {\text{cost}}_{01}+FPR\times (1-p)\times {\text{cost}}_{10}}{p\times {\text{cost}}_{01}+(1-p)\times {\text{cost}}_{10}}$$

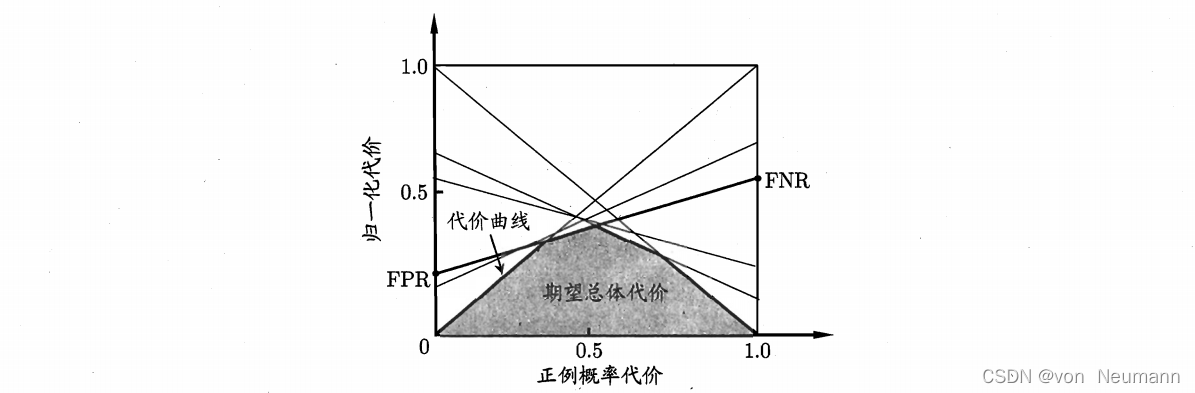
其中$FPR$是假正例率，$FNR=1-TPR$是假反例率。代价曲线的绘制很简单：ROC曲线上每一点对应了代价平面上的一条线段，设ROC曲线上点的坐标为$(TPR,FPR)$，则可相应计算出$FNR$，然后在代价平面上绘制一条从$(0,FPR)$到$(1,FNR)$的线段，线段下的面积即表示了该条件下的期望总体代价；如此将ROC曲线上的每个点转化为代价平面上的一条线段，然后取所有线段的下界，围成的面积即为在所有条件下学习器的期望总体代价，如下图所示：