基于simulink和adams的机械臂自适应控制

github地址

https://github.com/zzy5510/adaptive_arm_simulink

模型构建

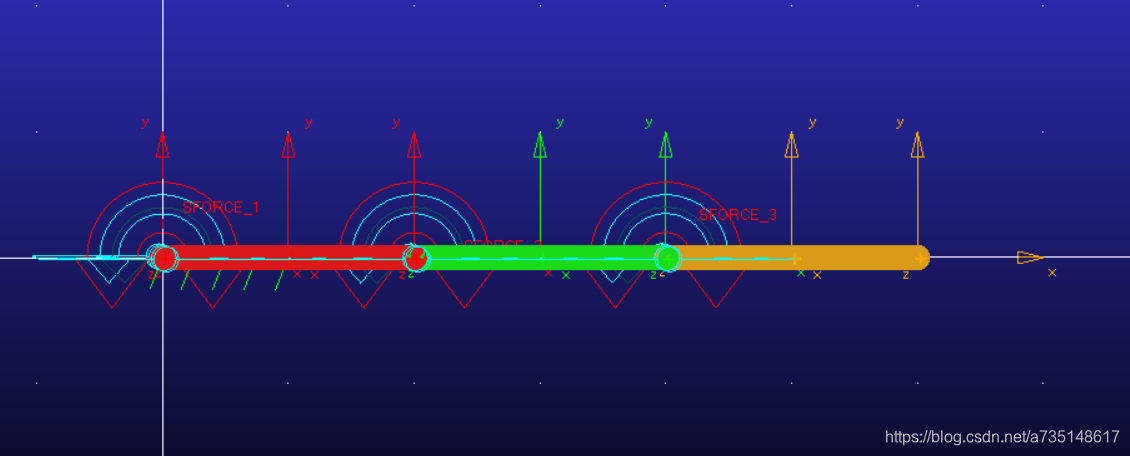
本想基于原来的七自由度机械臂做自适应控制，但发现自适应控制需要用到线性化的动力学参数矩阵，七自由度机械臂的参数矩阵太庞大和复杂了。所以新做了一个平面三自由度机械臂，如下图：
在这里插入图片描述
机械臂的质量均为10，z轴的惯量为1.05.

算法原理

欧拉拉格朗日法求动力学方程

首先，需要使用拉格朗日法求出机械臂的动力学方程：
$\ddot{q}+C(q, q) q+G(q)=\tau$
拉格朗日法的具体实现可以有不同的方法。本项目采用了霍伟《机器人动力学与控制》中的方法，比较便于编程实现。具体如下：
在这里插入图片描述

需要注意以下几点：
1.该方法不依赖于建系方法，即普通DH和改进DH都可应用。但推荐使用改进DH，因为公式中的连杆i质心的坐标是在i系中表达的，如果采用普通DH，这一坐标随关节角度将变化。
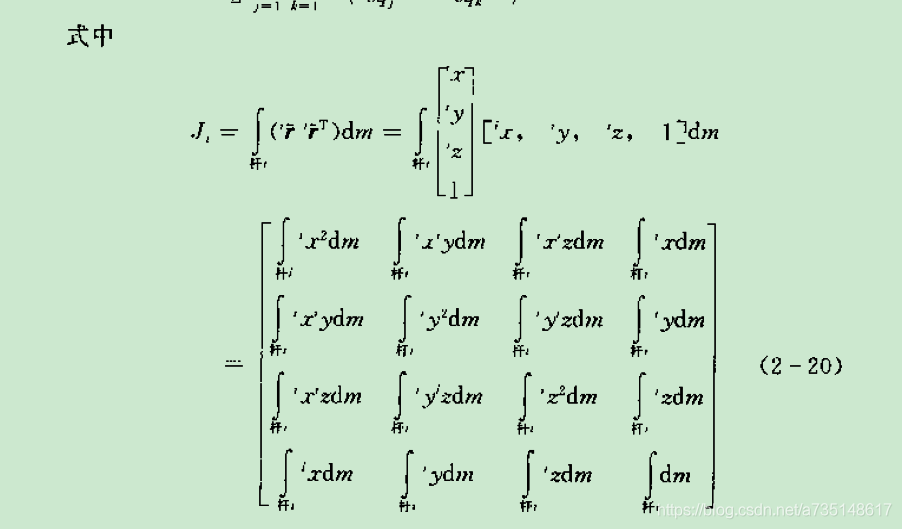
2.惯性张量I以坐标系的原点为原点，并不以杆的质心为原点。
这部分算法的代码来自https://www.jianshu.com/p/6d04539f1cfe。

自适应控制

本项目假定连杆3由于抓取了未知物体，质量和转动惯量变为未知。因此需要采用自适应算法来实现对机械臂的控制。算法的思路来自《漂浮基单_双臂空间机器人捕获目标过程接触碰撞动力学分析与镇定控制》
设定系统位置误差为
$e=q_{d}-q$
定义增广误差：
$s=\dot{e}+\lambda e$
定义参考输入角速度和角加速度：
$\eta =\dot{q}_{d}+\lambda e$
$\dot{\eta} =\ddot{q}_{d}+\lambda \dot{e}$
带入动力学表达式，得到：
$\dot{s}+Cs=H \ddot{\eta}+ C \dot{\eta}-\tau$
设计控制输入力矩为：
$\tau=\hat{H} \ddot{\eta}+ \hat{C} \dot{\eta}+Ks$
其中， $\hat{H}$ 和 $\hat{C}$ 代表对H和C的估计。将该式带入上式：
$\dot{s}+Cs+Ks=W\phi$
其中，
$W\phi=(H-\hat{H})\ddot{\eta}+(C-\hat{C})\dot{\eta}$
$\phi$ 是待估计的动力学参数的真实值与估计值的差组成的列向量，即为[m3;Iz3]。该公式实际上将动力学参数与运动学参数q， $\dot{q}$ , $\ddot{q}$ 的分离，完成了动力学参数的线性化。
最后，用自适应律：
$\phi=-\gamma W^{\mathrm{T}}s$
来更新动力学参数。关于自适应控制的稳定性证明略。

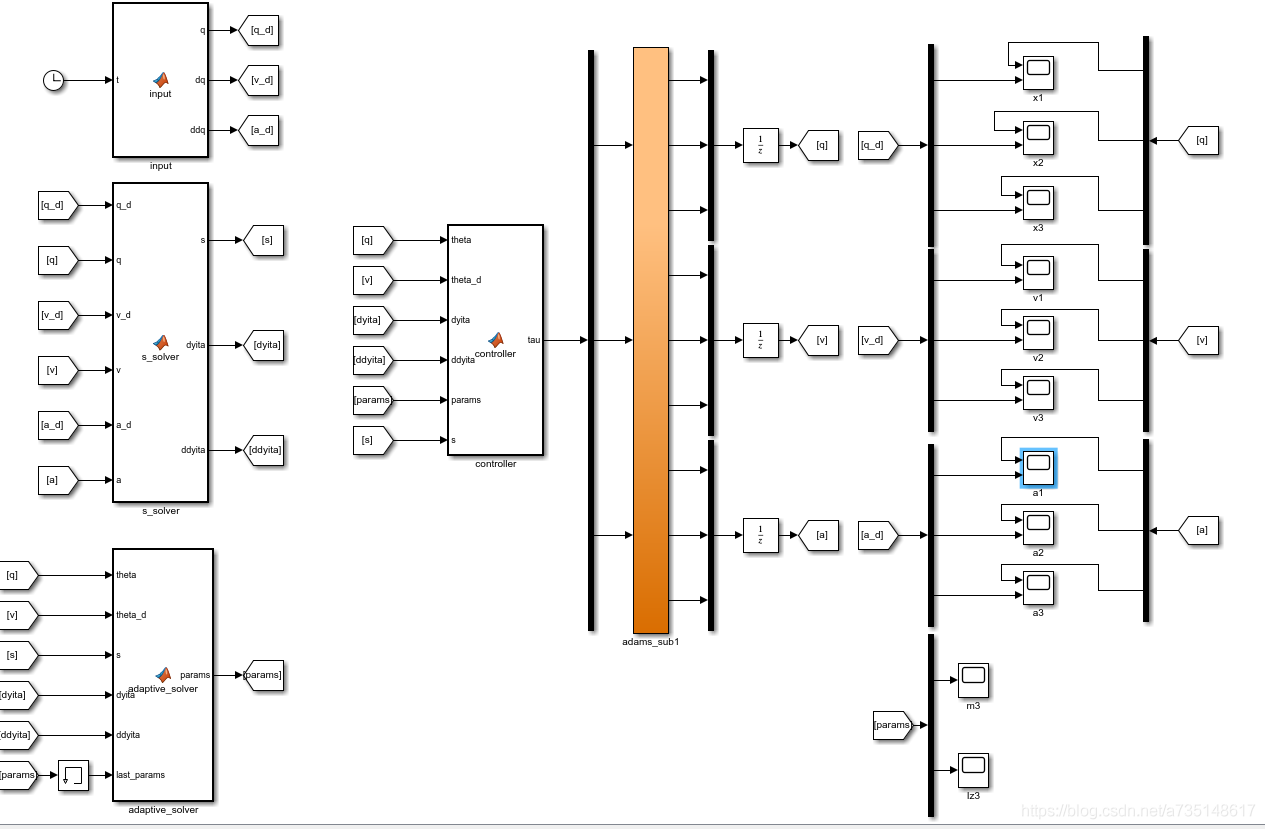
simulink控制图

在这里插入图片描述
四个函数分别为输入，s和 $\eta$ 的计算，自适应计算器，控制器。

运行效果

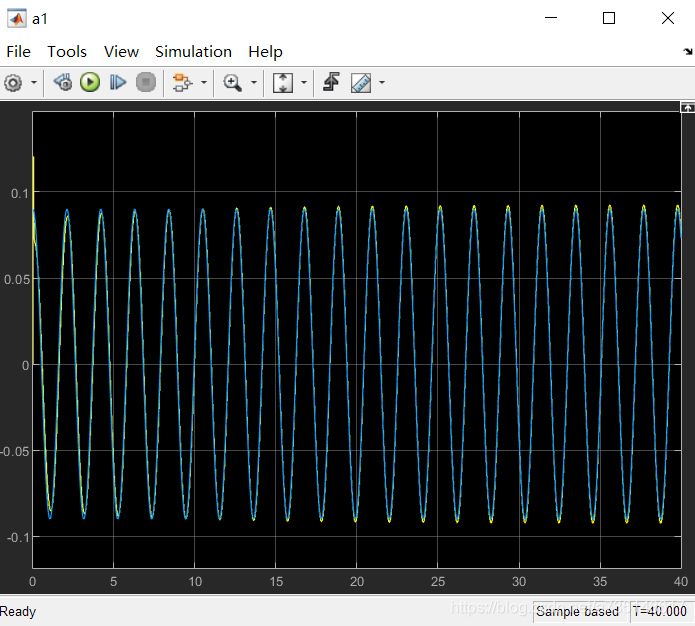
当输入为正弦信号时，机械臂运动跟踪效果如下：
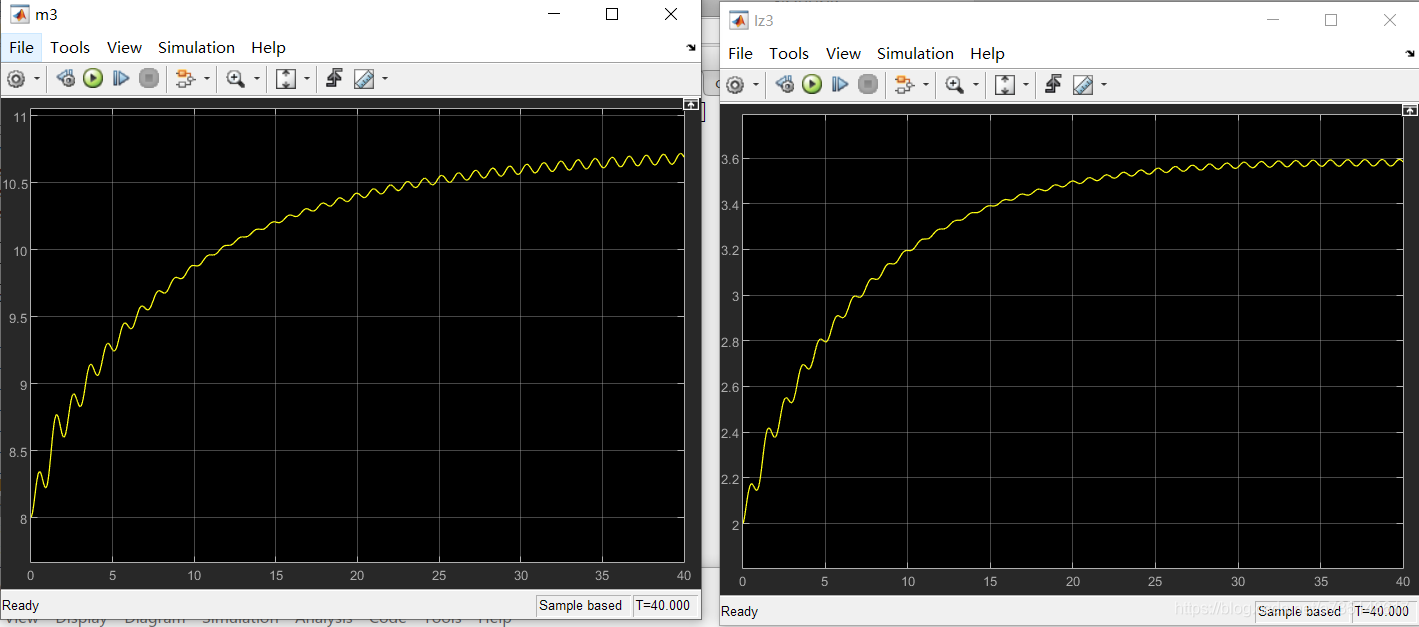
在这里插入图片描述
跟踪效果还是非常好的。然而，对参数的估计并没有收敛到真值：

这是因为正弦输入信号不满足持续激励（PE）条件。尽管输出可以收敛到真值，但参数估计却无法收敛到真值。这也是自适应控制的一大特点。
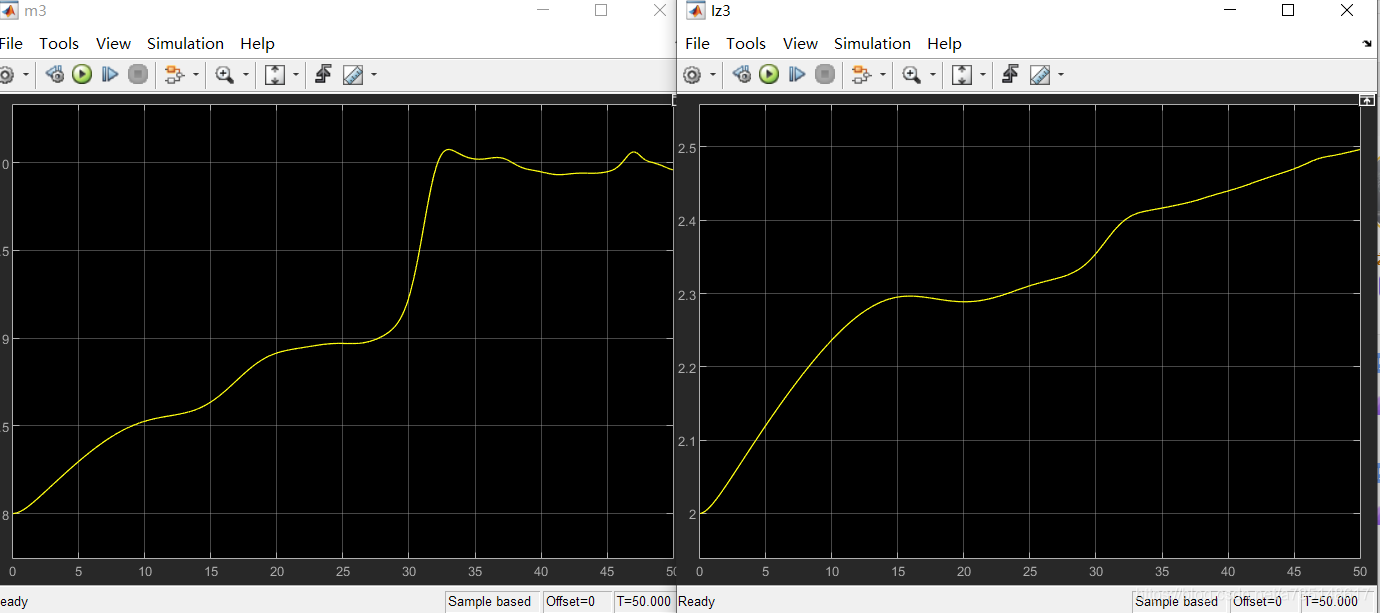
当输入恒加速度信号时，跟踪效果也不错。
在这里插入图片描述
然而，对参数的估计依然不收敛。非常迷惑，加速度信号理论上是满足PE条件的。多次调试后依然不收敛。这个问题先放在这里，以后解决吧。