首先，提出工程中实际存在的问题：
如果用一个高精度万用表去测量一个电源输出的直流电平，已知该电源的直流电平符合高斯分布，而每次观测，都用万用表等时间间隔采集N个点的数据，即：
其中：
对采集到的N个点数据，我们希望估计直流电平A，此时可以有无数个无偏估计的方法，下面随意举三种方法：
第一种估计方法：
即每次只取采集到的N个数据的第一个数据，估计直流电平A。此类系统可能在数据采集能力、存储深度等方面存在限制的系统中使用，因此只能选用一个采样点进行估计；
第二种估计方法：
即每次只取采集到的N个数据的第一个和最后一个数据，加权后估计直流电平A；此类系统，估计算法可以采用两个采样点，此时也提出了一种无偏估计。
第三种估计方法：
即对每次采集到的N个数据，利用其算术平均的结果，估计估计直流电平A。此类系统，可以采集N个观测数据，且N个观测数据都可以用于估计参数A。此时用的是算术平均的方法，当然在此条件下，还有采用各种的加权系数的无偏估计方法。
由于上述估计，都满足：
因此，都是关于A的无偏估计，满足估计无偏性条件。但这三个估计量哪个更加有效，那需要比较三个估计量的方差。
观察三种无偏估计的方差，可以得到：
因此，当
时，尽管三个都是无偏估计，但他们的方差满足：
因此，就这三种估计来说，显然
是最好的。
接下来我们仍然需要回答如下两个问题：
- 对于高斯噪声特性已知的情况下，无偏估计
的方差是否存在理论上的最小值？最小值是多少？也就是不管A采用哪种无偏估计，其方差都不可能低于这个极限；
- 是否存在一个最有效的估计量，使得该估计量的方差最小，也就是达到上个问题的方差最小值，此时我们就找到了该估计量的最小方差无偏估计。
针对问题1，由于
针对问题2，如果能够找到MVU，那么后续针对这一类工程中的问题，就可以一直使用该估计方法进行估计即可。因为针对此参数的其他无偏估计，其方差肯定不会低于MVU估计方法的方差。
想要回答上述问题，需要使用CRLB定理，首先阐述一下标量形式的CRLB定理
针对上述关于直流电平估计的例子，我们可以采用统计信号处理中的CRLB极限进行回答，先说结论：
如果要从采集到的一组观测量：
并利用其概率密度函数
(此时该函数被称为似然函数)去估计未知参数
时，如果
满足正则条件，即：
那么对参数
的任意无偏估计
的方差满足：
其中：
CRLB结论的作用一般有两个：
第一：在参数θ的无偏估计没有明确的情况下，就可以通过该公式确定此参数无偏估计方差的下限（被称为CRLB下限），也就是任意对参数
第二：在某些情况下，能够求出达到CRLB下限的最小方差无偏估计。
接下来，对标量形式的CRLB进行证明
在证明的过程中，会用到如下几个公式和定理：
首先是任意函数自然对数的导数满足：
因此，可以得到：
其次是Cauchy-Schwarz不等式，即：
该不等式成立的条件是：当存在某个与x无关的参数c，且满足：
上述不等式等号成立。
下面开始定理的证明：
首先我们讨论的是关于
的无偏估计
，因此可以从无偏估计的定义入手，即
其中
用观测到的一组数据
进行的某种无偏估计方法。然后我们对上式两边对θ进行求导，即：
除了当概率密度函数的非零域与未知参数
有关之外，上述求导和积分可以互换[1]。或者可以描述为上述数学期望的积分上下限与估计量
有关，那么求导与积分就不能互换，因此就不能使用正则条件。
对求导与积分互换后，我们得到：
而其中
中不包含参数
，因此进一步可以得到：
使用上述自然对数导数的性质，可以得到：
因此：
利用正则条件，此时有：
两边都乘
后可以得到：
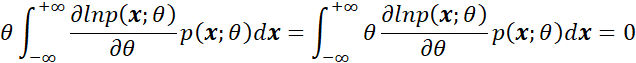
然后将两个式子相减，可以得到：
为了使用Cauchy-Schwarz不等式，将上式中的
拆成两个平方根相乘（概率密度非负，因此可以开根号），得到：
利用Cauchy-Schwarz不等式，可以得到：
而其中：
因此可以得到：
接下来证明：
还是从正则条件出发，存在：
两边对
求导，并进行积分求导操作互换，可以得到：
再次用到自然对数导数的性质，可以得到：
也即是：
因此，最终无偏估计量
方差的下限可以表示为：
CRLB下限证明完毕。
接下来讨论Cauchy-Schwarz不等式等式成立的条件：
在上面的计算过程中，用到了：
根据等式成立条件，那么假设存在一个与x无关的参数
，注意该参数与x无关，但可能与待估计的参数
有关，此时如果等式成立，那么存在：
把上式带入之后，即可得到：
为了求出此时的CRLB下限，将上式再对
求偏导，可以计算得到：
上式的化简，利用到了数学期望是对x求取，因此
和
对上述数学期望是常量。另外，由于
是无偏估计，因此：
最终可以得到：
因此，在Cauchy-Schwarz不等式等式成立的条件下，无偏估计期望的方差的下限满足：
上述
也被称为Fisher信息，显然
越大，估计方差的下限越小，那么越有可能得到该参数的有效估计。
接下来讨论如何利用CRLB推导中的结论，求方差达到CRLB的无偏估计：
如果对数概率密度对估计量的导数如果满足：
那么
就是方差达到CRLB的无偏估计，也称为有效估计量，此时估计量的方差达到CRLB下限：
注意：上述方法在实际工作中，只能用于一小部分有效估计方法求解，毕竟大部分场景下，无法表示成上述式子的形式。
最后，我们解决一开始提出的几个问题：
1. 如果仅用采集数据中的一个参数去估计A，那么：
对上述似然函数取对数，可以得到：
因此：
对比CRLB等号满足条件可以发现，此时：
因此，对观测数据，如果仅用一个数据去估计，那么不管从采集到的数据中去哪个元素作为估计量，该估计量都是有效估计，且此种情况下，方差的下限为
。
2. 如果用采集数据中的两个观测量去估计A，假设两个观测量属于独立同分布，那么联合概率密度：
其中i不等于j，因此似然函数的对数可以表示为：
可以进一步得到：
对比CRLB等号满足条件可以发现，此时：
因此，如果能取两个观测值进行估计，那么对两个观测值进行算数平均是参数A的有效估计，此时估计的CRLB方差的下限为
。
显然，前面工程问题中举例的
尽管是无偏估计，但不是有效估计，因为
的方差未能达到CRLB，而应该采用两个观测值的算数平均去估计参数A。
3. 如果用N个采集点都参与参数A的估计，且各个采集点都是独立同分布，那么似然函数可以表示为：
对上述取自然对数，可以得到：
对上述自然对数求偏导，可以得到：
通过对比，可以发现此时：
因此，对N个采集数据的算数平均是A的有效估计，其估计方差CRLB下限为
。
最终，根据一开始提出的工程问题，我们可以发现：
和
分别是采用一个观测数据和N个观测数据后对参数A的有效估计；- 对于独立同分布模型，采用N个观测数据的CRLB是采用单个观测数据CRLB的
。 - 对于类似具有高斯噪声的直流信号估计，如果单次能够采集到N个观测值，那么对N个观测值进行算术平均，得到的就是该直流信号的有效估计；且增加观测值的采样点数N，可以有效降低CRLB下限。
[1] 统计信号处理基础-估计与检测理论，50页,罗鹏飞译，2014.6