目录
1. 矢量形式的CRLB定理
如果要从采集到的一组观测量:
![]()
而其概率密度函数存在r个参数:
![]()
那么此时用来估计![]() 的似然函数可以表示为:
的似然函数可以表示为:
![]()
如果似然函数对每个参数都满足正则条件,即:
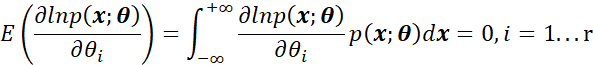
写成矩阵形式,即:
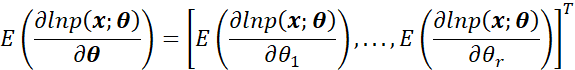
![]()
那么对每个无偏估计![]() 的方差,都存在一个下限,可以表示为:
的方差,都存在一个下限,可以表示为:
![]()
此下限被称为该无偏估计的CRLB下限,其中:![]() 为r*r维的Fisher信息矩阵,矩阵中每个元素定义为:
为r*r维的Fisher信息矩阵,矩阵中每个元素定义为:
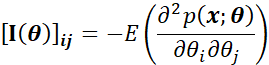
2. 矢量形式的CRLB定理详细证明过程
由于![]() 都是无偏估计,因此满足:
都是无偏估计,因此满足:
![]()
也就可以表示为:
![]()
用积分形式表示
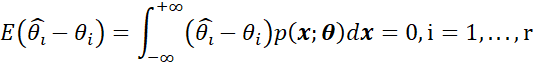
由于存在r个待估计参数,因此有r个无偏估计的积分形式。写成矩阵形式,可以表示为:
![]()
其中:
![]()
又由于存在r个待估计参数,因此![]() 对每个待估计参数进行偏导,即:
对每个待估计参数进行偏导,即:

除了当概率密度函数的非零域与未知参数有关之外,上述求导和积分可以互换[1]。或者可以描述为上述数学期望的上下限与估计量![]() 有关,那么求导与积分就不能互换。因此,我们对积分和求导交换顺序,得到:
有关,那么求导与积分就不能互换。因此,我们对积分和求导交换顺序,得到:
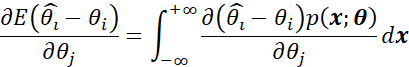


其中
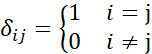
而显然又存在:

因此可以得到:
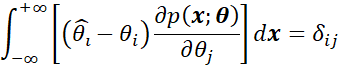
如果用对数函数求导性质,即:
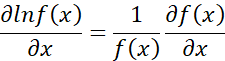
因此,可以得到:
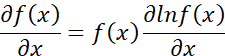
因此上式又可以转换为:
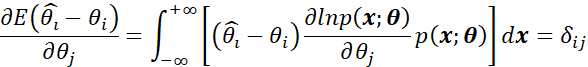
如果用矩阵形式表示:


而如果我们用:
![]()

那么进一步可以得到矢量形式的表达式,即:
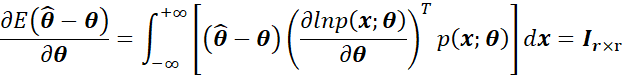
为了能够用Cauchy-Schwarz不等式,即:
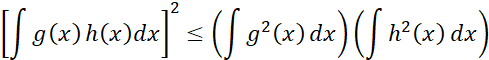
需要将r*r维矩阵,转换成为标量形式,那么我们可以将上述方阵,分别左乘和右乘一个任意数值的向量,得到:

其中:
![]()
![]()
注意,上述![]() 和
和![]() 可以是任意常数形式列向量,上述操作后,就将r*r维矩阵转换成单个元素,也就是:
可以是任意常数形式列向量,上述操作后,就将r*r维矩阵转换成单个元素,也就是:
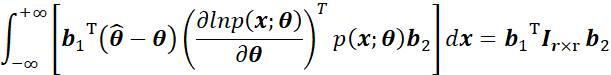
同样,由于概率密度的非负性, ![]() 是存在的,因此可以进一步转换为:
是存在的,因此可以进一步转换为:
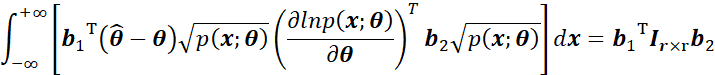
对应Cauchy-Schwarz不等式,如果我们令:
![]()
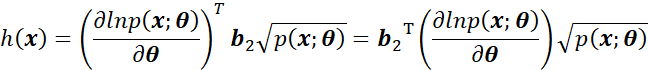
且,![]() 和
和![]() 都已经是标量形式,因此,使用Cauchy-Schwarz不等式结论后可以得到:
都已经是标量形式,因此,使用Cauchy-Schwarz不等式结论后可以得到:



又由于![]() 和
和![]() 是任意常数形式列向量
是任意常数形式列向量
因此,上式又可以转换为:
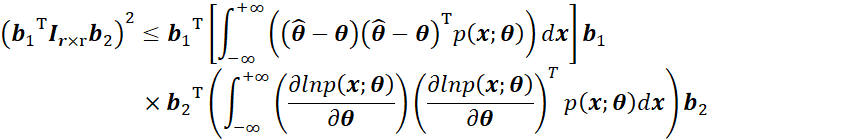
显然上述两个积分可以分别表示为:


其中
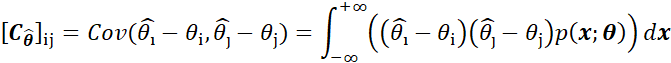
而

可以进一步证明(见下文第二部分证明):
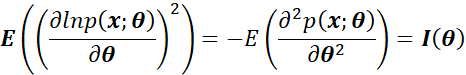
其中

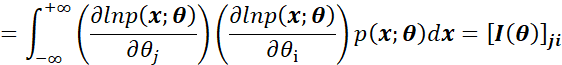
因此能得到:![]() ,
,![]()
因此,最终Cauchy-Schwarz不等式可以简化为:
![]()
由于![]() 和
和![]() 是任意的,因此可以假设他们之间存在如下关系:
是任意的,因此可以假设他们之间存在如下关系:
![]()
那么:
![]()
![]()
因此:
![]()
又由于正定矩阵性质,![]() 为大于0的标量元素,因此两边直接消除得到:
为大于0的标量元素,因此两边直接消除得到:
![]()
即:
![]()
而上式要对任意的向量![]() 都要成立,因此得到:
都要成立,因此得到:
![]()
上式表示左边的矩阵为非负定矩阵。而由于估计量![]() 的方差为
的方差为![]() 主对角线上元素,因此最终得到:
主对角线上元素,因此最终得到:
![]()
因此得到了矢量形式的CRLB。
当然如果r=1,那么直接可以得到:
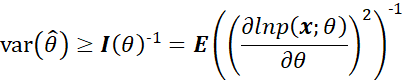
也就是标量形式的CRLB。
3. Fisher信息矩阵的两种等效形式证明
上述证明过程中,用到了:
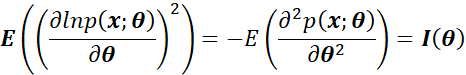
下面进行证明,利用正则条件,即:
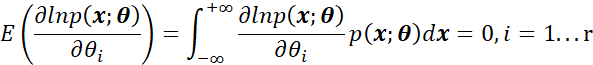
上式中对![]() 求偏导,得到:
求偏导,得到:
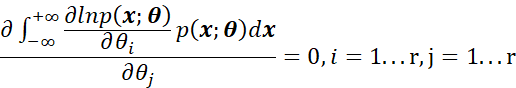
再次利用积分和偏导的可交换性,得到:

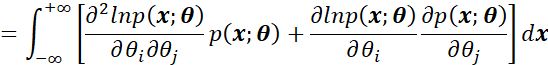
而又因为:
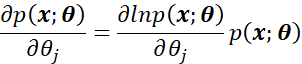
因此得到:

也就是:
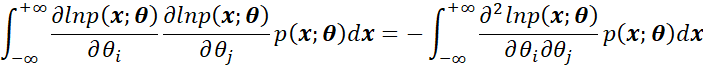
也就是

上式如果用矩阵形式表示,就是:
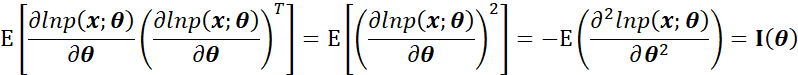
证明完毕。
4. Cauchy-Schwarz不等式中等式成立条件
根据Cauchy-Schwarz不等式性质,如果存在与x无关的常数,但该常数有可能是待估计量θ 的函数,因此用![]() 表示,满足:
表示,满足:
![]()
那么Cauchy-Schwarz不等式中的等式成立。
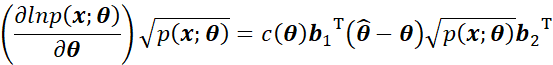
两边消除![]() 后,可以得到:
后,可以得到:

由于![]() 和
和![]() 是任意的,因此仍然可以假设他们之间存在如下关系:
是任意的,因此仍然可以假设他们之间存在如下关系:
![]()
同时考虑到![]() 是对称矩阵,那么得到:
是对称矩阵,那么得到:
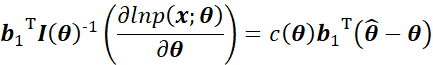
由于![]() 是任意的,因此存在:
是任意的,因此存在:
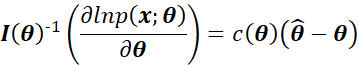
即需要满足:
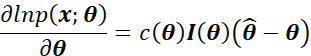
为了求出具体的![]() ,现对上式两边对
,现对上式两边对![]() 再次求偏导,得到:
再次求偏导,得到:
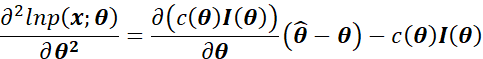
对等式两边求期望,得到:
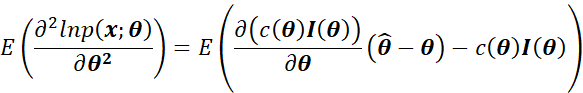
由于![]() 是无偏估计,且
是无偏估计,且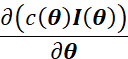 和
和![]() 均与观测量x无关,那么:
均与观测量x无关,那么:
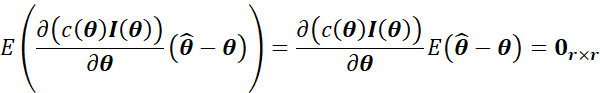
![]()
因此,最终得到:
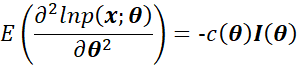
利用第二部分的证明,得到:
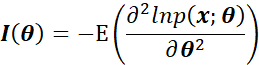
带入后得到:
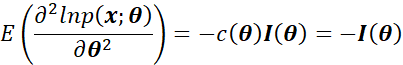
上式如果要成立,那么![]() 只能为1。
只能为1。
因此,最终Cauchy-Schwarz不等式中的等式成立的条件,也就是无偏估计方差能够达到CRLB下限的条件为:

也就是说,如果对似然函数的对数进行偏导后,能够写成上述形式,那么上式中的![]() 就是最小方差无偏估计,而估计的方差满足:
就是最小方差无偏估计,而估计的方差满足:
![]()
且达到CRLB下限。