python函数拟合

• 背景

最近在抖音直播数学答疑的时候，恰好有一位朋友问到了这个问题，已知x，z，y三列数据如上图所示，请问y的最后一位数是多少？

乍一看，还以为很简单，拎（抡）起粉笔就一顿操作（猛如虎）

（1）分别将x，z，y三列数据记作3个数列 { x n } , { z n } \{x_n\}, \{z_n\} { xn​},{ zn​} 和 { y n } \{y_n\} { yn​}， 其中n表示其所在数列的序号或位置。

（2）很容易发现如下规律
$$z_n-x_n=6\text{\hspace{1em}(1)}$$
和
$$x_n+y_n=x_{n+1}\text{\hspace{1em}(2)}$$
以及

$$z_n+y_n=z_{n+1}\text{\hspace{1em}(3)}$$

将（2）和（3）组合一下便得到（1），即

$$z_n-x_n=z_{n+1}-x_{n+1}=6\text{\hspace{1em}(4)}$$

而问题相当于是要求 { y n } \{y_n\} { yn​}的下一个$y_{n+1}$，上面3个关系式中却没有任何项涉及到，故这些关系不能解决根本问题，现在摆在我们面前的有两条路

• 找出数列 { x n } \{x_n\} { xn​} , { z n } \{z_n\} { zn​} 的下一项 m 和 m+6，然后利用（1）-（4）的关系进行求解$y_n$ 下一项 $\lambda$；

序号	1	2	3	4	5	6	7	8	9
x	-5	5	0	2	9	6	4	10	m
z	1	11	6	8	15	12	10	16	m+6
y	10	-5	2	7	-3	-2	6	$\lambda$

• 直接找出 { y n } 和 { x n } , { z n } \{y_n\} 和\{x_n\}, \{z_n\} { yn​}和{ xn​},{ zn​} 之间的关系表达式， 即

$$y_n=f(x_n,z_n)\text{\hspace{1em}(5)}$$

由 { x n } \{x_n\} { xn​} 和 { z n } \{z_n\} { zn​}的关系，（5）又可以改写成

$$y_n=f(x_n)\text{\hspace{1em}(6)}$$

第一条道路相当于绕了一圈，简称间接法，第二条道路更直接，简称直接法，我们先采用直接法来进行解答

• 先画出 { y n } 和 { x n } \{y_n\} 和\{x_n\} { yn​}和{ xn​}散点图

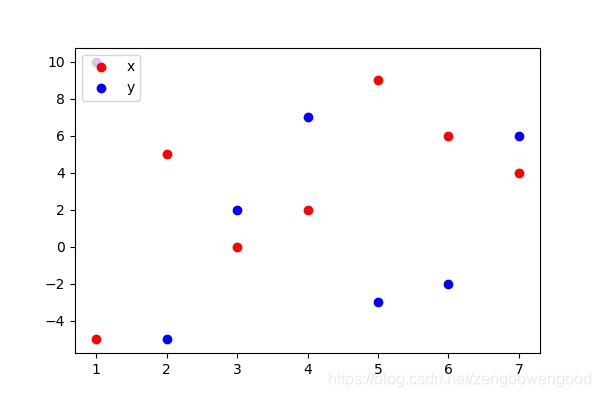
为了找出 { y n } 和 { x n } \{y_n\} 和\{x_n\} { yn​}和{ xn​}之间的函数关系，我们可以先建立一个最简单最纯粹的假设

$$y=ax+b\text{\hspace{1em}(7)}$$

没错，就是最简单的线性关系，然后拟合出来系数 a 和 b分别是 -0.97580645和5.0702765 （保留8位小数），这样 { y n } 和 { x n } \{y_n\} 和\{x_n\} { yn​}和{ xn​}之间的函数关系便是

$$y=-0.9758x+5.07\text{\hspace{1em}(8)}$$

然后画出来拟合函数，观察其与原数列之间的差距

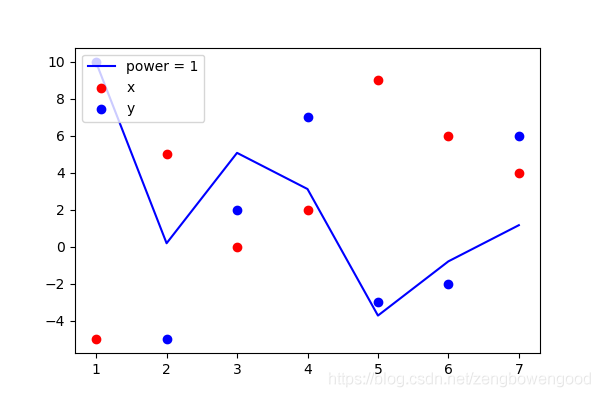
我们看到除了第1个点和第5个点靠得近，其余的点差距还是挺大的，既然一次拟合性能太差，那么我来个2次函数呗，即假设

$$y=a{x}^2+bx+c\text{\hspace{1em}(9)}$$

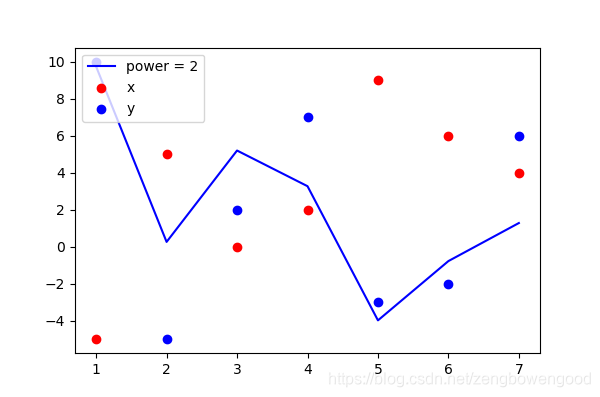
观察发现2次函数拟合和1次函数拟合没啥大的区别，再继续提高拟合函数次数

4次时候

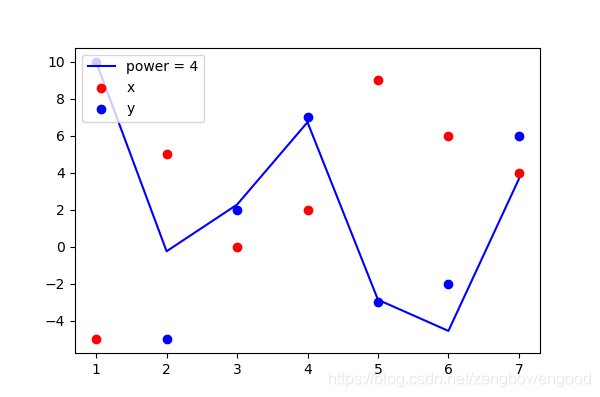
观察发现第1，3，4，5四个点都靠的比较近，差距在缩小，继续提高次数
5次的时候

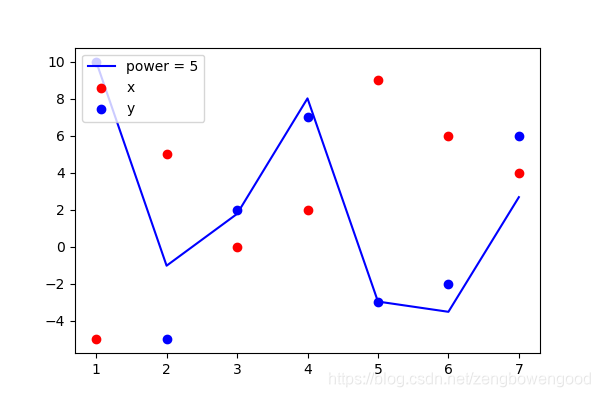
观察发现第2，6，7三个点拟合的还不够完美，继续提高次数

6次的时候

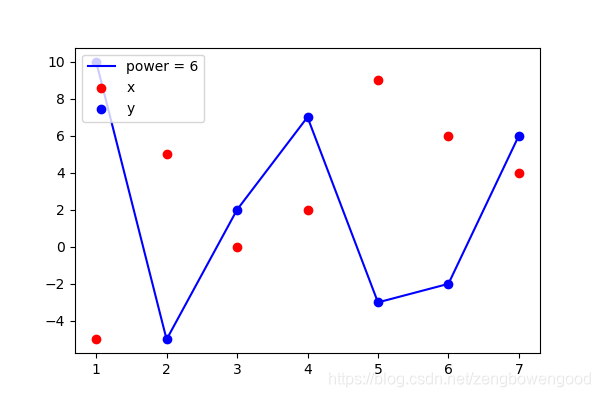
此时，拟合曲线恰好经过数列 { y n } \{y_n\} { yn​}的7点，可以认为拟合效果比较完美，此时的拟合函数为

$$y=-0.01265x^6+0.2035x^5-0.591x^4-4.176x^3+22.7x^2-24.32x+2\text{\hspace{1em}(10)}$$

将x = 10代入上（10）式，求得 y = -351.60606060605966
从y值可以猜出这是一个无限循环小数，循环节为6060，故最后所求的y值为

$$-351.\dot{6060}$$

• 完整代码

# -*- coding: utf-8 -*-
"""
Project name: 找规律
Description:
Created on Sun Sep 20 17:27:34 2020
@author: 帅帅de三叔    
"""
import numpy as np #导入数值分析模块
import matplotlib.pyplot as plt #导入绘图模块

x0 = [1, 2, 3, 4, 5, 6, 7]
x = [-5, 5, 0, 2, 9, 6, 4]
z = [1, 11, 6, 8, 15, 12, 10]
y = [10, -5, 2, 7, -3, -2, 6]

plt.figure(figsize = (6,4))
plt.scatter(x0, x, color = 'r', label = "x")
plt.scatter(x0, z, color = 'g', label = "z")
plt.scatter(x0, y, color ="brown", label = "y")

coef = np.polyfit(x, y, 6) #求出系数
print('拟合函数的系数 :\n', coef ) #打印出系数
funExpression = np.poly1d(coef) #求出表达式
print('拟合表达式 :\n',funExpression)  #打印出表达式
yFit =np.polyval(funExpression, x) #求出拟合函数的y值
print("拟合出来的y值：\n", yFit)
plt.plot(x0, yFit, color = 'blue', label ="fitting line")

nextY = np.polyval(funExpression, 10) #求出拟合函数的y值
print("所求的y的值为：", nextY )
plt.legend(loc = "upper left")
plt.show()

参考文献
1， https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.polyfit.html