关注公号【逆向通信猿】更精彩!!!
关于均衡的基础知识,首先可参考本人博客
LMMSE、Godard、CMA常模、Sato等算法在信道均衡中的应用理论与MATLAB仿真
理论推导
代价函数
J = E [ e G o d a r d p ( k ) ] = E [ ( ∣ y ( k ) ∣ q − r q ) p ] = E [ ( ∣ w H ( k ) x ( k ) ∣ q − r q ) p ] J = E\left[ {e_{Godard}^p(k)} \right] = E\left[ { { {\left( { { {\left| {y(k)} \right|}^q} - {r_q}} \right)}^p}} \right] = E\left[ { { {\left( { { {\left| { {\boldsymbol{w}^H}(k)\boldsymbol{x}(k)} \right|}^q} - {r_q}} \right)}^p}} \right] J=E[eGodardp(k)]=E[(∣y(k)∣q−rq)p]=E[(∣∣wH(k)x(k)∣∣q−rq)p]
其中, r q = E [ ∣ x ( k ) ∣ 2 q ] E [ ∣ x ( k ) ∣ q ] {r_q} = \frac{ {E\left[ { { {\left| {\boldsymbol{x}(k)} \right|}^{2q}}} \right]}}{ {E\left[ { { {\left| {\boldsymbol{x}(k)} \right|}^q}} \right]}} rq=E[∣x(k)∣q]E[∣x(k)∣2q],p和q是正整数。
求梯度
用瞬时误差代替平均误差,求瞬时误差对于 w ∗ \boldsymbol w^* w∗的梯度,也就是代价函数变化率最大的方向,注意是 w ∗ \boldsymbol w^* w∗而不是 w \boldsymbol w w
∇ w ∗ J = p e G o d a r d p − 1 ( k ) ∂ ( ∣ y ( k ) ∣ q ) ∂ w ∗ ( k ) = 1 2 p q e G o d a r d p − 1 ( k ) ∣ y ( k ) ∣ q − 2 ∂ ( ∣ y ( k ) ∣ 2 ) ∂ w ∗ ( k ) = 1 2 p q e G o d a r d p − 1 ( k ) ∣ y ( k ) ∣ q − 2 ∂ ( w H ( k ) x ( k ) x H ( k ) w ( k ) ) ∂ w ∗ ( k ) = 1 2 p q e G o d a r d p − 1 ( k ) ∣ y ( k ) ∣ q − 2 x ( k ) x H ( k ) w ( k ) = 1 2 p q e G o d a r d p − 1 ( k ) ∣ y ( k ) ∣ q − 2 y ∗ ( k ) x ( k ) \begin{array}{l} {\nabla _{
{\boldsymbol{w}^*}}}J = pe_{Godard}^{p - 1}(k)\frac{
{\partial ({
{\left| {y(k)} \right|}^q})}}{
{\partial {\boldsymbol{w}^*}(k)}}\\ = \frac{1}{2}pqe_{Godard}^{p - 1}(k){\left| {y(k)} \right|^{q - 2}}\frac{
{\partial ({
{\left| {y(k)} \right|}^2})}}{
{\partial {\boldsymbol{w}^*}(k)}}\\ = \frac{1}{2}pqe_{Godard}^{p - 1}(k){\left| {y(k)} \right|^{q - 2}}\frac{
{\partial ({\boldsymbol{w}^H}(k)\boldsymbol{x}(k){\boldsymbol{x}^H}(k)\boldsymbol{w}(k))}}{
{\partial {\boldsymbol{w}^*}(k)}}\\ = \frac{1}{2}pqe_{Godard}^{p - 1}(k){\left| {y(k)} \right|^{q - 2}}\boldsymbol{x}(k){\boldsymbol{x}^H}(k)\boldsymbol{w}(k)\\ = \frac{1}{2}pqe_{Godard}^{p - 1}(k){\left| {y(k)} \right|^{q - 2}}{y^*}(k)\boldsymbol{x}(k) \end{array} ∇w∗J=peGodardp−1(k)∂w∗(k)∂(∣y(k)∣q)=21pqeGodardp−1(k)∣y(k)∣q−2∂w∗(k)∂(∣y(k)∣2)=21pqeGodardp−1(k)∣y(k)∣q−2∂w∗(k)∂(wH(k)x(k)xH(k)w(k))=21pqeGodardp−1(k)∣y(k)∣q−2x(k)xH(k)w(k)=21pqeGodardp−1(k)∣y(k)∣q−2y∗(k)x(k)
其中,涉及相关的矩阵运算的公式为
y ( k ) = w H ( k ) x ( k ) y ∗ ( k ) = w T ( k ) x ∗ ( k ) = x H ( k ) w ( k ) ∇ z ∗ ( Z H R Z ) = R Z \begin{array}{l} y(k) = {\boldsymbol{w}^H}(k)\boldsymbol{x}(k)\\ {y^*}(k) = {\boldsymbol{w}^T}(k){\boldsymbol{x}^*}(k) = {\boldsymbol{x}^H}(k)\boldsymbol{w}(k)\\ {\nabla _{
{\boldsymbol{z}^*}}}({\boldsymbol{Z}^H}\boldsymbol{R}\boldsymbol{Z}) = \boldsymbol{R}\boldsymbol{Z} \end{array} y(k)=wH(k)x(k)y∗(k)=wT(k)x∗(k)=xH(k)w(k)∇z∗(ZHRZ)=RZ
得到更新方程为
w ( k + 1 ) = w ( k ) − 1 2 μ p q ( ∣ y ( k ) ∣ q − r q ) p − 1 ∣ y ( k ) ∣ q − 2 y ∗ ( k ) x ( k ) \boldsymbol{w}(k + 1) =\boldsymbol{w}(k) - \frac{1}{2}\mu pq{\left( {
{
{\left| {y(k)} \right|}^q} - {r_q}} \right)^{p - 1}}{\left| {y(k)} \right|^{q - 2}}{y^*}(k)\boldsymbol{x}(k) w(k+1)=w(k)−21μpq(∣y(k)∣q−rq)p−1∣y(k)∣q−2y∗(k)x(k)
当p=q=2时,即为常模(CMA)算法,更新公式可以写成
w ( k + 1 ) = w ( k ) − 2 μ e C M A ∗ ( k ) x ( k ) \boldsymbol{w}(k + 1) = \boldsymbol{w}(k) - 2\mu e_{CMA}^*(k)\boldsymbol{x}(k) w(k+1)=w(k)−2μeCMA∗(k)x(k)
其中, e C M A ( k ) = y ( k ) ( ∣ y ( k ) ∣ 2 − r q ) e_{CMA}(k)=y(k)\left( { { {\left| {y(k)} \right|}^2} - {r_q}} \right) eCMA(k)=y(k)(∣y(k)∣2−rq)
MATLAB仿真
代码
进行20次蒙特卡洛仿真取平均值,用剩余码间干扰来衡量盲均衡性能曲线,采用CPU并行计算,加快计算速度。
clc;clear;close all;
len = 5000;
SNR = 30;
h = [0.26, 0.93, 0.26].'; % 信道
h = h/norm(h);
N = 11;M = 4; iniphase = 0;
mu = 0.01; R=1; times=10;
ISI_CMA=zeros(times,len); yout=zeros(times,len);
parfor nt=1:times
x = randi([0,M-1],len,1);
s = pskmod(x,M,iniphase);
r = conv(s,h,'same');
rn = awgn(r,SNR,'measured');
w = zeros(N,len); w(ceil(N/2),N) = 1;
y=zeros(1,len); err=zeros(1,len); ISI = zeros(1,len);
for n = N:len
yk=rn(n:-1:n-N+1);
y(n)=w(:,n)'*yk;
err(n) = y(n)*(abs(y(n)).^2-R);
w(:,n+1) = w(:,n)-mu*conj(err(n))*yk;
sita = conv(w(:,n+1),h);
ISI(n-N+1) = sum(abs(sita).^2)/max(abs(sita))^2-1;
end
ISI_CMA(nt,:)=ISI;
yout(nt,:)=y;
end
tx = 1:len-N+1;
maker_idx = 1:300:length(tx);
figure;plot(tx,mean(10*log10(ISI_CMA(:,tx)),1),'o-b','MarkerIndices',maker_idx,'LineWidth',1.2);
xlabel('Iterations','FontSize',14);ylabel('ISI (dB)','FontSize',14);
legend('CMA','FontSize',14);
set(gca,'FontSize',16,'Fontname', 'Times New Roman');
结果
当 μ = 0.01 \mu=0.01 μ=0.01时,ISI曲线如下
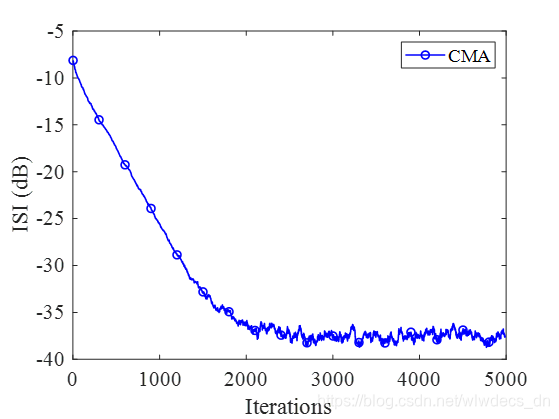
星座图如下
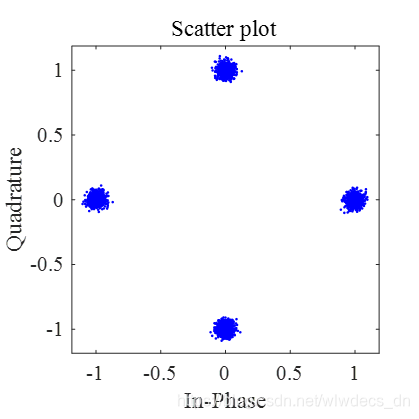
当 μ = 0.05 \mu=0.05 μ=0.05时,ISI曲线如下
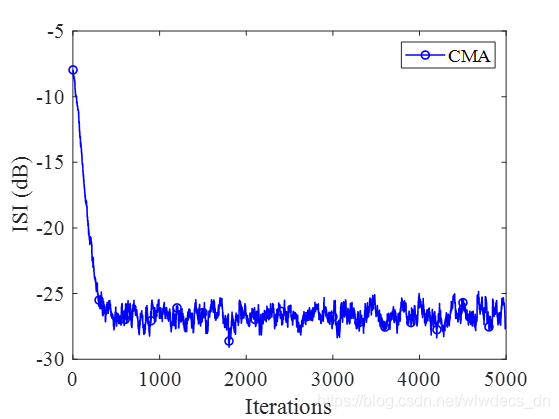
星座图如下
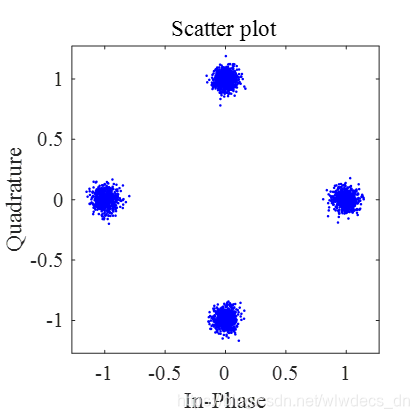
可以看到,随着迭代步长 μ \mu μ的增大,收敛速度增大的同时稳态误差有所减小。