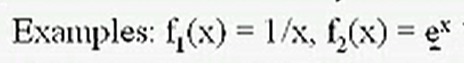【最优化】最优化的相关条件

最优化的相关条件

---

一. 局部极值点的必要条件

既然在前一节中我们对于局部(全局)极值点进行了讨论，那么我们也想要知道，如果一个点是极值点，那么它需要满足什么条件？

1. 局部极小点的必要条件

若点x₀是函数f(x)的局部极小值点，则有：

• x₀是f(x)的驻点——(f(x)在x₀处的一阶导数为0)
• f(x)在x₀处的Hessian矩阵H(x₀)是半正定的

2. 证明

【自我小结】

• 有关极值的相关证明经常用到极值的定义和泰勒展开
• 反证法也是经常用到的证明思路
• 为了构造出上面所需的定义和泰勒展开式，往往会取某个点的邻域进行相应的演算。

3. 局部极大点的必要条件

前面虽然都是在以局部极小点为例进行探讨，但是我们可以很容易地将结论迁移类比到局部极大值上面。

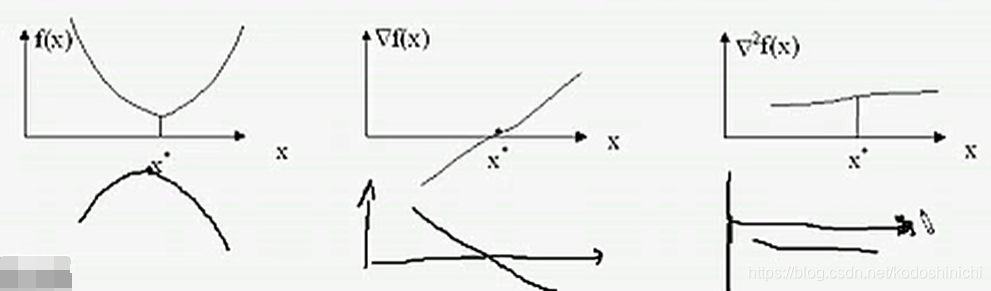
根据上图我们可知，如果一个点x₀是f(x)的局部极大值点，则有：

• f(x)在x₀处的一阶导数值为0
• f(x)在x₀的Hessian矩阵是负半定的

---

二. 局部极值点的充分条件

1. 局部极小值的充分条件

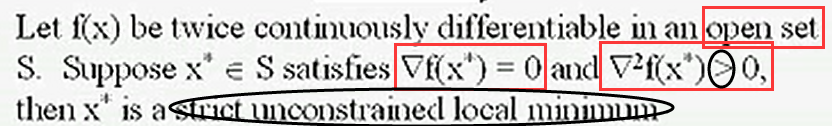
若函数f(x)上的某一点x₀满足：

• x₀是f(x)的驻点——(f(x)在x₀处的一阶导数为0)
• f(x)在x₀处的Hessian矩阵H(x₀)是正定的

则可得到，x₀就是f(x)的严格的局部极小值点(<)

2. 证明

3. 注意事项

①对照充分条件和必要条件，可知充分条件比必要条件更加严苛(必要条件涵盖了充分条件)
②充分条件的适用范围更窄，函数需要定义在开集上，且函数需要二阶可微

在实际问题中，函数往往是定义在闭集上，而且最优点很可能就出现在端点上。

这个时候，我们可以先利用充分条件找到该闭集对应的开集中的最优点，再和端点上的函数值进行比较，从而确定整个闭集上的最优点。

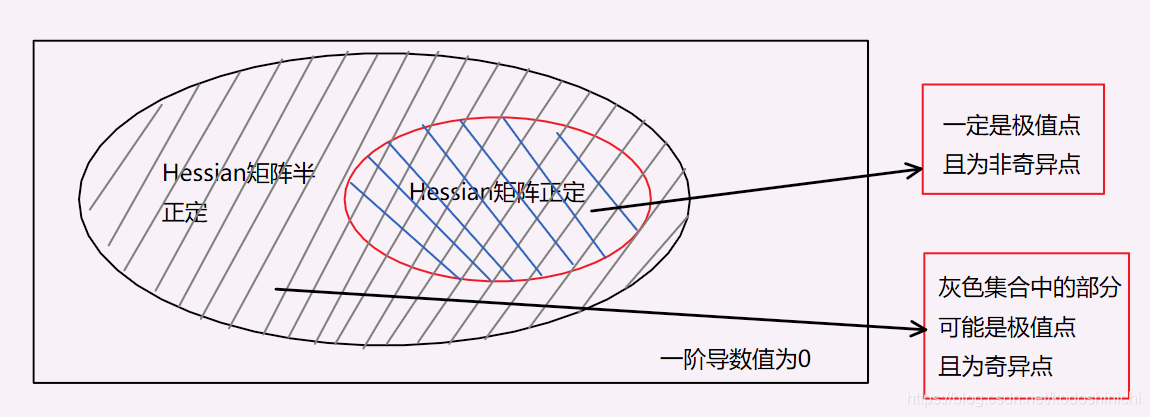
③用充分条件可以直接找到极值点中的所有非奇异点，奇异点则较难寻找

注意分辨“充分条件和“必要条件”的关系

• 满足了充分条件的点一定是非奇异极值点，不满足充分条件的点不一定不是极值点
• 所有极值点都必须满足必要条件，满足了必要条件不一定就是极值点
• 满足了必要条件，但不满足充分条件的那些极值点就称为奇异点

④对于一个定义在开集X上的可微凸函数f(x)而言，▽f(x^*) = 0↔点x^*是f(x)的全局极小值点。

【简要证明】
根据上一篇博文《【最优化】最优化理论的基本概念》中的《可微函数的凸性三定理》的定理一：

我们可以任取一个x∈X，则有f(x)-f(x^*)≥▽f(x^*)^T·(x-x^*)；
又因为根据题意，▽f(x^*)^T = 0，所以可得f(x)-f(x^*)≥0

从而证得x^*就是f(x)的全局极小值点。

---

【例】求解给定函数的局部极值点

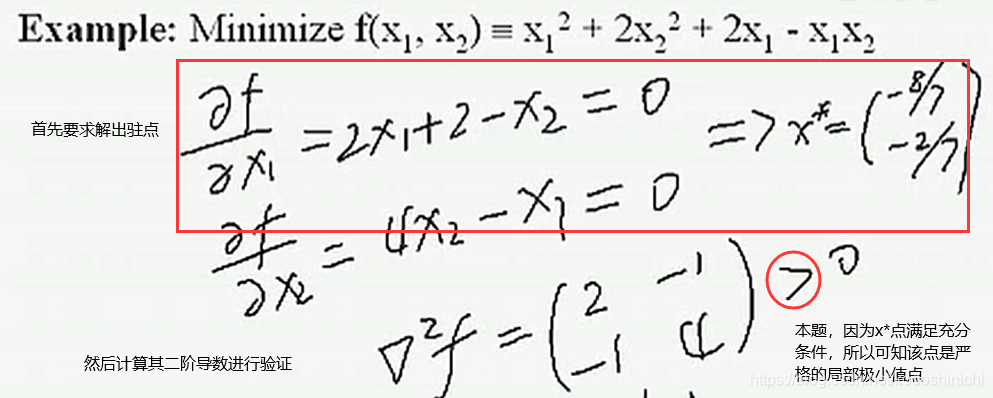
关于极值点求解的题型要注意：

• 求解出驻点之后，一定要用二阶导进行验证，才能明确是不是极小(大)值点
• 只能得出该点满足必要条件，则不能下结论说该点是局部极值点
• 不同函数在某点的一阶导和二阶导处具有相同的性质，这并不意味着该点在两个函数中是相同性质的点，可以通过计算更高阶导数进行分析

---

三. 局部极值点的存在条件

不是所有的函数都存在极值点：

1. 极值点的存在条件

总的来说，我们只需要记住在一个给定的有界区间内求解，一般都是有极值点的

2. 讨论极值点的各类条件的原因

本节我们讨论了极值点的充分、必要、充分必要及存在性条件。

• 帮助理解极值求解过程
• 当条件满足时，我们可以适时地终止一个迭代算法
• 可以帮助优化算法