流体扰动原理的动、静态避障三维轨迹规划算法实现

思想

在一条河边仔细观察会发现水流流过河中凸起的石头时会从石头旁边平滑地流过，这是流场的作用。受此启发，将这一思想拓展到UAV或者是任何背景的三维或者是二维轨迹规划问题，即可得到本文所讲述的流体扰动原理规划算法。

这一算法实际上属于人工势场算法的一种变形，在没有障碍物的前提下，三维空间中存在一个初始的流场，这个流场指向目标点，使轨迹向目标点汇流。当空间中存在障碍物时，障碍物产生一个扰动流场，扰动流场与初始流场同时作用形成合成流场，合成流场的流线即为规划轨迹。可以将扰动流场算法中的初始流场看做人工势场算法中的引力场，扰动场看做斥力场，两者异曲同工。

初始流场的建立

以汇流作为初始流场，其流速$u(\mathbf{P})$定义为：
$$\mathbf{u}(\mathbf{P})=-{\left[\frac{C\left(x-x_{\mathrm{d}}\right)}{d\left(\mathbf{P},{\mathbf{P}}_{\mathrm{d}}\right)},\frac{C\left(y-y_{\mathrm{d}}\right)}{d\left(\mathbf{P},{\mathbf{P}}_{\mathrm{d}}\right)},\frac{C\left(z-z_{\mathrm{d}}\right)}{d\left(\mathbf{P},{\mathbf{P}}_{\mathrm{d}}\right)}\right]}^{\mathrm{T}}$$
其中$C$为汇流速度，$d$为无人机位置$\mathbf{P}$与目标位置${\mathbf{P}}_{\mathbf{d}}$的距离：
$$d\left(\mathbf{P},{\mathbf{P}}_{\mathrm{d}}\right)=\sqrt{{{\left(x-x_{\mathrm{d}}\right)}^2+g(y)-y_{\mathrm{d}})}^2+{\left(z-z_{\mathrm{d}}\right)}^2}$$

初始流场示意图如下（红色曲线为流场线）：

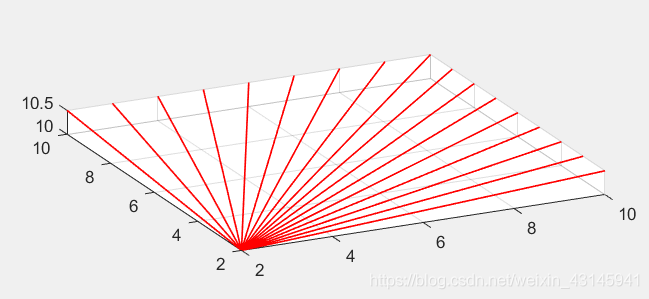
扰动流场的建立

障碍物方程

假设1：运动目标假定为质点，所有障碍物和威胁等均用圆球、圆锥、圆柱、长方体等标准的凸多面体等效：
$$\Gamma (\mathbf{P})={\left(\frac{x-x_0}{a}\right)}^{2p}+{\left(\frac{y-y_0}{b}\right)}^{2q}+{\left(\frac{z-z_0}{c}\right)}^{2r}$$
式中：常数$a、b、c$和$p、q、r$分别决定凸面体的大小与形状，$(x_0,y_0,z_0)$表示凸面体的中心，$\Gamma (\mathbf{P})=1$即为障碍物表面方程。

扰动流场

假设环境中有$W$个障碍物，将障碍物对初始流场的扰动用扰动矩阵$\overline{\mathbf{M}}(\mathbf{P})$量化表示：
$$\overline{\mathbf{M}}(\mathbf{P})=\prod _{w=1}^W{\mathbf{M}}_{\mathbf{\omega }}(\mathbf{P})$$
式中：$\overline{\mathbf{M}}(\mathbf{P})$为第$\omega$个障碍物的扰动矩阵：
$$M_w(P)=I-\frac{{\omega }_w(\mathbf{P}){\mathbf{n}}_w(\mathbf{P}){\left({\mathbf{n}}_w(\mathbf{P})\right)}^{\mathrm{T}}}{{\left|\Gamma (\mathbf{P}))\right|}^{\frac{1}{{\rho }_w}}{\left({\mathbf{n}}_w(\mathbf{P})\right)}^{\mathrm{T}}{\mathbf{n}}_w(\mathbf{P})}$$
式中：$I$为单位矩阵；${\rho }_w$为第$w$个障碍物的反应系数，而${\omega }_w(\mathbf{P}),{\mathbf{n}}_w(\mathbf{P})$按如下公式计算：
$$\begin{array}{cc}{\omega }_w(P)=& \\ 1& W=1\\ {\prod }_{i=1}^W\frac{{\Gamma }_i(P)-1}{\left({\Gamma }_i(P)-1\right)+\left({\Gamma }_w(P)-1\right)}& W\ne 1\end{array}$$
$${\mathbf{n}}_w(\mathbf{P})={\left[\frac{\delta {\Gamma }_w(\mathbf{P})}{\delta x}\frac{\delta {\Gamma }_w(\mathbf{P})}{\delta y}\frac{\delta {\Gamma }_w(\mathbf{P})}{\delta z}\right]}^{\mathrm{T}}$$
至此，我们可以计算出扰动矩阵$\overline{\mathbf{M}}(\mathbf{P})$，利用它修正初始流场流速，得到合成流场：
$$\overline{\mathbf{u}}(\mathbf{P})=\overline{\mathbf{M}}(\mathbf{P})\mathbf{u}(\mathbf{P})$$
通过积分$\overline{\mathbf{u}}(\mathbf{P})$，可以获得轨迹下一点位：
$${\mathbf{P}}_{\text{next }}=\mathbf{P}+\overline{\mathbf{u}}(\mathbf{P})\Delta t$$
式中：$\Delta t$为计算步长，如此迭代求解得到一系列离散点，将其连线即形成扰动流线，即规划路线。

仿真结果

目标点：$goal=[2,2,10];$
参数：$C=1;row=1.2;$
障碍物坐标以及半径：
$$\begin{gathered} obstacleMatrix=[4,6,10;6,4,10;8,8,10]; \\ obstacleRMatrix=[1,1,1.2]; \end{gathered}$$

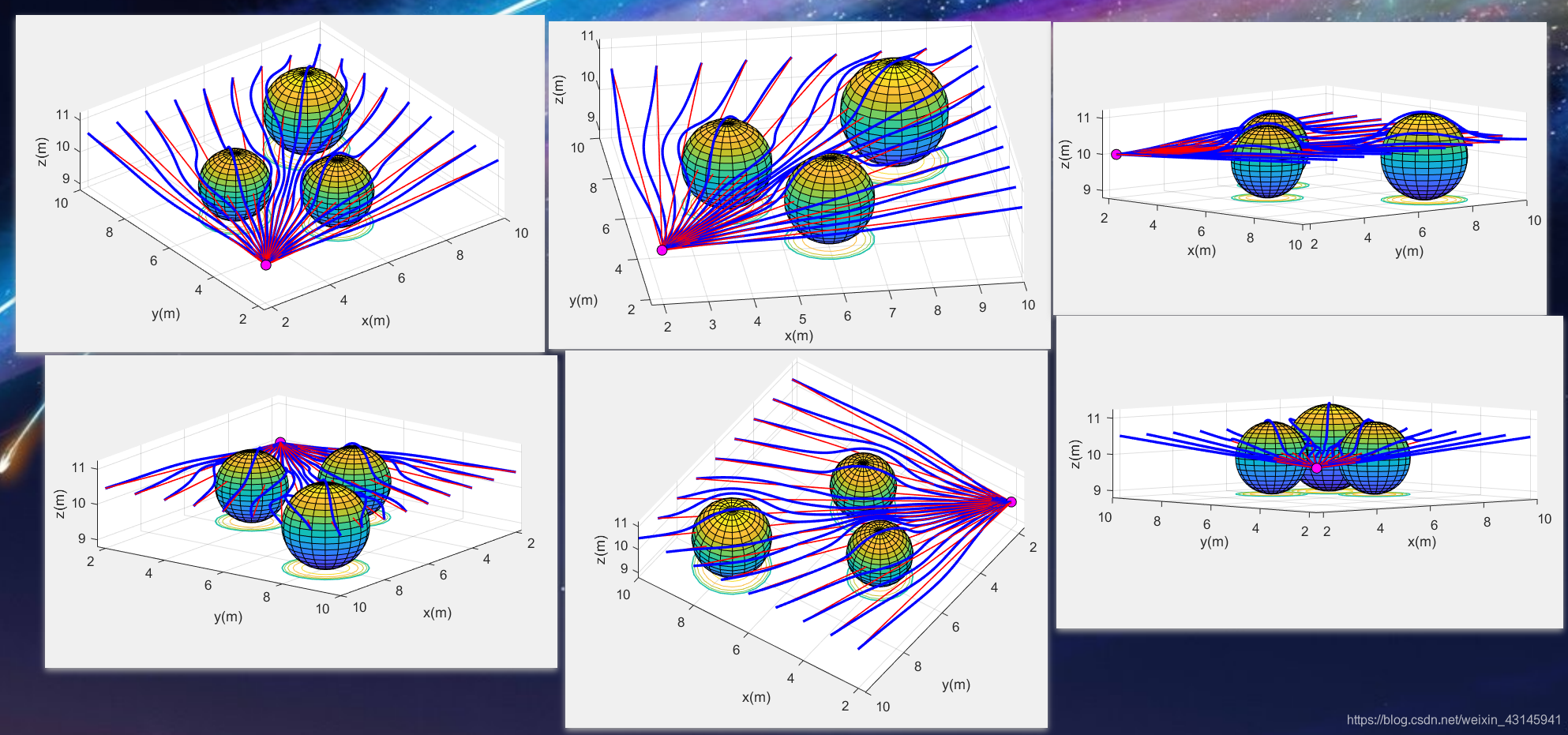
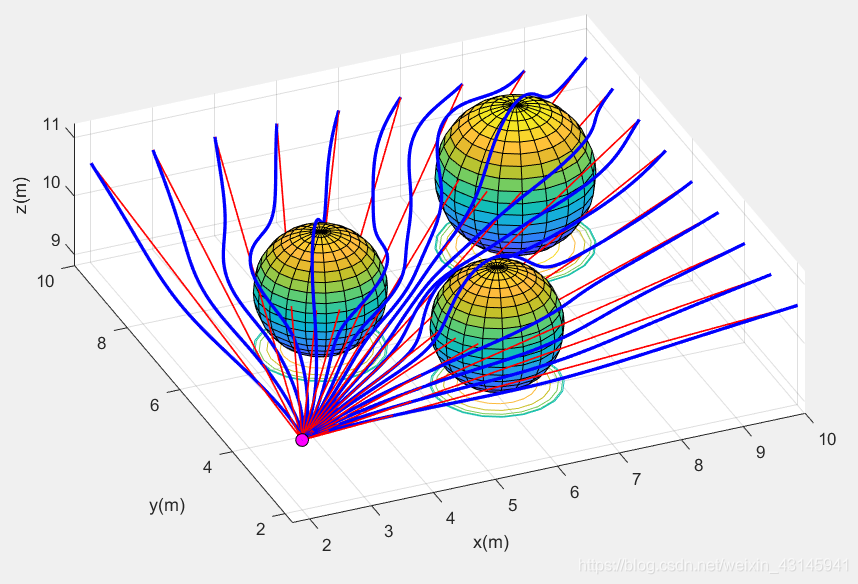
其中红线为初始流场线，蓝色为合成流场线（规划路线）,可以看到规划路线平滑地绕开球形障碍物到达目标点（理论上在没有其他约束的情况下不会与障碍物有相交的情况），在众多规划算法中可以说达到SOTA效果。

动态障碍

动态障碍轨迹规划的实现需要考虑障碍的速度，其基本思想就是在某一时刻按照静态流场计算出下一点位（相对位置）后加上障碍物的速度乘以时间步长（绝对位置）。
$$\begin{gathered} \bar{u}(P)=\bar{M}(P)(u(P)-v(P))+v(P) \\ {\mathbf{P}}_{\mathrm{n}\mathrm{e}\mathrm{x}\mathrm{t}}=\mathbf{P}+\overline{\mathbf{u}}(\mathbf{P})\Delta t \end{gathered}$$
而$v(P)$是真实障碍物速度${\mathbf{v}}_w(\mathbf{P}))$的加权，让轨迹靠近障碍物时更多地考虑障碍物的速度，而原理障碍物时不太考虑障碍物的速度：
$$\mathbf{v}(\mathbf{P})=\sum _{w=1}^W{\omega }_w(\mathbf{P}){\mathrm{e}}^{\frac{-{\Gamma }_w(P)}{\lambda }}{\mathbf{v}}_w(\mathbf{P})$$

另外，流体法还可以应用于目标点也在运动的情况，这时初始流场需要考虑目标点的运动速度：
$$\begin{array}{c}\mathbf{u}(\mathbf{P})=k_1{\mathbf{u}}_1(\mathbf{P})+k_2{\mathbf{u}}_2(\mathbf{P})\\ k_1={\left(\frac{d\left(\mathbf{P}{\mathbf{P}}_{\mathrm{d}}\right)}{d\left({\mathbf{P}}_0{\mathbf{P}}_{\mathrm{d}0}\right)}\right)}^m\\ k_2=1-k_1\end{array}$$
Pd是目标点坐标，P是当前轨迹坐标，P0是初始点坐标。

动态障碍规划效果：


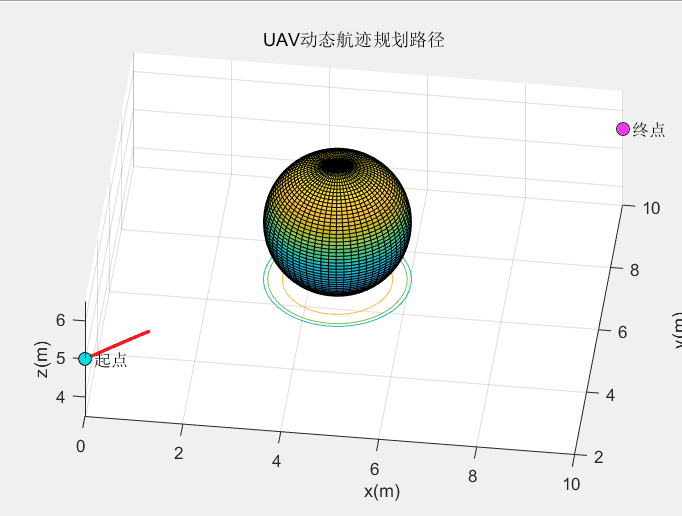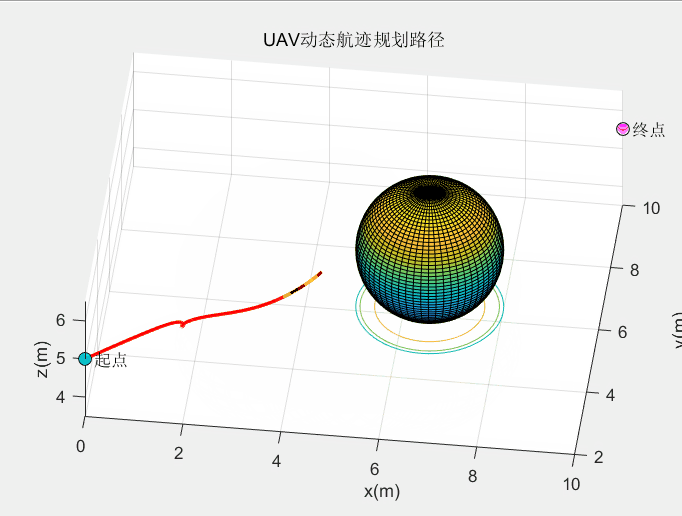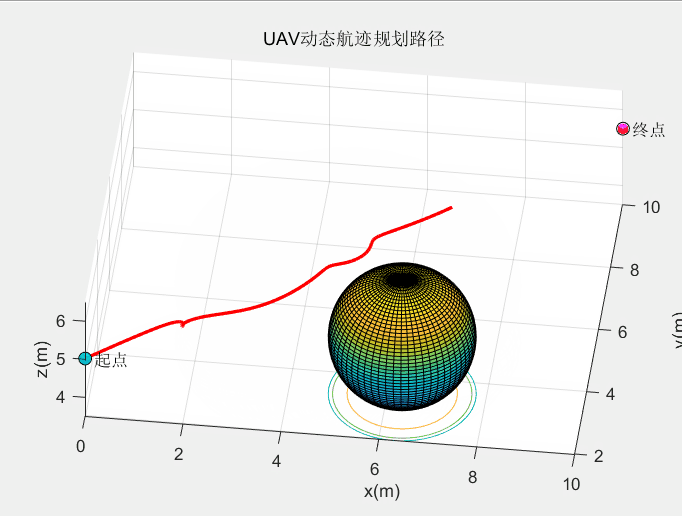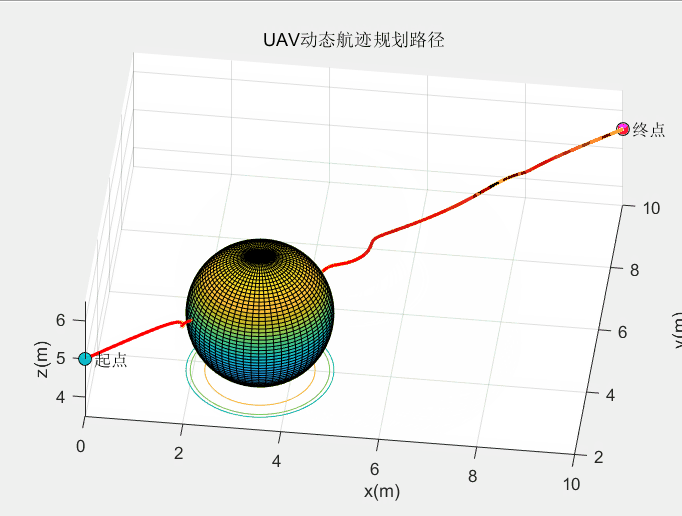
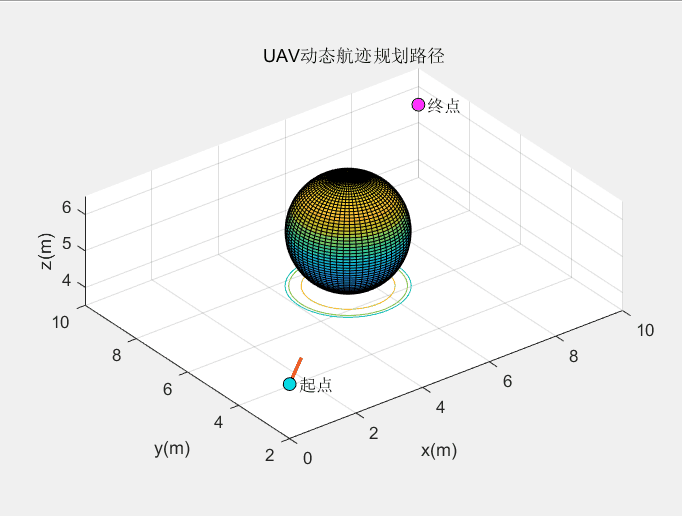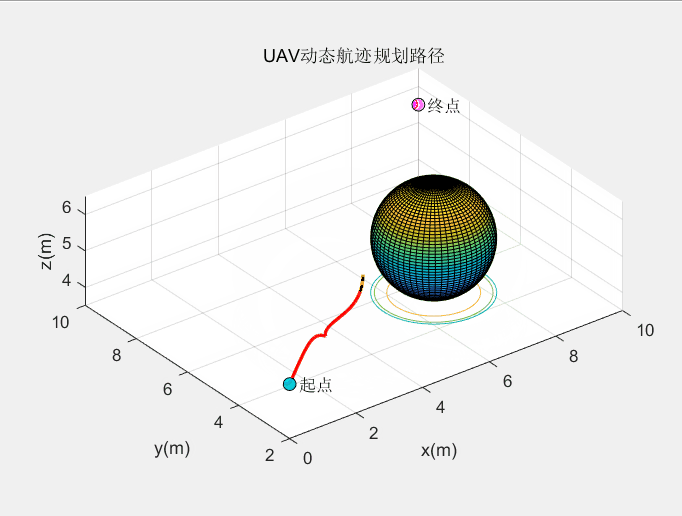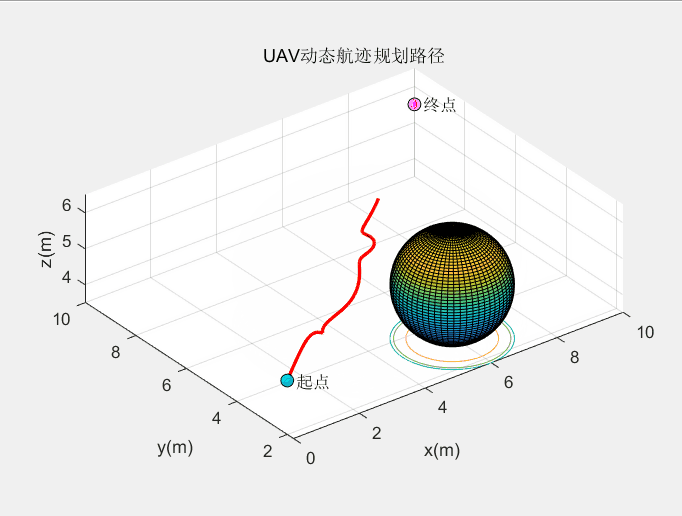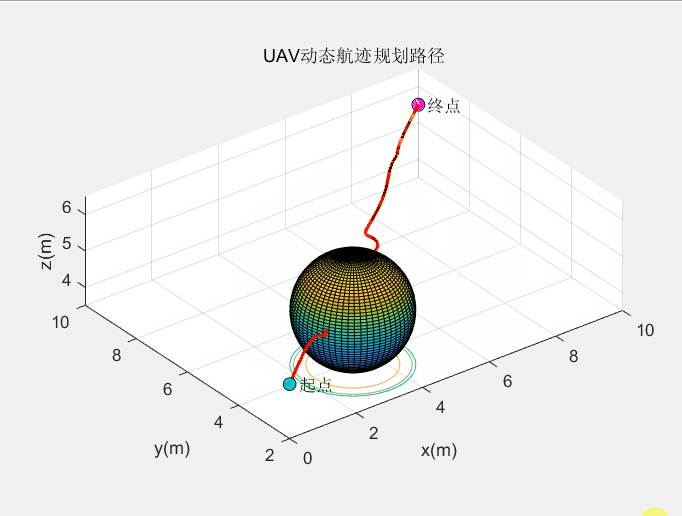
这个算法的动态避障效果较绝大多数算法都要好。

一种更优秀的改良算法

IIFDS

缺点

对于形状复杂的障碍物由于其$\Gamma (\mathbf{P})$复杂甚至不能用$\Gamma (\mathbf{P})$的形式表示，因此在含有这种障碍物的环境下使用流场法会出现一定的困难，而人工势场法则没有这种问题。另外，当起始点、障碍物中心点、目标点在共线时会出现无解现象，但是这种情况发生条件较为苛刻，可以忽略。

参考文章

[1]. 王宏伦, 姚鹏, 梁宵, 等.基于流水避石原理的无人机三维航路规划[J].电光与控制, 2015, 22(10):1-6.