分治策略中,我们递归地求解一个问题,每层递归中应用如下三个步骤:
1.分解。将问题划分为一些子问题,子问题的形式与原问题一样,只是规模更小。
2.解决。递归地求解出子问题,如果子问题规模足够小,则停止递归,直接求解。
3.合并。将子问题的解组合成原问题的解。
当子问题足够大,需要递归求解时,我们称之为递归情况。当子问题变得足够小,不再需要递归时,我们说递归已经触底,进入了基本情况。
递归式可以有很多形式,一个递归算法可将问题划分为规模不等的子问题,如1/3和2/3的划分。且子问题的规模不必是原问题规模的一个固定比例。
实际应用中,我们会忽略递归式声明和求解的一些技术细节,如对n个元素调用MERGE-SORT,当n为奇数时,两个子问题的规模分别为n/2向上取整和向下取整,而非准确的n/2。边界条件是另一类通常忽略的细节,当n足够小时,算法运行时间为θ(1),但我们不改变求T(n)时n足够小时的递归式,因为这些改变幅度不会超过一个常数因子,因而函数的增长阶不会变化。
投资股票问题,只能买卖一次,希望最大化收益,即最低价买入,最高价卖出,但可能最低价出现在最高价之后:

你可能认为可以在价格最低时买进,或价格最高时卖出,即可最大化收益,如果这种策略有效,则确定最大化收益是非常简单的:寻找最高价格和最低价格,然后从最高价格开始向左寻找左边的最低价格,从最低价格开始向右寻找右边的最高价格,然后取两对价格中差值最大者,但下图是反例:
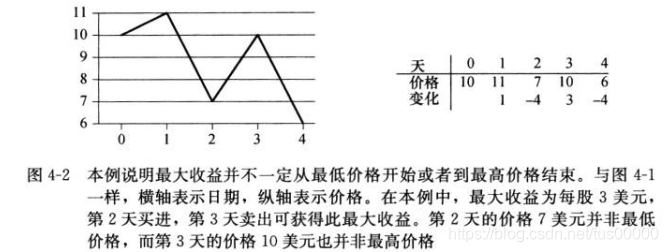
以上问题可以简单地暴力求解,尝试每对可能的买进和卖出日期组合,只要卖出日期在买入日期之后即可,n天中共有n(n-1)/2种日期组合,而处理每对日期所花费的时间至少也是常量,因此,这种方法运行时间为Ω(n²)。
我们可以考察每日价格变化,第i天的价格变化定义为第i天和第i-1天的价格差,那么问题也就变成了寻找和最大的非空连续子数组,称这样的子数组为最大子数组:
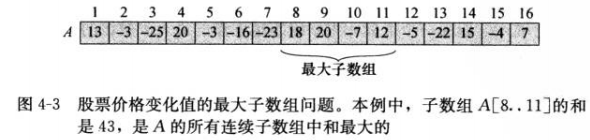
只有当数组中包含负数时,最大子数组问题才有意义,如果所有数组元素都是非负的,最大子数组就是整个数组中的和。
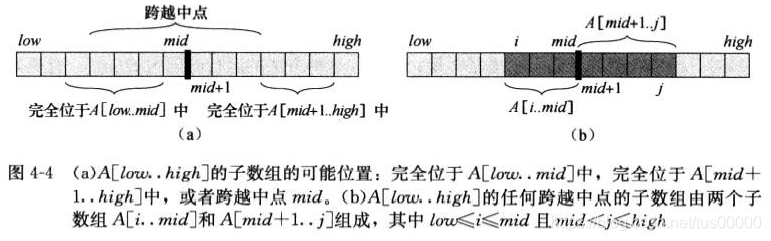
考虑用分治技术求解最大子数组问题,使用分治技术意味着我们要把子数组划分为两个规模尽量相等的子数组,即找到子数组的中央位置mid,然后考虑求解两个子数组A[low … mid]和A[mid + 1 … high],A[low … high]的任何连续子数组A[i … j]所处的位置必定是以下三种情况之一:
1.完全位于子数组A[low … mid]中,此时low <= i <= j <= mid。
2.完全位于子数组A[mid + 1 … high]中,此时mid < i <= j <= high。
3.跨越了中点,此时low <= i <= mid <= j <= high。
实际上,A[low … high]的一个最大子数组必然是完全位于A[low … mid]中、完全位于A[mid + 1 … high]、跨越中点的所有子数组中和最大者,我们可以递归地求解完全位于两边的最大子数组,因此剩下的全部工作就是寻找跨越中点的最大子数组,然后在这三种情况中选取和最大者:
求跨越中点的最大子数组:
FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)
left-sum = -∞
sum = 0
for i = mid down to low
sum = sum + A[i]
if sum > left-sum
left-sum = sum
max-left = i
right-sum = -∞
sum = 0
for j = mid + 1 to high
sum = sum + A[j]
if sum > right-sum
right-sum = sum
max-right = j
return (max-left, max-right, left-sum + right-sum)
以上过程花费θ(n)的时间。
有了以上线性时间的伪代码,就可以写出以下求解最大子数组问题的分治算法的伪代码了:
FIND-MAXIMUM-SUBARRAY(A, low, high)
if high == low // base case: only one element
return (low, high, A[low])
else
mid = floor((low + high) / 2) // 向下取整
(left-low, left-high, left-sum) = FIND-MAXIMUM-SUBARRAY(A, low, mid)
(right-low, right-high, right-sum) = FIND-MAXIMUM-SUBARRAY(A, mid + 1, high)
(cross-low, cross-high, cross-sum) = FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)
if left-sum >= right-sum and left-sum >= cross-sum
return (left-low, left-high, left-sum)
elseif right-sum >= left-sum and right-sum >= cross-sum
return (right-low, right-high, right-sum)
else
return (cross-low, cross-high, cross-sum)
此解法的时间复杂度为θ(nlgn)。

以上过程的C++实现:
#include <iostream>
#include <vector>
using namespace std;
int findMaxCrossSubarray(const vector<int> &nums, size_t start, size_t mid, size_t end) {
int leftSum = 0;
int sum = 0;
for (size_t i = mid + 1; i > start; --i) {
sum += nums[i - 1];
if (sum > leftSum) {
leftSum = sum;
}
}
int rightSum = 0;
sum = 0;
for (size_t i = mid + 1; i <= end; ++i) {
sum += nums[i];
if (sum > rightSum) {
rightSum = sum;
}
}
return leftSum + rightSum;
}
int findMaximumSubarray(const vector<int>& nums, size_t start, size_t end) {
if (start == end) {
return nums[start];
}
size_t mid = (start + end) >> 1;
int leftMax = findMaximumSubarray(nums, start, mid);
int rightMax = findMaximumSubarray(nums, mid + 1, end);
int crossMax = findMaxCrossSubarray(nums, start, mid, end);
return max(leftMax, max(rightMax, crossMax));
}
int main() {
vector<int> ivec = {
13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7 };
cout << findMaximumSubarray(ivec, 0, ivec.size() - 1);
}
非递归地、线性地求最大子数组,时间复杂度为O(n):
#include <iostream>
#include <vector>
#include <limits>
using namespace std;
int findMaximumSubarray(const vector<int>& nums, size_t start, size_t end) {
int sumMax = numeric_limits<int>::min();
int curSum = 0;
for (size_t i = 0; i < nums.size(); ++i) {
curSum += nums[i];
if (curSum > sumMax) {
sumMax = curSum;
}
if (curSum < 0) {
curSum = 0;
}
}
return sumMax;
}
int main() {
vector<int> ivec = {
13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7 };
cout << findMaximumSubarray(ivec, 0, ivec.size() - 1);
}
矩阵乘法伪代码:
SQUARE-MATRIX-MULTIPLY(A, B)
n = A.rows
let C be a new nXn matrix
for i = 1 to n
for j = 1 to n
cij = 0
for k = 1 to n
cij = cij + aik * bkj
return C
矩阵乘法不一定都要花费Ω(n³)时间,即使矩阵乘法的自然定义就需要进行这么多次的标量乘法,有Strassen的矩阵相乘递归算法,时间复杂度为O(n2.81)。
为简单起见,假定矩阵为nXn,其中n为2的幂,之后将nXn的矩阵划分为4个n/2Xn/2的子矩阵,一个矩阵运算性质如下:
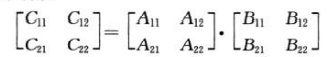
以下公式等同于上图公式:
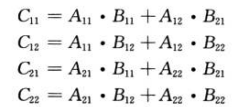
根据以上过程可写出伪代码:
SQUARE-MATRIX-MULTIPLY-RECURSIVE(A, B)
n = A.rows
let C be a new nXn matrix
if n == 1
c11 = a11 * b11
else
C11 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A11, B11) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A12, B21)
C12 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A11, B12) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A12, B22)
C21 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A21, B11) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A22, B21)
C22 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A21, B12) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A22, B22)
return C
以上代码掩盖了一个微妙但重要的细节,应如何分解矩阵,如果我们真的创建12个新的n/2Xn/2矩阵,将会花费θ(n²)时间复制矩阵元素,实际我们可以通过下标来指明一个子矩阵。
以上过程中,第五行计算分解矩阵花费θ(1)的时间,之后八次调用SQUARE-MATRIX-MULTIPLY-RECURSIVE,每次调用完成两个n/2Xn/2矩阵的乘法,因此花费总时间是8T(n/2),这一过程中,需要调用4次矩阵加法需要时间θ(n²),因此递归情况的总时间为:
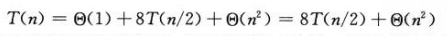
如果通过复制元素实现矩阵分解,需要的花销为θ(n²),运行总时间将会提高常数倍,T(n)不变。因此运行时间公式如下:
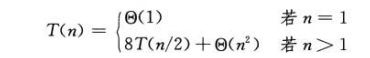
这种方法T(n)=θ(n³),因此简单的分治算法不优于直接法。
T(n)的公式中,θ(n²)实际省略了n²之前的常系数,因为θ符号已经包含所有常系数了,但公式8T(n/2)中的8不能省略,因为8表示递归树中每个节点有几个孩子节点,进而决定了树的每一层为总和贡献了多少项,如果省略了8,递归树就变为线性结构了。
Strassen算法的核心思想是令递归树稍微不那么茂盛一点,即只递归进行七次而不是八次n/2Xn/2矩阵乘法,减少一次矩阵乘法带来的代价可能是额外几次n/2Xn/2矩阵加法,但只是常数次,该算法包含以下步骤,步骤2~4会在后面说明具体步骤:
1.将矩阵按下标分解,方法与普通递归法相同,花费θ(1)的时间。
2.创建10个n/2Xn/2的矩阵,每个矩阵保存步骤1中创建的两个子矩阵的和或差,花费时间θ(n²)。
3.用步骤1中创建的子矩阵和步骤2中创建的10个矩阵,递归地计算7个矩阵积,每个矩阵积的结果都是n/2Xn/2的。
4.通过步骤3中的矩阵积的结果计算出结果矩阵C的C11、C12、C21、C22。
步骤1、2、4共花费θ(n²)时间,步骤3要求进行7次n/2Xn/2矩阵乘法,因此得到Strassen算法运行时间T(n):
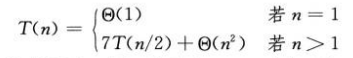
上图中T(n)=θ(nlg7),lg7在2.80到2.81之间。
Strassen算法的步骤2中,创建如下10个矩阵:
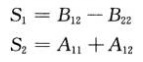
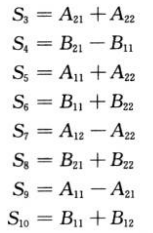
以上步骤计算了10次n/2Xn/2矩阵的加减法,花费θ(n²)时间。
步骤3中,递归地计算7次n/2Xn/2矩阵的乘法:
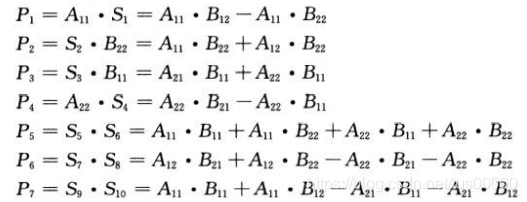
上述公式中,只有中间一列的乘法需要实际计算,右边列只是说明这些乘积与步骤2创建的子矩阵之间的关系。
步骤4对步骤3创建的矩阵进行加减法运算:
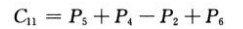
展开上述公式的右边:
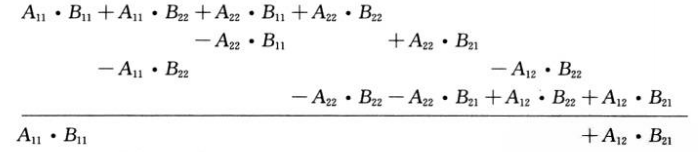
而C12等于:
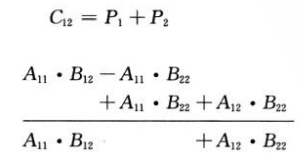
C21等于:
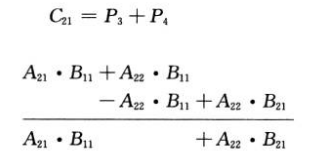
C22等于:
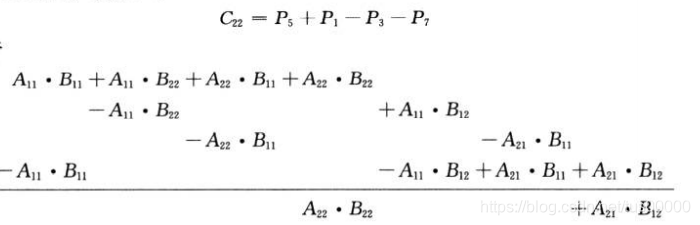
代入法求解递归式:
1.猜测解的形式。
2.用数学归纳法求出解中的常数,并证明解是正确的。
可用代入法求以下递归式的上界:
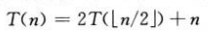
我们猜测其解为O(nlgn),代入法要求证明,恰当选择常数c>0,可有T(n)<=cnlgn,首先假定此上界对所有整数m<n都成立,特别是对于m=⌊n/2⌋,有T(⌊n/2⌋)<=c⌊n/2⌋lg(⌊n/2⌋),将其代入递归式,得到:
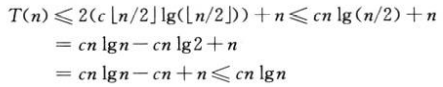
其中,只要c>=1,最后一步都会成立。数学归纳法要求证明解在边界条件下也成立,假设T(1)=1是递归式唯一的边界条件(起始条件),对n=1,边界条件T(n)<=cnlgn推导出T(1)<=c1lg1=0,与T(1)=1矛盾,此时可以扩展n,将n=2作为边界条件,由递归式可计算出T(2)=4和T(3)=5,此时可以完成归纳证明:对某个常数c>=1,T(n)<=cnlgn,方法是选择足够大的c,满足T(2)<=c2lg2和T(3)<=c3lg3。
但代入法没有通用的方法猜测递归式的正确解,猜测解要考经验,偶尔还需要创造力,可以借用递归树做出好的猜测。如果递归式与你曾见过的递归式相似,那么猜测一个类似的解是合理的,如以下递归式:
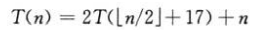
与上例相比只是多了+17,当n较大时,都是接近n的一半,因此猜测T(n)=O(nlgn),这个猜测是正确的。
另一种好的猜测方法是先证明递归式较松的上界和下界,然后缩小不确定的范围,如上例中可以从下界Ω(n)开始,因为递归式中包含n这一项,还可以证明一个上界O(n²),然后逐渐降低上界,提升下界,直至收敛到渐近紧确界θ(nlgn)。
有时猜出了渐近界,但归纳证明失败,此时修改猜测,将它减去一个低阶的项,数学证明常常能顺利进行,如以下递归式:
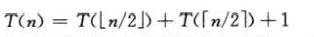
我们猜测解为T(n)=O(n),并尝试证明对某个恰当的常数c,T(n)<=cn成立,将猜测代入递归式,得到:
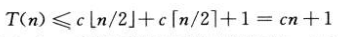
但这并不意味着对任意c,都有T(n)<cn,我们可能猜测一个更大的界,如T(n)=O(n²),虽然可以推出结果,但原来的T(n)=O(n)是正确的。
我们做出新的猜测:T(n)<=cn-d,d为≥0的一个常数,现在有:
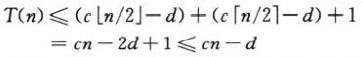
只要d≥1,此式就成立,之后与以前一样,选足够大的c处理边界条件。
你可能发现减去一个低阶项的想法与直觉相悖,毕竟,如果上界证明失败,就应该将猜测增加而非减少,但更松的界不一定更容易证明,因为为了证明一个更弱的上界,在归纳证明中也必须使用同样更弱的界。
上例中我们可能出现如下错误证明:
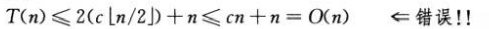
因为c为常数,错误在于我们并未证出与归纳假设严格一致的形式,即T(n)≤cn。
剩下太难了 不学了 可能以后学