目录
计算任意多边形的中心:
获取多边形外接矩形,获取最大最小XY(也就是外接矩形的四个角点的坐标:Xmax、Xmin、Ymax、Ymin)
static double XMax, XMin, YMax, YMin;
double CenterX = (XMax + XMin) / 2;
double CenterY = (YMax + YMin) / 2;计算多边形重心:
(1)划分多边形为三角形:
以多边形的一个顶点V为源点(V可取输入的第一个顶点),作连结V与所有非相邻顶点的线段,即将原N边形或分为(N-2)个三角形;
(2)求每个三角形的重心和面积:
设某个三角形的重心为G(cx,cy),顶点坐标分别为A1(x1,y1),A2(x2,y2),A3(x3,y3),则有cx = (x1 + x2 + x3)/3.同理求得cy。求面积的方法是s = ( (x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1) ) / 2,当A1,A2,A3顺时针排列时取-,否则取正(此定理不证)。事实上,在求每个三角形时不需要辨别正负,之后有方法抵消负号,见下述。
扩展:
三角形的重心:三条中线的交点。其中重心到其中一个顶点的距离是重心到该顶点对边中点的距离的2倍。
即:GC = 2 * GP,也就是说重心坐标在 CP 线段上距离 AB 的中点 P 的 1/3 处。
假设 A,B,C 三点的坐标为:
![]()

那么通过简单坐标计算,可以得出其重心坐标为(x,y)
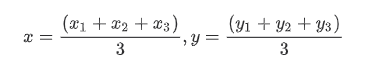
三角形面积
利用向量积来计算面积,我们知道平面中的两个向量的叉乘的模等于以这两个向量为边的平行四边形的面积,那么以这个两个向量为边的三角形,则是这个平行四边形的面积的一半。

这里给出运算草稿:
为什么这里我们会以原点作为第三个点构成三角形呢?其实是跟接下来求多边形面积是有关联的。
多边形的面积
我们在上面给出的求平面多边形重心的公式中有说到,一般我们会把多边形剖分为多个三角形。
那么这个剖分点 P 我们可以设在哪里呢?这里先给出结论:这个剖分点可以设置在多边形的内部,也可以设置到外部。

为什么这个剖分点可以设置到外部呢?我们可以通过简单的三角形情况来推广到多边形的情况。
对于三角形ABC,我们把剖分点设置在其外部 P 的一点上

向量叉积是有正负之分的,并且根据上面所说的计算三角形面积,那么以 P 为剖分点,通过向量积可以得出这个三角形的面积 A 为:

因为 向量PB 在 向量PA 的顺时针方向,所以 PA→×PB→ 的结果是负数的。那么上面的面积计算公式其实就可以理解为:
三角形ABC的面积 = 三角形PBC面积 + 三角形PCA面积 - 三角形PAB面积
假设这四个点的坐标为:
![]()
通过上面的公式进行计算,具体的演算过程我就不给出了,这里直接给出计算结果:

我们可以发现,计算结果中没有 x0,y0 的项,因为它们在计算过程中给消去了,数学就是这么奇妙!所以我们可以得出一个结论,多边形的面积结果与这个剖分点的位置是无关的。那么为了计算方便,我们当然选择把这个 P 点设置到原点上啦。
那么只要我们知道多边形的每一个顶点,通过原点进行剖分成多个三角形,然后通过向量的叉乘求出每个三角的面积,最后相加,就可以求出多边形的面积了。
(3)求原多边形的重心:
公式:cx = (∑ cx[i]*s[i]) / ∑s[i]; cy = (∑ cy[i]*s[i] ) / ∑s[i];其中(cx[i], cy[i]), s[i]分别是所划分的第i个三角形的重心坐标和面积。在(2)中求每个重心坐标时要除以3,实际上不需要在求每个三角形坐标时都除以3,只需要求出∑ cx[i]*s[i]后一次性除以3即可。即是多边形重心坐标变为:cx = (∑ cx[i]*s[i]) / (3*∑s[i]); cy = (∑ cy[i]*s[i] ) / (3*∑s[i]);
总结:
每个三角形重心:cx = x1 + x2 + x3;cy同理。
每个三角形面积:s = ( (x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1) ) / 2;
多边形重心:cx = (∑ cx[i]*s[i]) / (3*∑s[i]); cy = (∑ cy[i]*s[i] ) / (3*∑s[i]);
private void GetGravityPoint(List<PolyPoint> lstPol)
{
double n, i;
double x1, y1, x2, y2, x3, y3;
double sum_x = 0, sum_y = 0, sum_s = 0;
n =int.Parse(Console.ReadLine());
//x1 = int.Parse(Console.ReadLine());
//y1 = int.Parse(Console.ReadLine());
//x2 = int.Parse(Console.ReadLine());
//y2 = int.Parse(Console.ReadLine());
x1 = lstPol[0].xPoint;
y1 = lstPol[0].yPoint;
x2 = lstPol[1].xPoint;
y2 = lstPol[1].yPoint;
n = lstPol.Count;
int k = 2;
for (i = 1; i <= n - 2; i++)
{
//x3 = int.Parse(Console.ReadLine());
//y3 = int.Parse(Console.ReadLine());
x3 = lstPol[k].xPoint;
y3 = lstPol[k].yPoint;
double s = ((x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1)) / 2.0;
sum_x += (x1 + x2 + x3) * s;
sum_y += (y1 + y2 + y3) * s;
sum_s += s;
x2 = x3;
y2 = y3;
k++;
}
Console.WriteLine("重心为:%.2lf , %.2lf\n", sum_x / sum_s / 3.0, sum_y / sum_s / 3.0);
}
Reference: