文章目录
关于计算机中“码”的设计根源的浅薄理解
无论是在学习大学计算机这门课,还是在学习计算机系统的初期,我们都会反复提到关于几种码的定义。这里我单指原码、反码和补码,而并不包括国标码和机内码那几种码。尝试理解设计师们在初期为什么要设计原码、反码和补码,一定能让我们对这三个好兄弟(gui)有更好的理解。
完整的读完本篇文章,你对码的理解一定能提高相当高的一个层次。
发表意见仅代表个人理解,如果出现一些错误和理解上的局限请各位客官不吝赐教。
从计算而设计的角度出发
关于为什么计算机要使用二进制,引用一篇本站阅读量很高的一篇文章,此处不再重复。【为什么计算机要使用二进制】
在这里我们从如何计算开始,试图从零开始教一台电脑做数学题。
众所周知:计算机是一个非常“蠢”的家伙,但是他是最勤劳的。我们总要交给他尽量简单的方法和动作驱使他最大效率的工作,来满足我们自己的需求,因此设计一个通用且简单的逻辑始终是我们的核心目的。
加法
我们先创建两个只有16位二进制(远古电脑的字长)的非负整数吧,做一下加法。
| num1 | num2 | sum |
|---|---|---|
| 0000000000000001 | 0000000000000011 | 0000000000000100 |
这个和我们的十进制加法除了进制不同以外,计算方式和规则其实是一模一样的,对于习惯了十进制的“碳基生物”们来说也十分的“自然”(指自然语言的那种自然)。
而且由于二进制的特性,使加法运算的图灵机逻辑也变的十分简单。因此加法计算也一直被保留到今天,每天在计算机里进行难以计数的循环。
因此我们愿意也可以、更应该把正数用普通的二进制表示在计算机里。
减法
什么是减法?是a-b吗?
什么叫做a-b?那么-b到底是什么?
你可能会很疑惑我为什么要问这个问题,你可以先用一分钟仔细思考一下到底-b是什么,或者说,-1是什么。
关于负数,这里引用一段百度百科的解释:
负数是数学术语,比0小的数叫做负数,负数与正数表示意义相反的量。负数用负号(Minus Sign,即相当于减号)“-”和一个正数标记,如−2,代表的就是2的相反数。于是,任何正数前加上负号便成了负数。一个负数是其绝对值的相反数。在数轴线上,负数都在0的左侧,最早记载负数的是我国古代的数学著作《九章算术》。在算筹中规定"正算赤,负算黑",就是用红色算筹表示正数,黑色的表示负数。两个负数比较大小,绝对值大的反而小。
我们关注到这一段里面比较关键的几句话:
负数与正数表示意义相反的量。负数用负号(Minus Sign,即相当于减号)“-”和一个正数标记,如−2,代表的就是2的相反数。于是,任何正数前加上负号便成了负数。
负数用负号“-”和一个正数标记,代表的就是2的相反数。也就是说我们在扩展负数的时候,只是为了引出一种数字或者说一种“东西”可以与它相对应的正数相加,从而抵消获得零的结果。
那么,如果我们从现在开始忘记平日里负数的表现形式(它只是一个抽象单位的“名字”罢了)——加负号,我们该如何给计算机设计一个所谓的负数来让它代替自然语言中的-a呢?
我们仍旧是从我们设计负数机内表示的初衷出发:一种数字或者一个东西可以与他相对应的正数相加等于零。
我们看一下下面的表格。
| num1 | num2 | sum |
|---|---|---|
| 0000000000010101 | ? | 0000000000000000 |
用我们学过的二进制计算方法告诉自己num2应该是多少:
1111111111101011
如果你是揣着问题来寻求答案的,你这里应该已经想到了:所以我们为什么补码要用取反加一的操作呢?
首先二进制数是“非黑即白”的,也就是一个数位上要么是1要么是0。
对于计算机来说取反的任务十分简单,我们只需要用每位取反操作,就可以创造一个新数,让它和原来的数字相加,结果等于一串全是1的最大值,这就是我们的反码。
然后我们再对反码加一,即补码:让我们的补码正好可以和对应的正数“互补”得和为0,即对这个“1111111111111111”加1,就可以像多米诺骨牌一样把所有的1变成0(最高位的1溢出字节存储的范围),从而把整个数字串变成“0000000000000000”。
到目前为止,我们的减法需求已经满足了,对吗?
显然不是,我们会意识到一个问题:按照我们上面的逻辑1100100000011001到底是一个正数,还是一个“负数”呢?
计算用码和自然数字的双射
只要我们用补码计算,我们就一定逃不了这个问题:我们计算的终点是将计算结果拿来使用:我们几乎一定需要把数字转化成我们的自然十进制使用,如果我们都分不清一个存在计算机里的数字到底是用来表示正数还是负数,自然是不可行的。
那么怎么样在计算机内表示的正数和负数之间用一个最简单的逻辑区分他们,使得他们都可以不混淆的、一对一的转化成自然数字。
很简单,大家都能轻松想到,而且我们也记得,那就是用最前面的符号位作为一个“标记”,也就是给正和负划分各自的领地。
二进制非黑即白,我们用0表示正数还是用1表示负数呢?
我在自己这几天相关的学习中做了一张图,可以让大家更清楚的明白整个整数的表示。
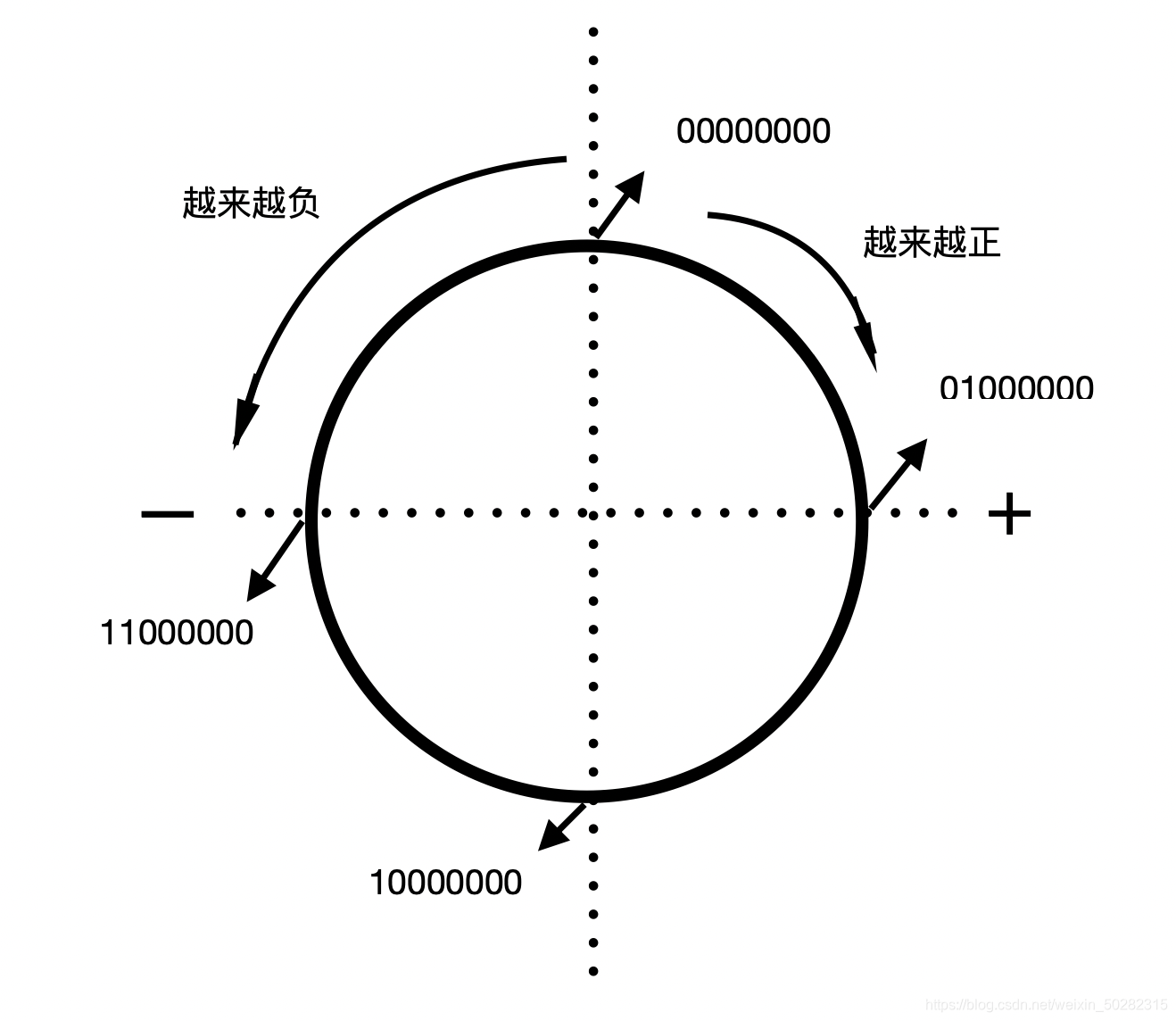
为什么选择第一位为0对应“正”,为1对应“负”呢?这要从我们创造这个规则的需求说起:我们能不能用这样的对应规则,使得它能满足一切的整数加法(减法已经化为加法)计算呢?
当我们用任何一个数去加上另一个数的时候:我们找到第一个数字在图上的位置,然后我们把第二个数字的加入用对第一个数字位置的变换表示出来:即正数是顺时针移动对应的角度,负数也是顺时针移动一个更大的角度,而这个角度在圆里正好可以看作是逆时针移动这个负数对应的正数角度(我们可以把这个加看做是一个矢量的加)。
因此我们无论是加上一个正数还是一个负数的问题都可以迎刃而解。
而我们图中00000000对应的值即是0,在它的左右划分了正和负。
我们在做任何正负数字的加法的时候,在范围内越过00000000的这个界限只是和的符号的正常变化。
我们也可能会思考一个问题:你说正在右,负在左,那么要是正加正或者是负加负越过了正和负的界限的时候,即10000000,会发生什么事?
回答:会出错。。。
所以我们的所谓的数值溢出(这里指的是数值过大超过了我们一个int或float的表示范围)也是这样产生的,两个正数的值相加进位到第一位------影响了我们用来区分正负范围的数位,自然会引起错误的反应。
溢出(超过一个字节能够表示的范围)
计算机取模操作的一种艺术。我们用字节存储的限制,成功的把我们本来表示正负数字的一维数轴首尾相连变成了如上图的一个圆圈。
我们会在很多博客与文章中看到关于取模的“表盘”的比喻,我觉得很精妙(也是启发我做上方做这个圆圈的源头)。溢出是一个物理层面的必然,在一定程度上来说其实是计算机计算的枷锁。
但是我们可以利用这种枷锁来创造我们想要的某种计算,并且不需要创造新的规则。
所以我觉得它是一种艺术。按王进喜的话来讲,就是一种有条件要上,没有条件创造条件也要上的精神。
在这里就不再多讲关于溢出的问题,因为我对于也了解不够深入,有兴趣的同学可以自己查阅相关的文章。
我们应该能想到的东西
本质上来说,所谓的原码、补码、反码都是所谓的名字的问题:我们唯一且最终的目的就是创造一种可以通用的用来做"加法"的二进制表示方式罢了。
原码是数字的真值,反码是求补码的一个工具码(完全的中间产物),补码是我们最终的产物。
至此,我们的计算机最基础的几种码都弄明白了。在此基础上的整数乘法和除法都和加法离不开干系。
完结撒花花!!!
在文章后面说的一些话
本文不会谈及每一种码,一是自己也暂且没有做过多的了解,另外是篇幅和精力限制(本文已经拖延了一个星期了)。
我只想要谈及一些小小的问题。
如果在你在看完了上文这么长的内容后,我们应该思考的问题
为什么我们要按照IEEE的一些看起来似乎不符合我们逻辑的规则行事?
在IEEE754 中,为什么浮点数移码的尾码不需要用补码表示?为什么移码的阶数要用真值加上127的转化而不是用带符号位的补码来表示,这样不是更直观吗?
浮点数的计算和整数的计算有哪些区别,因此浮点数的表示产生了哪些改变,这些改变是为了什么目的?又有哪些精妙的设计是我们仅仅理解就需要一定时间的?
以及更多更多的数值计算和逻辑计算到底有哪些区别?他们的区别到底为何而生?
这些问题我不会给出我自己的理解,如果有看官想要确定自己的想法也可以在评论区给出自己的理解,让更多的有识之士一起赏评一些,必能裨补阙漏,有所广益。
“提出一个问题往往比解决一个问题更重要,因为解决问题也许仅能是一个数学上或实验室上的技能而已。而提出新的问题、新的可能性,从新的角度去看旧的问题,都需要有创造性的想象力,而且标志着科学的真正进步。” ------爱因斯坦
个人始终认为问题或需求导向的求解才是才是最正确且不多余的。我们在有能力提出没有解答的问题之前,可以多尝试一下从已存的解答中试图复原其最初的诉求。我们一定能因此提高我们自己创造问题解决问题的能力。
谢谢大家赏识读到最好,祝一帆风顺!