逻辑回归公式推导

1、逻辑回归模型假设是： $h\theta (x)=g(\theta \top x)$ ，其中X代表特征向量，g代表逻辑函数(logistic function)是一个常用的为S形的逻辑函数，公式为： $\ g(z) = \frac{1}{1+e^{-z}}$ ，该逻辑函数的图像为：

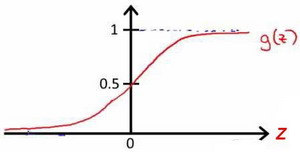
由于g(z)函数的值域为0-1，则对于该 $h \theta (x)$ 的理解为：对于给定的输入变量，根据选择的参数计算输出变量=1的可能性（estimated probablity）即 $h \theta(x)=P(y=1|x; \theta)$ 。例如，如果对于给定的x ，通过已经确定的参数计算得出hθx=0.7 ，则表示有70%的几率y 为正向类，相应地y 为负向类的几率为1-0.7=0.3。

2、模型函数确定之后就需要确定损失函数了，损失函数就是用来衡量模型的输出与真实输出的差别。

假设只有两个标签1和0， $yn\in \left \{ 0 ,\right 1\}$ 。我们把采集到的任何一组样本看做一个事件的话，那么这个事件发生的概率假设为p。我们的模型y的值等于标签为1的概率也就是p。

$p_{y=1}= \frac{1}{ 1 + e^{- \theta \top x}}=P$ $P_{y=1} = \frac{1}{1+e^{-\theta\top x}} = P$

因为标签不是1就是0，因此标签为0的概率就是： $P_{y=0} = 1-P$

我们把单个样本看做一个事件，那么这个事件发生的概率就是：

$P_{(y|x))} = \left\{\begin{matrix} p, y=1& \\ 1-p, y=0& \end{matrix}\right.$

这个函数不方便计算，它等价于:

$P_{y_{i}|x_{i}} = p^{y_{i}} * (1-P)^{1-y_{i}}$

解释下这个函数的含义，我们采集到了一个样本 $\left ( x_{i}, \right y_{i} )$ ，对这个样本，它的标签是 $y_{i}$ 的概率是 $p^{y_{i}}(1-p)^{1 - y_{i}}$ 。（当y=1，结果是p；当y=0，结果是1-p）。

如果我们采集到了一组数据一共N个， $\left \{ (x_{1}, y_{1}), (x_{2}, y_{2}), (x_{3}, y_{3})...(x_{N}, y_{N}) \right \}$ ，这个合成在一起的合事件发生的总概率怎么求呢？其实就是将每一个样本发生的概率相乘就可以了，即采集到这组样本的概率：

$P_{total} = P (y_{1}|x_{1} )P (y_{2}|x_{2} )P (y_{3}|x_{3} )...P (y_{N}|x_{N} )$

$= \prod_{n=1}^{N} p^{y_{n}} (1-p)^{1-y_{n}}$

由于连乘很复杂，我们通过两边取对数来把连乘变成连加的形式，即：

$ln(P_{total})=ln(\prod_{n=1}^{N} p^{y_{n}} (1-p)^{1-y_{n}})$

$=\sum_{n=1}^{N}ln(p^{y_{n}} (1-p)^{1-y_{n}})$

$=\sum_{n=1}^{N} (y^{n}ln(p) + (1-y_{n})ln(1-p))$

其中 $p=\frac{1}{1+e^{-\theta} \top x}$

这个函数 $J(\theta)$ 又叫做它的损失函数。损失函数可以理解成衡量我们当前的模型的输出结果，跟实际的输出结果之间的差距的一种函数。这里的损失函数的值等于事件发生的总概率，我们希望它越大越好。但是跟损失的含义有点儿违背，因此也可以在前面取个负号。所以： $J(\theta)=- \frac{1}{n} \sum_{n=1}^{N} (y^{n}ln(p) + (1-y_{n})ln(1-p))$

3、根据以上我们知道了逻辑回归的梯度损失函数 $J(\theta)$ ，则可以通过求对 $\theta$ 的偏导得到 $J(\theta)$ 的梯度函数。

$\bigtriangledown p(\theta)=\bigtriangledown (\frac{1}{1+e^{-\theta\top x}})$

$=- \frac{1}{(1+e^{-\theta\top x})^{2}} (1+e^{-\theta\top x})'$

$=- \frac{e^{-\theta\top x}}{(1+e^{-\theta\top x})^{2}} \cdot (-x)$

$=\frac{1}{1+e^{-\theta\top x}} \cdot \frac{e^{-\theta\top x}}{1+e^{-\theta\top x}} \cdot x$

$=p(1-p)x$

在对 $J(\theta)$ 求导的时候带入 $\bigtriangledown p(\theta)$ 可得以下：

$\bigtriangledown J(\theta) = \bigtriangledown -\frac{1}{m} (\sum_{n=1}^{N}( y_{n}ln(p) + (1-y_{n})ln(1-p)))$

$=\sum_{n=1}^{N} (y_{n}ln'(p) + (1-y_{n})ln'(1-p))$
$=-\frac{1}{n}\sum_{n=1}^{N} ((y_{n}\frac{1}{p}p') + (1+y_{n})\frac{1}{1-p}(1-p'))$

$=-\frac{1}{n}\sum_{n=1}^{N} (y_{n}(1-p)x_{n} - (1-y_{n}px_{n}))$

$=-\frac{1}{n}\sum_{n=1}^{N} (y_{n} - p)x_{n}$

$=-\frac{1}{n}\sum_{n=1}^{N}(y_{n} - \frac{1}{1+e^{-\theta \top x_{n}}})x_{n}$

$=\frac{1}{n}\sum_{n=1}^{n} ( \frac{1}{1+e^{-\theta\top x_{n})}} - y_{n})x_{n}$

4、根据以上就可得到逻辑回归的定义：
目标函数： $h_{\theta}(x)=\frac{1}{1+e^{-\theta\top x}}$

代价函数： $J(\theta)=- \frac{1}{m} \sum_{n=1}^{N} (y^{n}ln(p) + (1-y_{n})ln(1-p))$

梯度函数： $\frac{\partial J(\theta)}{\partial \theta} = \frac{1}{n}\sum_{n=1}^{n}(\frac{1}{1+e^{-\theta\top x_{n}}} - y_{n})x_{n}$

梯度下降过程：

梯度下降公式为：

$\theta_{j} := \theta_{j} - \alpha \frac{1}{m} \sum_{n=1}^{N}(h_{\theta}(x^{(n)}) - y^{(n)})x_{j}^{(n)}$ 其中的 $\alpha$ 为学习率，可以选择的有：0.01，0.03，0.1，0.3，1，3，10

参考自：https://zhuanlan.zhihu.com/p/44591359

逻辑回归公式推导

猜你喜欢