1.面板数据模型理论--变截距面板数据模型

变截距面板数据模型

变截距面板数据模型理论介绍

混合效应模型

背景思想

回归公式可以忽略个体与时间变化的差异，因此所有的数据特征可以通过一个公式进行刻画。进行数据的大杂烩、乱炖。为什么采取这么直接粗暴的方式呢？因为每个品种的菜(个体与时间维度)都很少，每一个品种的菜都不能够做出完整一盘菜，只能将所有的菜杂七杂八的混合起来乱炖。乱炖虽说精度不高，可是总比没法处理要好很多。

模型假定

1.$E({\epsilon }_{it})=0$;
2.$var(\epsilon )={\sigma }_{\epsilon }为常数$；
3. ${\epsilon }_{it}与X_{it}不相关$;

公式：

$Y_{it}=\alpha +X_{it}^{\prime }\beta +{\epsilon }_{it},i=1,2,3,...,N;t=1,2,3,...,T$

项目	含义
$i$	个体标志序数
$t$	时间序数
$X_{it}$	观测变量，$K\ast 1$向量，$(X_{1it,},X_{2it},..,X_{kit}{)}^{\prime }$
$\beta$	参数，$K\ast 1$向量, $({\beta }_1,{\beta }_2,..,{\beta }_k{)}^{\prime }$
$\alpha$	截距项
${\epsilon }_{it}$	随机扰动项

估计方法展示

数据结构展示：

估计方法：

这个模型是将所有的数据$(y,x_1,x_2,x_3,x_4)$，直接导入公式$Y_{it}=\alpha +X_{it}^{\prime }\beta +{\epsilon }_{it},i=1,2,3,...,N;t=1,2,3,...,T$进行回归，只能求出一组$({\beta }_1,{\beta }_2,..,{\beta }_k{)}^{\prime }$，意味着$\beta$在不同个体、不同时点上都是同一组，它不会因为时间或个体而发生变动。

固定效应模型

背景思想

有一些影响因素A随着一些条件的改变而改变，但是这个因素A并未通过$X$观测变量纳入模型，比如说我们研究消费函数，$C=\alpha +\beta Y+\epsilon$, 这里的$\alpha$叫做自发消费，这个自发性消费是可能和个人特征、所处的社会文化、教育等未观测变量有关，换句话说，截距项 $\alpha$ 和个体某些未观测到的特质有关，而不和$Y$有关。$\alpha$和$\epsilon$都是代表了不可观测因素的影响，前者的影响因素是有趋势的(常数也是一种趋势)，后者的影响因素是无趋势的。更简单的理解就是，$\alpha$存在的意义就是为了使$\epsilon$拥有零均值。

• 当这个截距项与个体特征相关时，我们称为个体固定效应模型。
• 当这个截距项与时间特征有关时，我们称为时间固定效应模型。
• 同理，和A潜在变量有关，我们就可以称它为A的固定效应模型。
• 当这个截距项与个体特征和时间特征都相关时，我们称为双固定效应模型。
• 同理，也可以同时依据三种或三种以上的变量进行分类，回归得出它们影响的截距项的估计值。

个体固定效应模型

模型假设

1.$E({\epsilon }_{it})=0$;
2.$var(\epsilon )={\sigma }_{\epsilon }为常数$；
3 ${\epsilon }_{it}与X_{it}不相关$;
4. ${\alpha }_i与X_{it}相关$
5. $E({\alpha }_i)=0$

模型公式

$Y_{it}={\alpha }_0+{\alpha }_i+X_{it}^{\prime }\beta +{\epsilon }_{it},i=1,2,3,...,N;t=1,2,3,...,T$

项目	含义
$i$	个体标志序数
$t$	时间序数
$X_{it}$	观测变量，$K\ast 1$向量，$(X_{1it,},X_{2it},..,X_{kit}{)}^{\prime }$
$\beta$	参数，$K\ast 1$向量, $({\beta }_1,{\beta }_2,..,{\beta }_k{)}^{\prime }$
${\alpha }_0$	常数项
${\alpha }_i$	个体效应
${\alpha }_0+{\alpha }_i$	截距项
${\epsilon }_{it}$	随机扰动项

补充：也写为
$Y_{it}=u_i+X_{it}^{\prime }\beta +{\epsilon }_{it},i=1,2,3,...,N;t=1,2,3,...,T$
$u_i={\alpha }_0+{\alpha }_i,E(u_i)={\alpha }_0,E({\alpha }_i)=0$

估计方法展示

数据结构如下：

1.组内（within）估计（离差估计）
离差估计就是剔除常数项，然后进行估计，首先明白我们的目标：分别计算$a,b,c,d,e$组内的截距和各自的组内$\beta$ .其实，不需要离差就可以回归。将a,b,c,d,e组的数据分别带入$Y_{it}={\alpha }_0+{\alpha }_i+X_{it}^{\prime }\beta +{\epsilon }_{it},i=1,2,3,...,N;t=1,2,3,...,T$，就可以得到结果。

• 离差方差推导
  原方程：
  $Y_{it}={\alpha }_0+{\alpha }_i+X_{it}^{\prime }\beta +{\epsilon }_{it},i=1,2,3,...,N;t=1,2,3,...,T$
  求均值方程：
  ${\bar{Y}}_i={\alpha }_0+{\alpha }_i+{\bar{X}}_i^{\prime }\beta +{\bar{\epsilon }}_i,i=1,2,3,...,N;t=1,2,3,...,T$
  离差变换（原方程减均值方程）：
  $Y_{it}-{\bar{Y}}_i={\alpha }_0+{\alpha }_i-({\alpha }_0+{\alpha }_i)+X_{it}^{\prime }\beta -{\bar{X}}_i^{\prime }\beta +{\epsilon }_{it}-{\bar{\epsilon }}_i=X_{it}^{\prime }\beta -{\bar{X}}_i^{\prime }\beta +{\epsilon }_{it}-{\bar{\epsilon }}_i,i=1,2,3,...,N;t=1,2,3,...,T$
  ${\bar{Y}}_i=\frac{1}{T}\sum _{t=1}^T(Y_{it})$
  ${\bar{X}}_i=\frac{1}{T}\sum _{t=1}^T(X_{it})$

• 带入离差数据求解,文字描述
  通过$(y,x_1,x_2,x_3,x_4)$计算组内时间上的均值$\overline{(y,x_1,x_2,x_3,x_4)}$，然后计算离差$(y,x_1,x_2,x_3,x_4)-\overline{(y,x_1,x_2,x_3,x_4)}$,带入离差方程$Y_{it}-{\bar{Y}}_i=X_{it}^{\prime }\beta -{\bar{X}}_i^{\prime }\beta +{\epsilon }_{it}-{\bar{\epsilon }}_i,i=1,2,3,...,N;t=1,2,3,...,T$进行估计。

• 利用估计出的$\beta$带入均值方程${\bar{Y}}_i={\alpha }_0+{\alpha }_i+{\bar{X}}_i^{\prime }\beta +{\bar{\epsilon }}_i,i=1,2,3,...,N;t=1,2,3,...,T$，求解组内的(${\alpha }_0+{\alpha }_i$)

• 通过上一步$N$个组的(${\alpha }_0+{\alpha }_i$)，求解${\alpha }_0=\frac{1}{N}\sum _{t=1}^N({\alpha }_0+{\alpha }_i)$,依据假设5：$E({\alpha }_i)=0$

• 再求解${\alpha }_i=({\alpha }_0+{\alpha }_i)-{\alpha }_0$

2.一阶差分估计
原理： 因为${\alpha }_0+{\alpha }_i$是不受时间影响的，所以我们可以使用差分方法消去常数项

• 差分方程推导
  原方程：
  $Y_{it}={\alpha }_0+{\alpha }_i+X_{it}^{\prime }\beta +{\epsilon }_{it},i=1,2,3,...,N;t=1,2,3,...,T$
  上一期方程：
  $Y_{i,t-1}={\alpha }_0+{\alpha }_i+X_{i,t-1}^{\prime }\beta +{\epsilon }_{i,t-1},i=1,2,3,...,N;t=1,2,3,...,T$
  原方程减上一期方程：
  $Y_{it}-Y_{i,t-1}={\alpha }_0+{\alpha }_i+X_{it}^{\prime }\beta +{\epsilon }_{it}-{\alpha }_0-{\alpha }_i-X_{i,t-1}^{\prime }\beta -{\epsilon }_{i.t-1}=X_{it}^{\prime }\beta -X_{i,t-1}^{\prime }\beta +{\epsilon }_{it}-{\epsilon }_{i,t-1}$
• 数据代入求解即可。
• 此方法无法求解截距项。

3.LSDV(最小二乘虚拟变量法)
学过计量的小伙伴们应该熟悉虚拟变量法，将个体差异以截距项形式的虚拟变量加入。
估计方程形式：
$Y=D\alpha +X\beta +\epsilon$
$D=\left(\begin{array}{ccccc}{D}_1& D_2& D_3& ...& D_N\end{array}\right)$
其中：
$D_N=\{\begin{array}{ll}1& \text{if }为N组\\ 0& \text{if }不为N组\end{array}$

时点固定效应模型

模型假设

1.$E({\epsilon }_{it})=0$;
2.$var(\epsilon )={\sigma }_{\epsilon }为常数$
3 ${\epsilon }_{it}与X_{it}不相关$;
4. ${\lambda }_t与X_{it}相关$；

模型公式

$Y_{it}={\lambda }_0+{\lambda }_t+X_{it}^{\prime }\beta +{\epsilon }_{it},i=1,2,3,...,N;t=1,2,3,...,T$

项目	含义
$i$	个体标志序数
$t$	时间序数
$X_{it}$	观测变量，$K\ast 1$向量，$(X_{1it,},X_{2it},..,X_{kit}{)}^{\prime }$
$\beta$	参数，$K\ast 1$向量, $({\beta }_1,{\beta }_2,..,{\beta }_k{)}^{\prime }$
${\lambda }_0$	常数项
${\lambda }_t$	时间效应
${\lambda }_0+{\lambda }_t$	截距项
${\epsilon }_{it}$	随机扰动项

估计方法展示

数据结构如下：

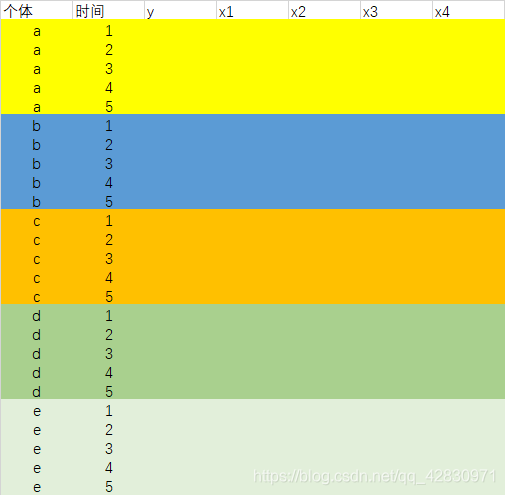
LSDV(最小二乘虚拟变量法)
学过计量的小伙伴们应该熟悉虚拟变量法，将时间段以截距项形式的虚拟变量加入。
估计方程形式：
$Y=D\lambda +X\beta +\epsilon$
$D=\left(\begin{array}{ccccc}{D}_1& D_2& D_3& ...& D_T\end{array}\right)$
其中：
$D_T=\{\begin{array}{ll}1& \text{if }为T时期\\ 0& \text{if }不为T时期\end{array}$

个体时点固定效应模型

模型假设

1 $E({\epsilon }_{it})=0$;
2 $var(\epsilon )={\sigma }_{\epsilon }为常数$
3 ${\epsilon }_{it}与X_{it}不相关$;
4 ${\lambda }_t与X_{it}相关$；
5 ${\alpha }_i与X_{it}相关$；
6 $E({\alpha }_i)=0$；
7 $E({\lambda }_i)=0$；

这里我们设定：
${\tilde{\alpha }}_i={\alpha }_0+{\alpha }_i;{\tilde{\lambda }}_t={\lambda }_0+{\lambda }_t$;
8 $E({\tilde{\alpha }}_i)={\alpha }_0$;
9 $E({\tilde{\lambda }}_i)={\lambda }_0$;

模型公式

$Y_{it}=({\alpha }_0+{\lambda }_0)+{\alpha }_i+{\lambda }_t+X_{it}^{\prime }\beta +{\epsilon }_{it}$
$={\alpha }_0+{\alpha }_i+{\lambda }_0+{\lambda }_t+X_{it}^{\prime }\beta +{\epsilon }_{it}$
$={\tilde{\alpha }}_i+{\tilde{\lambda }}_i+X_{it}^{\prime }\beta +{\epsilon }_{it},i=1,2,3,...,N;t=1,2,3,...,T$

项目	含义
$i$	个体标志序数
$t$	时间序数
$X_{it}$	观测变量，$K\ast 1$向量，$(X_{1it,},X_{2it},..,X_{kit}{)}^{\prime }$
$\beta$	参数，$K\ast 1$向量, $({\beta }_1,{\beta }_2,..,{\beta }_k{)}^{\prime }$
${\lambda }_0$	时间效应的常数项
${\lambda }_t$	时间效应
${\alpha }_0$	个体特征的常数项
${\alpha }_i$	个体效应
${\alpha }_0+{\alpha }_i+{\lambda }_0+{\lambda }_t$	截距项
${\epsilon }_{it}$	随机扰动项

估计方法

数据结构展示：

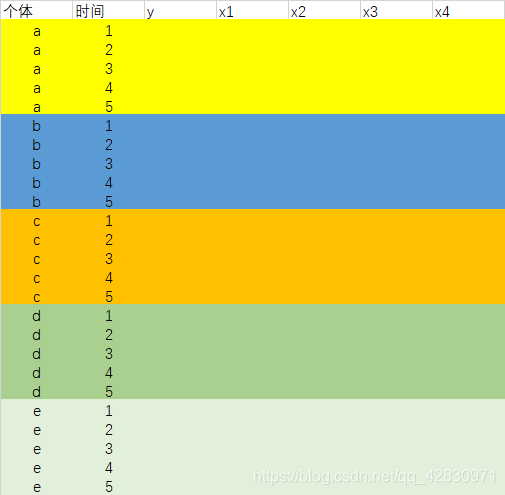
LSDV(最小二乘虚拟变量法)
学过计量的小伙伴们应该熟悉虚拟变量法，将时间段以截距项形式的虚拟变量加入。

• 估计方程形式：
  $Y=D_{\lambda }\lambda +D_{\alpha }\alpha +X\beta +\epsilon$
  $D_{\lambda }=\left(\begin{array}{ccccc}{D}_1& D_2& D_3& ...& D_T\end{array}\right)$
  其中：
  $D_T=\{\begin{array}{ll}1& \text{if }为T时期\\ 0& \text{if }不为T时期\end{array}$
  $D_{\alpha }=\left(\begin{array}{ccccc}{D}_1& D_2& D_3& ...& D_N\end{array}\right)$
  其中：
  $D_N=\{\begin{array}{ll}1& \text{if }为N组\\ 0& \text{if }不为N组\end{array}$

• 也可以将时间与个体效应混合
  $Y=Dh+X\beta +\epsilon$
  $D=\left(\begin{array}{ccccc}{D}_1& D_2& D_3& ...& D_{N\ast T}\end{array}\right)$
  其中：
  $D=\{\begin{array}{ll}1& \text{if }为第N个体的T时期\\ 0& \text{if }不为第N个体的T时期\end{array}$

个体时点双固定效应，控制区域、行业等模型

模型假设

1 $E({\epsilon }_{it})=0$;
2 $var(\epsilon )={\sigma }_{\epsilon }为常数$
3 ${\epsilon }_{it}与X_{it}不相关$;
4 ${\lambda }_t与X_{it}相关$；
5 ${\alpha }_i与X_{it}相关$；
6 $E({\alpha }_i)=0$；
7 $E({\lambda }_t)=0$；

这里我们设定：
${\tilde{\alpha }}_i={\alpha }_0+{\alpha }_i;{\tilde{\lambda }}_i={\lambda }_0+{\lambda }_t$;
8 $E({\tilde{\alpha }}_i)={\alpha }_0$;
9 $E({\tilde{\lambda }}_t)={\lambda }_0$;

模型公式

$Y_{it}={\tilde{\alpha }}_i+{\tilde{\lambda }}_t+D_{type}\gamma +X_{it}^{\prime }\beta +{\epsilon }_{it},i=1,2,3,...,N;t=1,2,3,...,T$

这个方程为了方便理解而设定，其中${\tilde{\alpha }}_i与D_{type}$存在共线性问题，毕竟类型属性也是个体特征的一部分嘛！

项目	含义
$i$	个体标志序数
$t$	时间序数
$X_{it}$	观测变量，$K\ast 1$向量，$(X_{1it,},X_{2it},..,X_{kit}{)}^{\prime }$
$\beta$	参数，$K\ast 1$向量, $({\beta }_1,{\beta }_2,..,{\beta }_k{)}^{\prime }$
${\lambda }_0$	时间效应的常数项
${\lambda }_t$	时间效应
${\alpha }_0$	个体特征的常数项
${\alpha }_i$	个体效应
${\alpha }_0+{\alpha }_i+{\lambda }_0+{\lambda }_t$	截距项
${\epsilon }_{it}$	随机扰动项
$D_{type}$	类型的虚拟变量

估计方法展示

数据展示

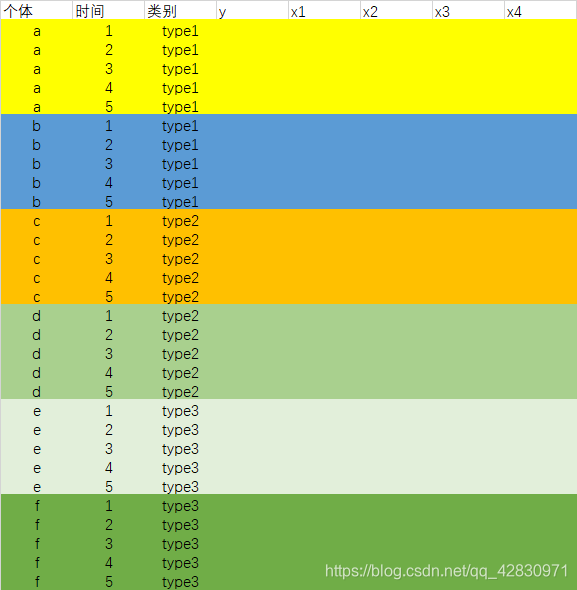
估计方法：同上，将类型变量按照虚拟变量加入方程即可。

随机效应模型

背景思想：每组估计值的截距项的变动不与X的特征有关。

个体随机效应

模型假设

1.$E({\epsilon }_{it})=0$;
2.$var({\sigma }_{\epsilon })为常数$；
3 ${\epsilon }_{it}与X_{it}不相关$;
4. ${\alpha }_i与X_{it},{\epsilon }_{it}不相关$;
5. ${\alpha }_i\sim i.i.d(0,{\sigma }_{\alpha }^2)$;

公式：

$Y_{it}={\alpha }_0+{\alpha }_i+X_{it}^{\prime }\beta +{\epsilon }_{it},i=1,2,3,...,N;t=1,2,3,...,T$
$={\alpha }_0+X_{it}^{\prime }\beta +({\alpha }_i+{\epsilon }_{it}),i=1,2,3,...,N;t=1,2,3,...,T$
$={\alpha }_0+X_{it}^{\prime }\beta +v_{it},v_{it}={\alpha }_i+{\epsilon }_{it},i=1,2,3,...,N;t=1,2,3,...,T$

项目	含义
$i$	个体标志序数
$t$	时间序数
$X_{it}$	观测变量，$K\ast 1$向量，$(X_{1it,},X_{2it},..,X_{kit}{)}^{\prime }$
$\beta$	参数，$K\ast 1$向量, $({\beta }_1,{\beta }_2,..,{\beta }_k{)}^{\prime }$
${\alpha }_0$	常数项
${\alpha }_i$	随机效应
${\alpha }_0+{\alpha }_i$	截距项
${\epsilon }_{it}$	随机扰动项
$v_{it}={\alpha }_i+{\epsilon }_{it}$	新的随机扰动项

根据$v_{it}={\alpha }_i+{\epsilon }_{it}$；${\alpha }_i\sim i.i.d(0,{\sigma }_{\alpha }^2)$;${\alpha }_i与X_{it},{\epsilon }_{it}不相关$;$var(\epsilon )={\sigma }_{\epsilon }为常数$
推导：
$cov(v_{it},v_{is})=cov({\alpha }_i+{\epsilon }_{it},{\alpha }_i+{\epsilon }_{is})=cov({\alpha }_i,{\alpha }_i+{\epsilon }_{is})+cov({\epsilon }_{it},{\alpha }_i+{\epsilon }_{is})=cov({\alpha }_i,{\alpha }_i)+cov({\alpha }_i,{\epsilon }_{is})+cov({\epsilon }_{it},{\alpha }_i)+cov({\epsilon }_{it},{\epsilon }_{is})=\{\begin{array}{ll}{\sigma }_{\alpha }^2& \text{if }t\ne s\\ {\sigma }_{\alpha }^2+{\sigma }_{\epsilon }& \text{if }t=s\end{array}$
所以不满足古典假定，存在异方差与自相关问题。

估计方法展示

• 可行的广义最小二乘法(FGLS)
  
  
  

模型设定检验

F检验（chow’s test）

原假设：混合回归模型
备择假设：其他模型

以个体固定效应模型为例：$Y_{it}=u_i+X_{it}^{\prime }\beta +{\epsilon }_{it}$

原假设：$u_1=u_2=...=u_N$ （存在约束，截距不会变）
$Y_{it}=u_i+X_{it}^{\prime }\beta +{\epsilon }_{it}$
计算回归的$RS{S}_r$
备择假设：$u_1，u_2，...，u_N不全相等$ （无约束，截距会变）
$Y_{it}=u_i+X_{it}^{\prime }\beta +{\epsilon }_{it}$
计算回归的$RS{S}_u$

F统计量构造：
$F=\frac{(RS{S}_r-RS{S}_u)/[(NT-k-1)-(NT-k-N)]}{RS{S}_u/(NT-k-N)}\sim F(N-1,NT-k-N)$

项目	含义
$RS{S}_r$	有约束模型的残差平方和(混合模型，有约束)
$RS{S}_u$	无约束模型的残差平方和(变截距模型)
$k$	解释变量个数

LR检验

原假设：混合回归模型
备择假设：其他模型

以个体固定效应模型为例：$Y_{it}=u_i+X_{it}^{\prime }\beta +{\epsilon }_{it}$

原假设：$u_1=u_2=...=u_N$ （存在约束，截距不会变）
$Y_{it}=u_i+X_{it}^{\prime }\beta +{\epsilon }_{it}$
计算回归的最大似然函数值的对数$ln(L_r)$
备择假设：$u_1，u_2，...，u_N不全相等$ （无约束，截距会变）
$Y_{it}=u_i+X_{it}^{\prime }\beta +{\epsilon }_{it}$
计算回归的最大似然函数值的对数$ln(L_u)$

LR统计量构造：
$LR=-2(ln{L}_r-ln{L}_u)渐近服从{\chi }^2(约束条件的个数:N-1)$

豪斯曼检验（Hauseman’s test）

原假设：个体随机效应模型(个体效应与回归变量无关)
备择假设：个体固定效应模型(个体效应与回归变量有关)

检验的原理：
利用组内估计(within)，无论是随机效应模型的参数估计值还是固定效应模型的参数估计值，估计参数值都是一致的
利用广义最小二乘法，对随机效应模型的参数估计值是一致的，对于随机效应模型的参数估计值是不一致的

真实模型	组内估计${\hat{\beta }}_w$	广义最小二乘法$\widetilde{{\beta }_{re}}$
$随机效应模型$	一致估计量	非一致估计量
$固定效应模型$	一致估计量	一致估计量

检验逻辑图：

变截距面板数据模型建模步骤