【数据结构】图的总结——基本知识要点汇总

halo~我是bay_Tong桐小白
本文内容是桐小白个人对所学知识进行的总结和分享，知识点会不定期进行编辑更新和完善，了解最近更新内容可参看更新日志，欢迎各位大神留言、指点

【更新日志】

最近更新：

• 暂时没有编辑记录，后续会持续完善优化

计算机统考408考纲要求

2021计算机统考408考纲数据结构学科考察目标

• 掌握数据结构的基本概念、基本原理和基本方法
• 掌握数据结构的逻辑结构、存储结构及基本操作的实现，能够对算法进行基本的时间复杂度与空间复杂度的分析
• 能够运用数据结构的基本原理和方法进行问题的分析与求解，具备采用C或C++语言设计与实现算法的能力

2021计算机统考408数据结构考纲变动情况

2021计算机统考408考纲对图部分考察要求

图的相关基本概念

• 邻接点：边的两个顶点
• 关联边：若边e = ( v , u )，则称顶点v、u与边e关联
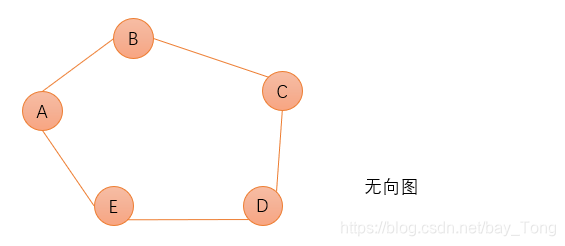
• 无向图：<x,y>∈VR且<y,x>∈VR，即(x,y)为无序对，图中的边无向
  
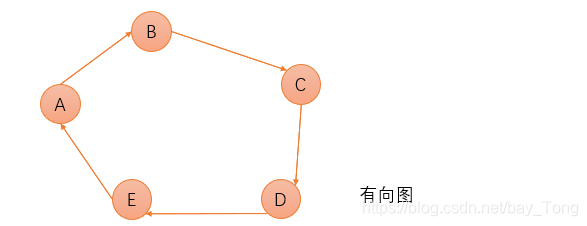
• 有向图：<x,y>表示从x到y有一条弧，x为弧尾，y为弧头，即图中的边有向
  
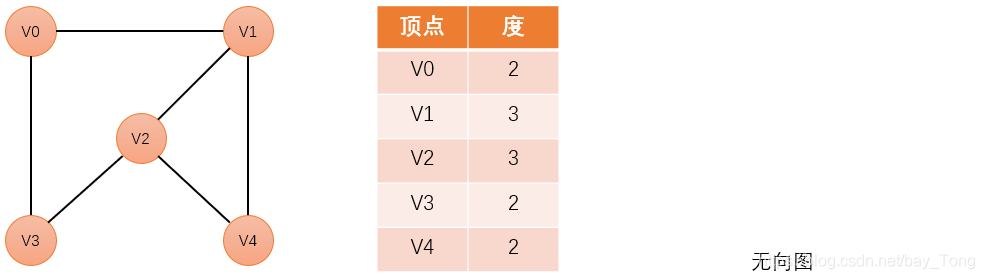
• 顶点的度
  无向图：顶点v的度 = 与v相关联的边的数目
  有向图：顶点v的度 = v的出度（以v为起点的有向边数） + v的入度（以v为终点的有向边数）
  
  
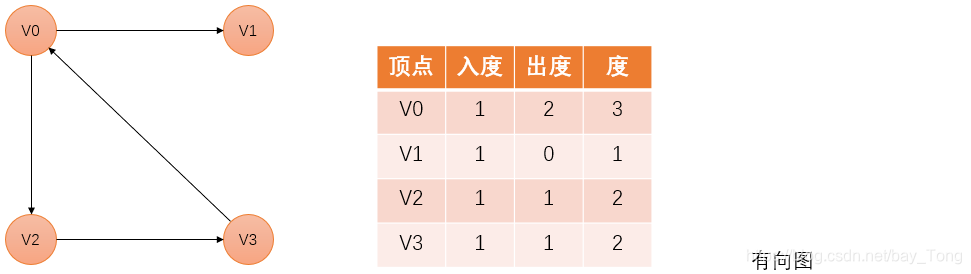
• 完全图：一个简单的无向图，其中每对不同的顶点之间都恰连有一条边相连
  无向完全图：含n个顶点的无向完全图，有n(n-1)/2条边
  有向完全图：含n个顶点的有向完全图，有n(n-1)条弧
• 连通图：无向图G中任一顶点均可到达其它任一顶点，即对任何两个顶点v、u，都存在从v到u的路径，则G为连通图
• 强连通图：有向图中任意两点都有路径
  要连通具有n个顶点的有向图，至少需要n条边
• 子图：
  
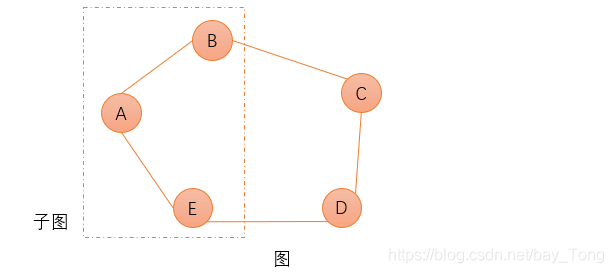
• 生成子图：
  1.包含图中所有顶点
  2.包含图中若干条边
• 生成树：
  1.包含图中所有顶点
  2.包含图中若干条边，通过这些边联通所有顶点且没有回路，即若图中v个顶点，则生成树包含全部的v个顶点，v-1条边连通所有顶点，无回路，且都在图中
  
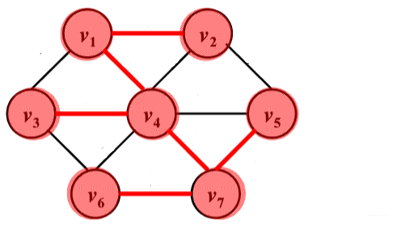
• 极小连通子图：一个连通图的生成树是原图的一个极小连通子图，它含有图中全部 n 个顶点，包含且只包含图中的 n-1 条边，即
  1.该子图是连通子图，包含原图的所有顶点
  2.子图中无回路，在该子图中删除任何一条边，子图不再连通
• 极大连通子图：对子图再增加原图中的其它顶点子图就不再连通
• 连通分量：无向图G的极大连通子图称为图G的连通分量。任何连通图的连通分量只有一个，即其自身。非连通图的无向图有多个连通分量
• 强连通分量：非强连通图的极大连通子图称为它的强连通分量

【PS：图中的边不考虑重边和自回路；图不可以是空图，图可以没有边，但是至少要有一个顶点】

图的存储结构

（图的存储也是广义表多重链表的一种应用，广义表工作原理详细见本栏文章《数组和广义表总结——基本知识要点汇总》）

邻接矩阵表示法

邻接矩阵：二维数组来表示，如G[ i ][ j ]表示 i 到 j 的一条边，无权图中若有边则G[ i ][ j ]的值为1否则为0，有权图中若有边则该值可以是边的权重，若无边则为无穷大，以一个很大的数来表示

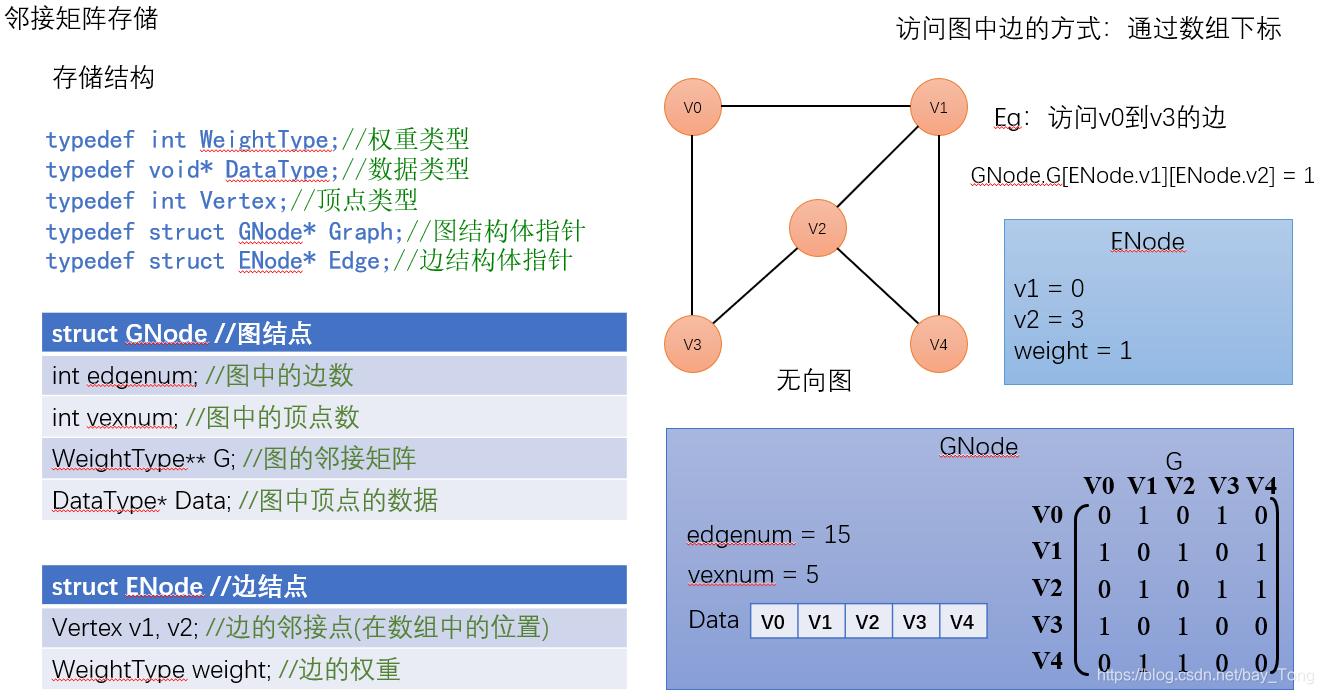
【无向图可以进行压缩存储，用一维数组只存矩阵的一半，通常习惯存下三角矩阵。邻接矩阵适合用于稠密图（此部分可与对称矩阵进行联系，对称矩阵详细内容见本栏文章《数组和广义表总结——基本知识要点汇总》）】

• 根据邻接矩阵求顶点v的度：遍历顶点v所在行，求1（或非无穷大）的个数，即为顶点v的出度
• 根据邻接矩阵找邻接点：即二维数组单元对应另一下标

邻接表表示法

邻接表：将一个顶点的所有出边邻接点构成一个单链表，该链表的头指针和该顶点数据一起存在一个结构数组中（类比树的孩子表示法，树的孩子表示法详细内容见本栏文章《树和二叉树总结——基本知识要点汇总》）

【邻接表适用于稀疏图，无向图邻接表中，设顶点有m个，图的边数为e，则使用邻接表存储占用存储空间为 m+2*e ，会造成一定程度的空间浪费】

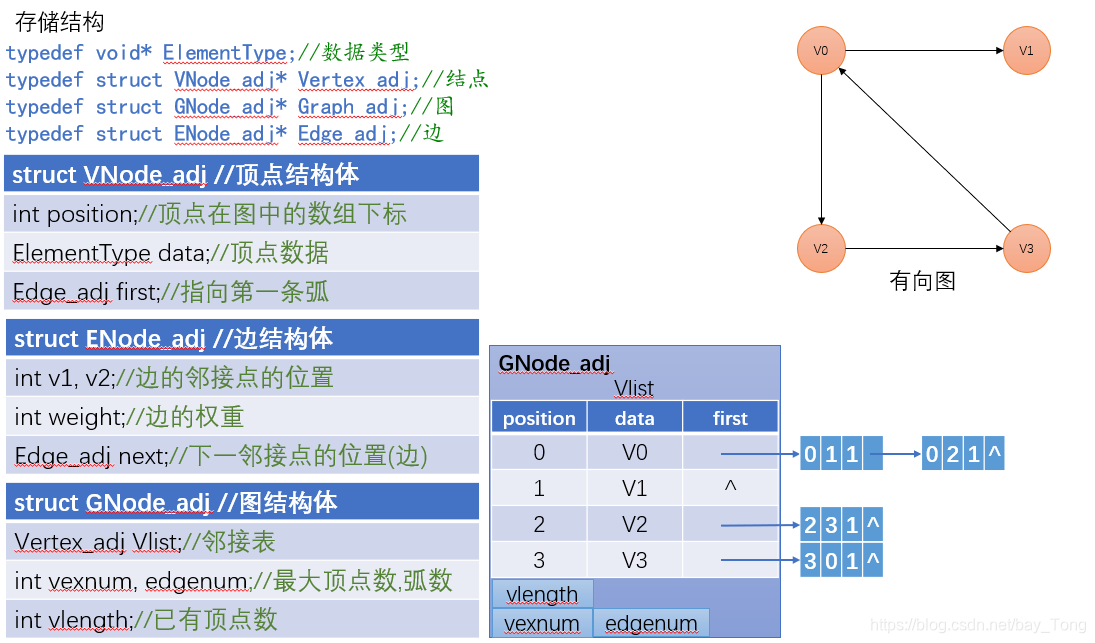
• 根据邻接表求顶点v的度：遍历顶点v的单链表，链表的长度即为顶点v的出度，求顶点的入度则需要遍历整个数组的所有邻接链表（无向图的入度等于出度，无需遍历所有邻接表）
• 根据邻接表找邻接点：链表结点中另一邻接点的值即为另一邻接点的下标

逆邻接表（入边表）：以同一顶点为终点的弧构成一个单链表，该链表的头指针和该顶点数据一起存储在一个结构数组中

图的十字链表法与邻接多重表后续更新……
图的十字链表部分内容可见本栏文章《数组和广义表总结——基本知识要点汇总》

图的遍历

从图的某顶点出发，访问图中所有顶点，并且每个顶点仅访问一次，主要遍历方法有两种，即深度优先遍历（DFS）与广度优先遍历（BFS）

深度优先遍历（DFS）

基本思路：

• 从图中某个未被访问过的顶点v出发，访问顶点v
• 若v有未被访问的邻接点，则访问该邻接点，并继续从该点出发，继续对图进行深度优先遍历，直至图中和v有路径相通的顶点均被访问
• 访问下一个未被访问过的顶点，进行深度优先遍历，直至图中所有顶点均被访问

根据深度优先遍历策略基本思路特点，可选择栈结构（暂存当前结点，访问其邻接点，实现路径相通的顶点遍历）进行算法的实现

详细代码实现见基本操作集汇总部分

广度优先遍历（BFS）

基本思路：

• 从图中某未访问过的顶点v出发，访问顶点v
• 访问v的所有未被访问的邻接点
• 依次从这些邻接点出发，访问它们的所有未被访问的邻接点，直到图中所有访问过的顶点的邻接点都被访问

根据广度优先遍历策略基本思路特点，可选择队列结构（暂存当前顶点的邻接点，顺序访问所有邻接点）进行算法的实现

详细代码实现见基本操作集汇总部分

图的连通性问题

• 连通图仅调用一次搜索过程便可以遍历图中的各个顶点
• 非连通图需多次调用搜索过程，每次调用得到的顶点访问序列恰为各连通分量中的顶点集
• 通过遍历得到的为深度优先生成树与广度优先生成树
  （1）深度优先生成树：
  
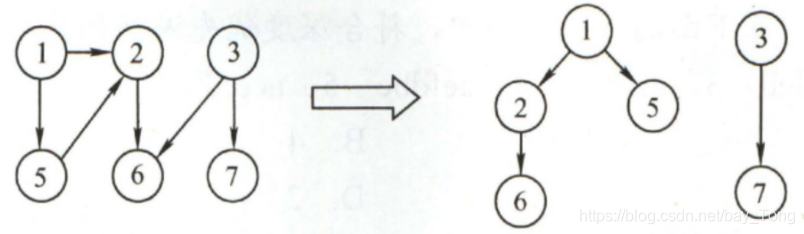
  （2）广度优先生成树：
  
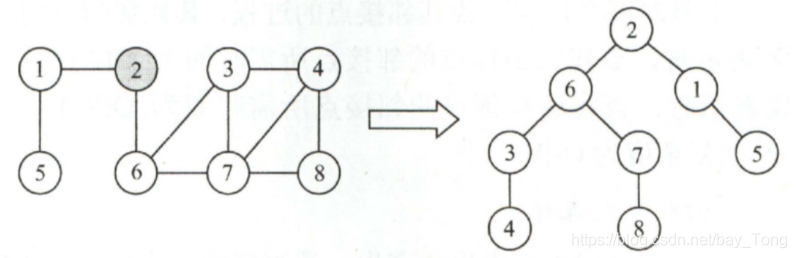
• 对于非连通图，每个连通分量的顶点集和走过的边即集一起构成若干生成树，称为生成森林

最小生成树（MST）

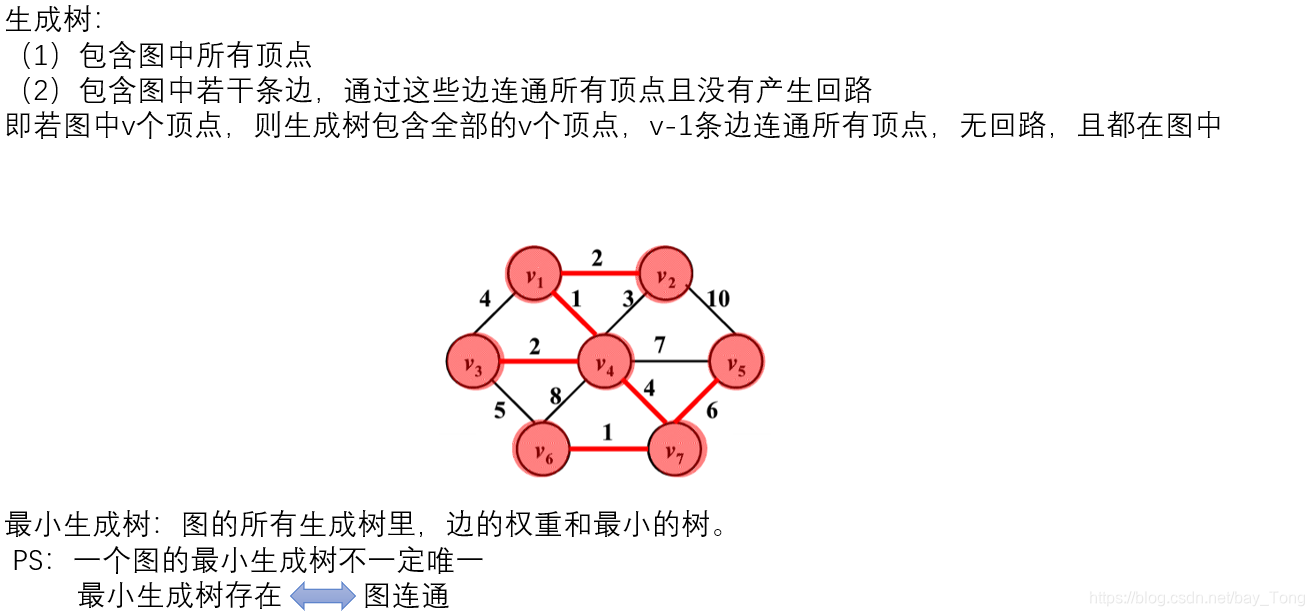
典型构造策略思想：贪心算法

Prim算法

初始化：向空树中添加图的任一顶点
之后循环（重复下列操作至所有顶点被添加）：从已添加顶点上选出权值最小的边，并把该边连接的顶点加入（添加顶点不能够重复）

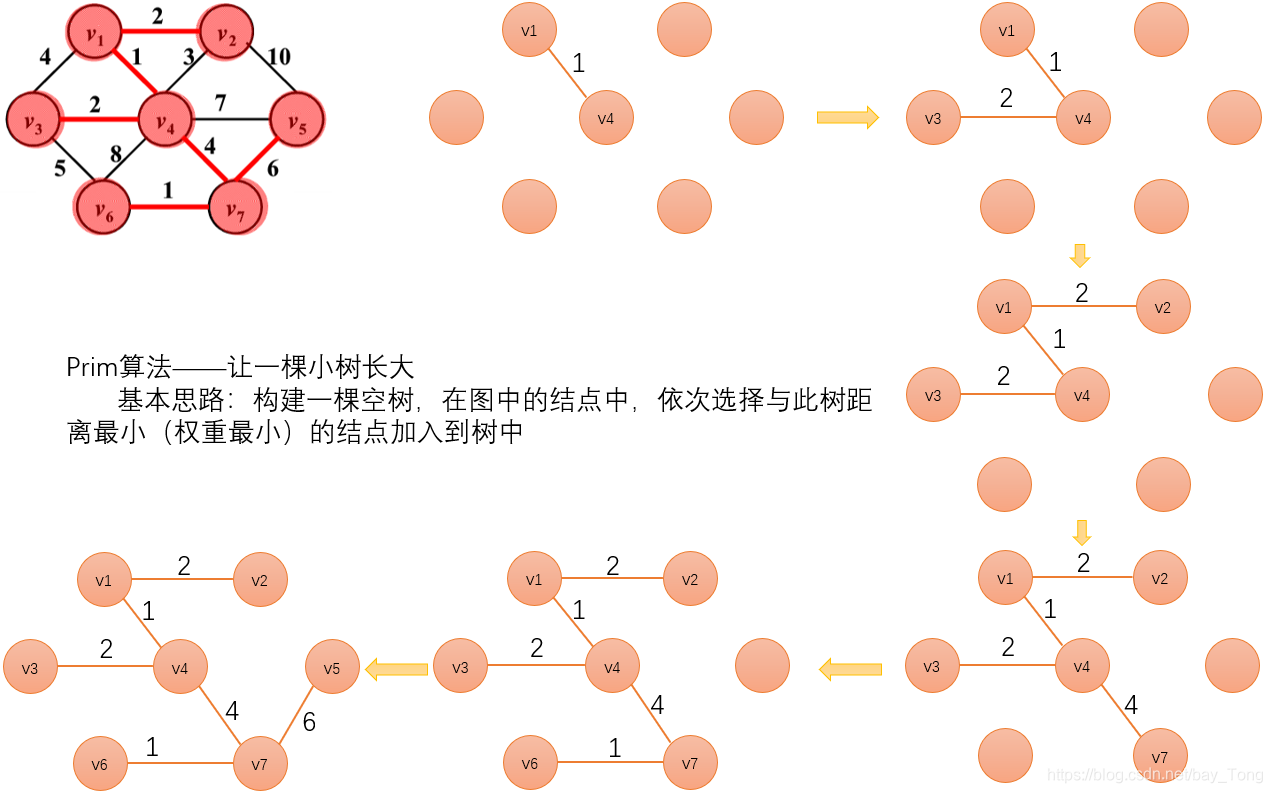
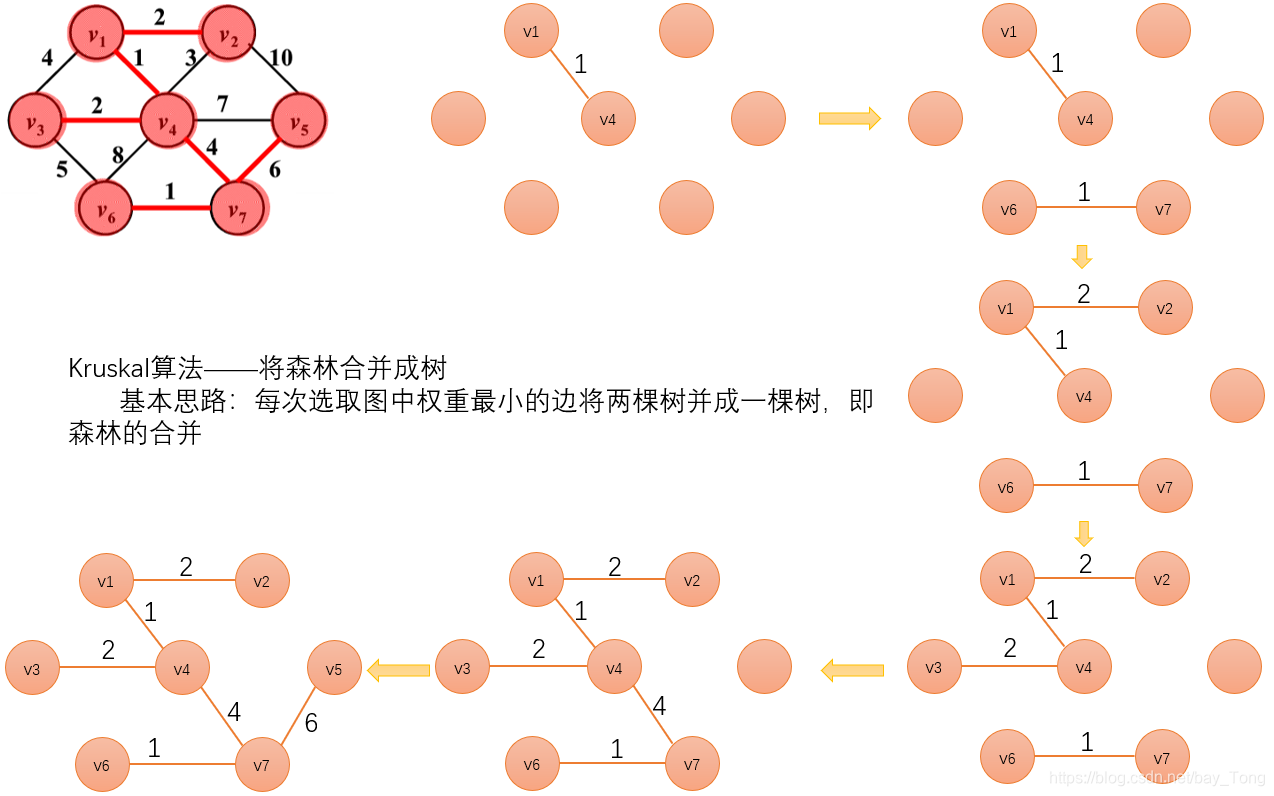
Kruskal算法

每次选取图中权重最小的边将两棵树并成一棵树，即森林的合并

最短路径问题

最短路径：

• 非带权图中：经过的边数最少；
• 带权图中：路径中的边权值之和最小

最短路径问题：

• 单源最短路径问题：给定图、给定一个顶点（源点）计算从源点到所有其它各顶点的最短路径长度
  ○ 思路：最短路径的子路径也是最短路径
  ○ 无权图的单元最短路算法：BFS算法
  ○ 有权图的单源最短路算法：Dijkstra算法
  从源点出发（设为集合S），每一次从其它顶点集合（U）中按最短路径长度递增的次序依次把U中顶点加入S中，直至全部顶点都加入到S中，算法结束
• 所有点对的最短路径问题：求所有顶点之间的最短路径和最短距离
  ○ 方法一：重复调用Dijkstra算法
  ○ 方法二：floyd算法（递归关系的建立，用一个矩阵存顶点到其它顶点的距离）

拓扑排序与关键路径

相关概念：

• DAG图：有向无环图
• AOV网：顶点表示活动，有向边表示活动先后关系
• 拓扑序列：设图G=(V,E)为有n个顶点的有向图，若从Vi到Vj有一条路径且有明确的先后顺序，则这条路径上的顶点序列V1，V2….为拓扑序列
• 拓扑排序：找到一个有向图的拓扑序列的过程
  （1）若AOV网中不存在回路，则所有活动可拍成一个线性序列，且有明确的先后关系（每个活动的所有前驱活动均在该活动之前），则该序列为拓扑序列
  （2）拓扑序列不唯一
  （3）AOV网不一定都有拓扑序列
  （4）拓扑序列的实际意义：按照拓扑序列中的顶点次序进行每一项活动，可保证整个工程顺利进行
• AOE网：顶点表示时间，弧表示活动，弧的权值表示活动所需要的时间

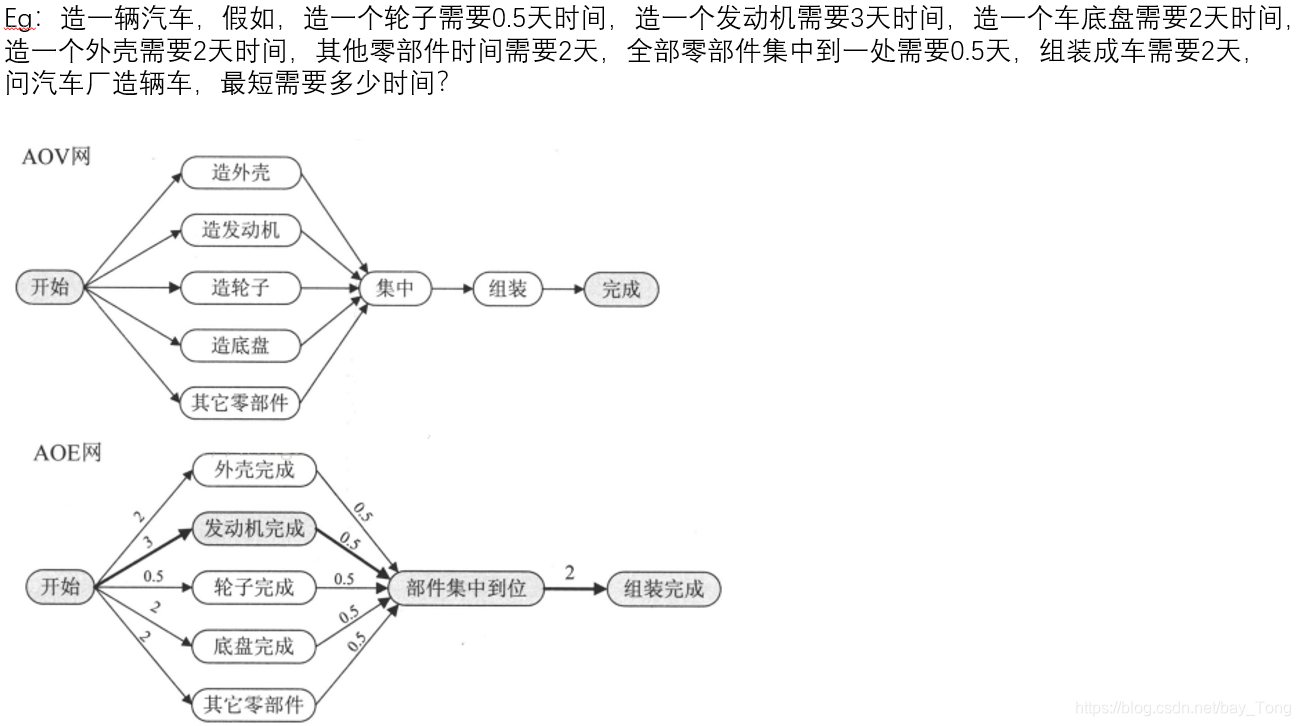
求拓扑排序思路：

• 在AOV网中选一个没有直接前驱的顶点并输出
• 从图中删去该顶点同时删去所有它发出的有向边
• 重复以上步骤
  （1）若全部顶点均已输出则拓扑排序完成
  （2）若图中还有未输出的顶点但已跳出处理循环，则AOV网中必定存在有向环，无法得到拓扑序列

关键路径：从源点到汇点的最长路径的长度，即完成整个工程任务所需的时间

关键活动：关键路径上的活动

求关键路径：松弛时间（时间余量）为0的活动为关键活动

• 对图中顶点进行拓扑排序，排序过程中求出每个事件的最早发生时间
• 按逆拓扑序列求每个事件的最晚发生时间
• 最早开始时间和最晚发生时间相同的活动即为关键活动

基本操作集汇总（代码实现）

【此部分是为将理论进行实践检验理论知识理解程度而进行的C语言代码实现汇总，在C++语言中的STL标准模板库有专门的头文件、数据结构及相关函数操作集的集成可直接进行调用】
【为了方便调用，采用多文件编程方式，代码已基本完成，实际使用时依据题目实际情况进行直接调用或简单修改后调用，算法的健壮性有待进一步测试，后续会持续对代码进行完善和优化】
【此部分的遍历等操作会用到栈结构与队列结构，栈与队列的基本工作原理及其基本操作集等详细见本栏文章《栈和队列总结——基本知识要点汇总》】

图的邻接矩阵存储基本操作集（C语言实现）

Graph.h文件

#pragma once
#ifndef GRAPH
#define GRAPH

#define false 0
#define true 1
#define INF_MAX 65533
#define ERROR -1
/*邻接矩阵法*/
typedef int WeightType;//权重类型
typedef int DataType;//数据类型
typedef int Vertex;//顶点类型
typedef struct GNode* Graph;//图结构体
typedef struct ENode* Edge;//边结构体
struct GNode {
    
    
	//int vexnum;
	int edgenum;
	int maxVexnum;
	WeightType** G;
	DataType* Data;
};
struct ENode {
    
    
	Vertex v1, v2;
	WeightType weight;
};
extern int* visit;

Graph CreateGraph(int maxVexnum);//建立初始图
void InsertEdge(Graph G, Edge e);//插入弧
Graph BuildGraph();//构建完整图
void DFSTravers(Graph G);//深度遍历
void DFS(Graph G, Vertex v);//深度遍历递归子程序
void BFS(Graph G);//广度遍历
int nodeDegree(Graph G, Vertex v);//求结点的度
void findConnect(Graph G, Vertex v);//就结点的邻接点
void ShortestPath(Graph G, Vertex v, int Dist[]);//计算G中顶点v到其它点的最短距离
void MST_Prim(Graph G);//最小生成树

#endif // !GRAPH

Graph.c文件

#include"Graph.h"
#include"Queue.h"
#include<stdio.h>
#include<stdlib.h>
#include<memory.h>

int* visit;
//建立初始图
Graph CreateGraph(int maxVexnum) {
    
    
	int i = 0, j = 0;
	Graph G = (Graph)calloc(1, sizeof(struct GNode));
	if (!G) {
    
     perror("error\n"); exit(1); }
	if (maxVexnum <= 0) {
    
     printf("输入有误\n"); free(G); return; }
	G->maxVexnum = maxVexnum;
	G->Data = (DataType*)calloc(maxVexnum, sizeof(DataType));
	G->G = (WeightType**)calloc(maxVexnum, sizeof(WeightType*));
	if (!G->Data || !G->G) {
    
     perror("error\n"); exit(1); }
	for (i = 0; i < maxVexnum; i++) {
    
    
		G->G[i] = (WeightType*)calloc(maxVexnum, sizeof(WeightType));
		if(!G->G[i]){
    
     perror("error\n"); exit(1); }
		for (j = 0; j < maxVexnum; j++) {
    
    
			G->G[i][j] = INF_MAX;
		}
	}
	return G;
}
//插入结点
//void InsertVertex(Graph G, Vertex v) {
    
    

//}
//插入弧
void InsertEdge(Graph G, Edge e) {
    
    
	if (e->v1 >= 0 && e->v1 < G->maxVexnum&&e->v2 >= 0 && e->v2 < G->maxVexnum) {
    
    
		G->G[e->v1][e->v2] = e->weight;
		/*若为无向图*/
		G->G[e->v2][e->v1] = e->weight;
	}
	else {
    
     printf("Insert_error\n"); return; }
}
//构建完整图
Graph BuildGraph() {
    
    
	int i = 0;
	int maxVexnum = 0;
	Graph G;
	Edge E;
	printf("输入要创建的图中顶点最大个数：");
	scanf("%d", &maxVexnum);
	G = CreateGraph(maxVexnum);
	for (i = 0; i < maxVexnum; i++) {
    
    
		printf("输入顶点的data：");
		scanf("%d", &G->Data[i]); fflush(stdin);
	}
	printf("输入要创建的图中边的条数：");
	scanf("%d", &G->edgenum);
	if (G->edgenum > 0) {
    
    
		E = (Edge)calloc(1, sizeof(struct ENode));
		if (!E) {
    
     perror("error\n"); exit(1); }
		for (i = 0; i < G->edgenum; i++) {
    
    
			printf("输入边的两个邻接点以及边的权重：");
			scanf("%d%d%d", &E->v1, &E->v2, &E->weight); fflush(stdin);
			InsertEdge(G, E);
		}
		free(E);
	}
	else if (G->edgenum < 0) {
    
    
		printf("Input_error\n");
		free(G->Data); 
		for (i = 0; i < G->maxVexnum; i++) {
    
    	free(G->G[i]);	}
		free(G); return NULL;
	}
	return G;
}
//深度遍历
void DFSTravers(Graph G) {
    
    
	Vertex v = 0;
	visit = (int*)calloc(G->maxVexnum, sizeof(int));
	if (!visit) {
    
     perror("error\n"); exit(1); }
	for (v = 0; v < G->maxVexnum; v++) {
    
    	DFS(G, v);	}
	free(visit);
}
//深度遍历递归子程序
void DFS(Graph G, Vertex v) {
    
    
	Vertex i;
	if (visit[v] == false) {
    
    
		visit[v] = true;
		printf(" %d", G->Data[v]);
	}
	for (i = 0; i < G->maxVexnum; i++) {
    
    
		if (G->G[v][i] != INF_MAX) {
    
    
			if (visit[i] == false) {
    
    
				DFS(G, i);
			}
		}
	}
}
//广度遍历
void BFS(Graph G) {
    
    
	Vertex v = 0, i = 0;
	Queue Q = CreateQueue(G->maxVexnum);
	visit = (int*)calloc(G->maxVexnum, sizeof(int));
	if (!visit) {
    
     perror("error\n"); exit(1); }
	for (v = 0; v < G->maxVexnum; v++) {
    
    
		if (visit[v] == false) {
    
    
			visit[v] = true;	printf(" %d", G->Data[v]);
			AddQ(Q, v);
			if (!IsEmptyQ(Q)) {
    
    
				v = DeleteQ(Q);
				for (i = 0; i < G->maxVexnum; i++) {
    
    
					if (G->G[v][i] != INF_MAX) {
    
    
						if (visit[i] == false) {
    
    
							visit[i] = true;	printf(" %d", G->Data[i]);
							AddQ(Q, i);
						}
					}
				}
			}	
		}
	}
	free(visit);
	free(Q);
}
//求结点的度
int nodeDegree(Graph G, Vertex v) {
    
    
	Vertex i = 0;
	int degree = 0;
	if (v < 0 || v >= G->maxVexnum) {
    
     printf("Find_error\n"); return ERROR; }
	for (i = 0; i < G->maxVexnum; i++) {
    
    
		if (G->G[v][i] != INF_MAX) {
    
    
			degree++;
		}
		if (G->G[i][v] != INF_MAX) {
    
    
			degree++;
		}
	}
	return degree;
}
//就结点的邻接点
void findConnect(Graph G, Vertex v) {
    
    
	if (v < 0 || v >= G->maxVexnum) {
    
     printf("Find_error\n"); return; }
	Vertex i = 0;
	visit = (int*)calloc(G->maxVexnum, sizeof(int));
	if (!visit) {
    
     perror("error\n"); exit(1); }
	for (i = 0; i < G->maxVexnum; i++) {
    
    
		if (G->G[v][i] != INF_MAX) {
    
    
			printf(" %d", G->Data[i]);
			visit[i] = true;
		}
		if (G->G[i][v] != INF_MAX && visit[i] == false) {
    
    
			printf(" %d", G->Data[i]);
		}
	}
	free(visit);
}
//计算G中顶点v到其它点的最短距离，待完善……
void ShortestPath(Graph G, Vertex v, int Dist[]) {
    
    }
//最小生成树，待完善……
void MST_Prim(Graph G) {
    
    }

图的邻接表存储基本操作集（C语言实现）

Graph_adj.h文件

#pragma once
#ifndef GRAPH_ADJ
#define GRAPH_ADJ
#define true 1
#define false 0
#define ERROR -1

typedef void* ElementType;
typedef struct VNode_adj* Vertex_adj;//结点
typedef struct GNode_adj* Graph_adj;//图
typedef struct ENode_adj* Edge_adj;//边
/*邻接表法*/
struct VNode_adj {
    
    
	int position;//数组下标
	ElementType data;//顶点数据
	Edge_adj first;//指向第一条弧
};

struct ENode_adj {
    
    
	int v1, v2;//边的邻接点的位置
	int weight;//边的权重
	Edge_adj next;//下一邻接点
};

struct GNode_adj {
    
    
	Vertex_adj Vlist;//邻接表
	int vexnum, edgenum;//顶点数、弧数
	int vlength;
};
extern int* visit;

Graph_adj CreateGraph_adj(int vexnum);//建立初始图
void InsertVertex_adj(Graph_adj G, Vertex_adj v);//插入结点
void InsertEdge_adj(Graph_adj G, Edge_adj e);//插入弧
Graph_adj BuildGraph_adj();//构建完整图
void DFSTravers_adj(Graph_adj G);//深度遍历
void DFS_adj(Graph_adj G, Vertex_adj V);//深度遍历递归子程序
void BFS_adj(Graph_adj G);//广度遍历
int nodeDegree_adj(Graph_adj G, Vertex_adj v);//求结点的度
void findConnect_adj(Graph_adj G, Vertex_adj v);//求结点的邻接点
void ShortestPath_addj(Graph_adj G, Vertex_adj v, int Dist[]);//计算G中顶点v到其它点的最短距离
void MST_adj(Graph_adj G);//最小生成树


#endif // !GRAPH_ADJ

Graph_adj.c文件

#include"Graph_adj.h"
#include"Queue.h"
#include<stdio.h>
#include<stdlib.h>
#include<memory.h>

int* visit;
//建立初始图
Graph_adj CreateGraph_adj(int maxVexnum) {
    
    
	Graph_adj G = (Graph_adj)calloc(1, sizeof(struct GNode_adj));
	if (!G) {
    
     perror("error\n"); exit(1); }//建立图
	if (maxVexnum <= 0) {
    
     printf("输入有误\n"); free(G); return; }
	G->vexnum = maxVexnum;
	G->Vlist = (Vertex_adj)calloc(G->vexnum, sizeof(struct VNode_adj));
	if (!(G->Vlist)) {
    
     perror("error\n"); exit(1); }
	return G;
}
//插入顶点
void InsertVertex_adj(Graph_adj G, Vertex_adj v) {
    
    
	if (G->vlength >= G->vexnum) {
    
    
		printf("图满\n"); return;
	}
	(G->Vlist[G->vlength]).data = v->data;
	(G->Vlist[G->vlength]).first = v->first;
	(G->Vlist[G->vlength]).position = v->position;
	(G->vlength)++;
}
//插入弧
void InsertEdge_adj(Graph_adj G, Edge_adj e) {
    
    
	//判断改弧的两个邻接点是否在图中
	if (e->v1 >= 0 && e->v1 < G->vexnum&&e->v2 >= 0 && e->v2 < G->vexnum) {
    
    
		//新建一个弧结点备份
		Edge_adj newNode01 = (calloc)(1, sizeof(struct ENode_adj));
		if (!newNode01) {
    
     perror("error\n"); exit(1); }
		newNode01->v1 = e->v1;
		newNode01->v2 = e->v2;
		newNode01->weight = e->weight;
		//将其插入到图中相应位置
		newNode01->next = (G->Vlist[e->v1]).first;
		(G->Vlist[e->v1]).first = newNode01;
		//若为无向图则重复上述插入过程，仅改变v1v2位置
		Edge_adj newNode02 = (calloc)(1, sizeof(struct ENode_adj));
		if (!newNode02) {
    
     perror("error\n"); exit(1); }
		newNode02->v1 = e->v2;
		newNode02->v2 = e->v1;
		newNode02->weight = e->weight;
		//将其插入到图中相应位置
		newNode02->next = (G->Vlist[e->v2]).first;
		(G->Vlist[e->v2]).first = newNode02;
	}
	else {
    
     printf("Insert_Error\n"); return; }
}
//构建完整图
Graph_adj BuildGraph_adj() {
    
    
	int vexnum = 0;
	int i = 0;
	Graph_adj G;
	Edge_adj E;
	Vertex_adj v = (Vertex_adj)calloc(1, sizeof(struct VNode_adj));
	if (!v) {
    
     perror("error\n"); exit(1); }
	printf("输入要创建的图中结点数：");
	scanf("%d", &vexnum); fflush(stdin);
	G = CreateGraph_adj(vexnum);
	for (i = 0; i < G->vexnum; i++) {
    
    
		printf("输入要创建的图中结点的数据：");
		scanf("%d", &v->data); fflush(stdin);
		v->first = NULL;
		v->position = i;
		InsertVertex_adj(G, v);
	}
	printf("输入要创建的图中边数：");
	scanf("%d", &G->edgenum); fflush(stdin);
	if (G->edgenum > 0) {
    
    
		for (i = 0; i < G->edgenum; i++) {
    
    
			E = (Edge_adj)calloc(1, sizeof(struct ENode_adj));
			if (!E) {
    
     perror("error\n"); exit(1); }
			E->next = NULL;
			printf("依次输入该边的两个邻接点、weight：");
			scanf("%d%d%d", &(E->v1), &(E->v2), &(E->weight)); fflush(stdin);
			//E->v1--; E->v2--;
			InsertEdge_adj(G, E);
		}
		free(E);
	}
	if (G->edgenum < 0) {
    
    
		printf("输入有误\n");
		free(G); free(G->Vlist);
		return NULL;
	}
	return G;
}

//深度遍历
void DFSTravers_adj(Graph_adj G) {
    
    
	int i = 0;
	visit = (int*)calloc(G->vexnum, sizeof(int));
	if (!visit) {
    
     perror("error\n"); exit(1); }
	for (i = 0; i < G->vexnum; i++) {
    
    	DFS_adj(G, &G->Vlist[i]);	}
	free(visit);
}

//深度遍历递归子程序
void DFS_adj(Graph_adj G,Vertex_adj v) {
    
    
	Edge_adj E = v->first;
	if (visit[v->position] == false) {
    
    
		visit[v->position] = true;
		printf(" %d", v->data);
	}
	while (E) {
    
    
		if (visit[E->v2] == false) {
    
    
			DFS_adj(G, &G->Vlist[E->v2]);
		}
		E = E->next;
	}
}
//广度遍历
void BFS_adj(Graph_adj G) {
    
    
	visit = (int*)calloc(G->vexnum, sizeof(int));
	if (!visit) {
    
     perror("error\n"); exit(1); }
	Queue Q = CreateQueue(G->edgenum * 2);
	Vertex_adj V;
	Edge_adj E;
	int i = 0;
	for (i = 0; i < G->vexnum; i++) {
    
    
		if (visit[i] == false) {
    
    
			visit[i] = true;	printf(" %d", G->Vlist[i].data);
			AddQ(Q, &G->Vlist[i]);
		}
		if (!IsEmptyQ(Q)) {
    
    
			V = DeleteQ(Q);
			E = V->first;
			while (E) {
    
    
				if (visit[E->v2] == false) {
    
    
					visit[E->v2] = true;	printf(" %d", G->Vlist[E->v2].data);
					AddQ(Q, &G->Vlist[E->v2]);
				}
				E = E->next;
			}
		}
	}
	free(visit);
	free(Q);
}
//求结点的度
int nodeDegree_adj(Graph_adj G, Vertex_adj v) {
    
    
	if (v < 0 || v >= G->vexnum) {
    
     printf("Find_error\n"); return ERROR; }
	Edge_adj E;
	int i = 0;
	int degree = 0;
	for (i = 0; i < G->vexnum; i++) {
    
    
		E = G->Vlist[i].first;
		while (E) {
    
    
			if (E->v1 == v || E->v2 == v) {
    
    
				degree++;
			}
			E = E->next;
		}
	}
	return degree;
}
//就结点的邻接点
void findConnect_adj(Graph_adj G, Vertex_adj v) {
    
    
	if (v < 0 || v >= G->vexnum) {
    
     printf("Find_error\n"); return ERROR; }
	Edge_adj E;
	int i = 0;
	visit = (int*)calloc(G->vexnum, sizeof(int));
	if (!visit) {
    
     perror("error\n"); exit(1); }
	for (i = 0; i < G->vexnum; i++) {
    
    
		E = G->Vlist[i].first;
		while (E) {
    
    
			if (E->v1 == v || E->v2 == v) {
    
    
				if (visit[E->v2] == false && E->v2 != v) {
    
    
					visit[E->v2] = true;
					printf(" %d", G->Vlist[E->v2].data);
				}
				if (E->v2 == v) {
    
     break; }
			}
			E = E->next;
		}
	}
	free(visit);
}
//计算G中顶点v到其它点的最短距离，待完善……
void ShortestPath_adj(Graph_adj G, Vertex_adj v, int Dist[]) {
    
    }
//最小生成树，待完善……
void MST_adj(Graph_adj G) {
    
    }

持续更新中……
我是桐小白，一个摸爬滚打的计算机小白