XGBoost: A Scalable Tree Boosting System
Complete Guide to Parameter Tuning in XGBoost with codes in Python
Can Gradient Boosting Learn Simple Arithmetic?
【机器学习】决策树(下)——XGBoost、LightGBM(非常详细)
在GBDT损失函数 L ( y , f t − 1 ( x ) + h t ( x ) ) L\left(y, f_{t-1}(x)+h_{t}(x)\right) L(y,ft−1(x)+ht(x))的基础上,我们加入正则化项如下:
Ω ( h t ) = γ J + λ 2 ∑ j = 1 J w t j 2 \Omega\left(h_{t}\right)=\gamma J+\frac{\lambda}{2} \sum_{j=1}^{J} w_{t j}^{2} Ω(ht)=γJ+2λj=1∑Jwtj2
这里的 J J J是叶子节点的个数,而 w t j w_{tj} wtj是第 j j j个叶子节点的最优值。这里的 w t j w_{tj} wtj和我们GBDT里使用的 w t j w_{tj} wtj是一个意思,只是XGBoost的论文里用的是 w w w表示叶子区域的值,因此这里和论文保持一致。
最终XGBoost的损失函数可以表达为:
L t = ∑ i = 1 m L ( y i , f t − 1 ( x i ) + h t ( x i ) ) + γ J + λ 2 ∑ j = 1 J w t j 2 L_{t}=\sum_{i=1}^{m} L\left(y_{i}, f_{t-1}\left(x_{i}\right)+h_{t}\left(x_{i}\right)\right)+\gamma J+\frac{\lambda}{2} \sum_{j=1}^{J} w_{t j}^{2} Lt=i=1∑mL(yi,ft−1(xi)+ht(xi))+γJ+2λj=1∑Jwtj2
最终我们要极小化上面这个损失函数,得到第 t t t个决策树最优的所有 J J J个叶子节点区域和每个叶子节点区域的最优解 w t j w_{tj} wtj。XGBoost没有和GBDT一样去拟合泰勒展开式的一阶导数,而是期望直接基于损失函数的二阶泰勒展开式来求解。现在我们来看看这个损失函数的二阶泰勒展开式:
L t = ∑ i = 1 m L ( y i , f t − 1 ( x i ) + h t ( x i ) ) + γ J + λ 2 ∑ j = 1 J w t j 2 ≈ ∑ i = 1 m ( L ( y i , f t − 1 ( x i ) ) + ∂ L ( y i , f t − 1 ( x i ) ∂ f t − 1 ( x i ) h t ( x i ) + 1 2 ∂ 2 L ( y i , f t − 1 ( x i ) ∂ f t − 1 2 ( x i ) h t 2 ( x i ) ) + γ J + λ 2 ∑ j = 1 J w t j 2 \begin{aligned} L_{t} &=\sum_{i=1}^{m} L\left(y_{i}, f_{t-1}\left(x_{i}\right)+h_{t}\left(x_{i}\right)\right)+\gamma J+\frac{\lambda}{2} \sum_{j=1}^{J} w_{t j}^{2} \\ & \approx \sum_{i=1}^{m}\left(L\left(y_{i}, f_{t-1}\left(x_{i}\right)\right)+\frac{\partial L\left(y_{i}, f_{t-1}\left(x_{i}\right)\right.}{\partial f_{t-1}\left(x_{i}\right)} h_{t}\left(x_{i}\right)+\frac{1}{2} \frac{\partial^{2} L\left(y_{i}, f_{t-1}\left(x_{i}\right)\right.}{\partial f_{t-1}^{2}\left(x_{i}\right)} h_{t}^{2}\left(x_{i}\right)\right)+\gamma J+\frac{\lambda}{2} \sum_{j=1}^{J} w_{t j}^{2} \end{aligned} Lt=i=1∑mL(yi,ft−1(xi)+ht(xi))+γJ+2λj=1∑Jwtj2≈i=1∑m(L(yi,ft−1(xi))+∂ft−1(xi)∂L(yi,ft−1(xi)ht(xi)+21∂ft−12(xi)∂2L(yi,ft−1(xi)ht2(xi))+γJ+2λj=1∑Jwtj2
为了方便,我们把第 i i i个样本在第 t t t个弱学习器的一阶和二阶导数分别记为
g t i = ∂ L ( y i , f t − 1 ( x i ) ∂ f t − 1 ( x i ) , h t i = ∂ 2 L ( y i , f t − 1 ( x i ) ∂ f t − 1 2 ( x i ) g_{t i}=\frac{\partial L\left(y_{i}, f_{t-1}\left(x_{i}\right)\right.}{\partial f_{t-1}\left(x_{i}\right)}, h_{t i}=\frac{\partial^{2} L\left(y_{i}, f_{t-1}\left(x_{i}\right)\right.}{\partial f_{t-1}^{2}\left(x_{i}\right)} gti=∂ft−1(xi)∂L(yi,ft−1(xi),hti=∂ft−12(xi)∂2L(yi,ft−1(xi)
则我们的损失函数现在可以表达为:
L t ≈ ∑ i = 1 m ( L ( y i , f t − 1 ( x i ) ) + g t i h t ( x i ) + 1 2 h t i h t 2 ( x i ) ) + γ J + λ 2 ∑ j = 1 J w t j 2 L_{t} \approx \sum_{i=1}^{m}\left(L\left(y_{i}, f_{t-1}\left(x_{i}\right)\right)+g_{t i} h_{t}\left(x_{i}\right)+\frac{1}{2} h_{t i} h_{t}^{2}\left(x_{i}\right)\right)+\gamma J+\frac{\lambda}{2} \sum_{j=1}^{J} w_{t j}^{2} Lt≈i=1∑m(L(yi,ft−1(xi))+gtiht(xi)+21htiht2(xi))+γJ+2λj=1∑Jwtj2
损失函数里面 L ( y i , f t − 1 ( x i ) L(y_{i}, f_{t-1}(x_{i}) L(yi,ft−1(xi)是常数,对最小化无影响,可以去掉,同时由于每个决策树的第j个叶子节点的取值最终会是同一个值 w t j w_{tj} wtj,因此我们的损失函数可以继续化简。
L t ≈ ( ∑ i = 1 m g t i h t ( x i ) + 1 2 h t i h t 2 ( x i ) ) + γ J + λ 2 ∑ j = 1 J w t j 2 = ∑ j = 1 J ( ∑ x i ∈ R t j g t i w t j + 1 2 ∑ x i ∈ R t j h t i w t j 2 ) + γ J + λ 2 ∑ j = 1 J w t j 2 = ∑ j = 1 J [ ( ∑ x i ∈ R t j g t i ) w t j + 1 2 ( ∑ x i ∈ R t j h t i + λ ) w t j 2 ] + γ J \begin{aligned} L_{t} &\approx \left ( \sum_{i=1}^{m} g_{t i} h_{t}\left(x_{i}\right)+\frac{1}{2} h_{t i} h_{t}^{2}\left(x_{i}\right)\right)+\gamma J+\frac{\lambda}{2} \sum_{j=1}^{J} w_{t j}^{2} \\ &=\sum_{j=1}^{J}\left(\sum_{x_{i} \in R_{t j}} g_{t i} w_{t j}+\frac{1}{2} \sum_{x_{i} \in R_{t j}} h_{t i} w_{t j}^{2}\right)+\gamma J+\frac{\lambda}{2} \sum_{j=1}^{J} w_{t j}^{2} \\ &=\sum_{j=1}^{J}\left[\left(\sum_{x_{i} \in R_{t j}} g_{t i}\right) w_{t j}+\frac{1}{2}\left(\sum_{x_{i} \in R_{t j}} h_{t i}+\lambda\right) w_{t j}^{2}\right]+\gamma J \end{aligned} Lt≈(i=1∑mgtiht(xi)+21htiht2(xi))+γJ+2λj=1∑Jwtj2=j=1∑J⎝⎛xi∈Rtj∑gtiwtj+21xi∈Rtj∑htiwtj2⎠⎞+γJ+2λj=1∑Jwtj2=j=1∑J⎣⎡⎝⎛xi∈Rtj∑gti⎠⎞wtj+21⎝⎛xi∈Rtj∑hti+λ⎠⎞wtj2⎦⎤+γJ
我们把每个叶子节点区域样本的一阶和二阶导数的和单独表示如下:
G t j = ∑ x i ∈ R t j g t i , H t j = ∑ x i ∈ R t j h t i G_{t j}=\sum_{x_{i} \in R_{t j}} g_{t i}, H_{t j}=\sum_{x_{i} \in R_{t j}} h_{t i} Gtj=xi∈Rtj∑gti,Htj=xi∈Rtj∑hti
最终损失函数的形式可以表示为:
L t = ∑ j = 1 J [ G t j w t j + 1 2 ( H t j + λ ) w t j 2 ] + γ J L_{t}=\sum_{j=1}^{J}\left[G_{t j} w_{t j}+\frac{1}{2}\left(H_{t j}+\lambda\right) w_{t j}^{2}\right]+\gamma J Lt=j=1∑J[Gtjwtj+21(Htj+λ)wtj2]+γJ
现在我们得到了最终的损失函数,那么回到前面讲到的问题,我们如何一次求解出决策树最优的所有J个叶子节点区域和每个叶子节点区域的最优解 w t j w_{tj} wtj呢?
关于如何一次求解出决策树最优的所有 J J J个叶子节点区域和每个叶子节点区域的最优解 w t j w_{tj} wtj,我们可以把它拆分成2个问题:
- 如果我们已经求出了第 t t t个决策树的 J J J个最优的叶子节点区域,如何求出每个叶子节点区域的最优解 w t j w_{tj} wtj
- 对当前决策树做子树分裂决策时,应该如何选择哪个特征和特征值进行分裂,使最终我们的损失函数 L t L_t Lt最小?
对于第一个问题,其实是比较简单的,我们直接基于损失函数对 w t j w_{tj} wtj求导并令导数为0即可。这样我们得到叶子节点区域的最优解 w t j w_{tj} wtj表达式为:
w t j = − G t j H t j + λ w_{t j}=-\frac{G_{t j}}{H_{t j}+\lambda} wtj=−Htj+λGtj
这个叶子节点的表达式不是XGBoost首创,实际上在GBDT的分类算法里,已经在使用了。大家在梯度提升树(GBDT)原理小结第4.1节中叶子节点区域值的近似解表达式为:
c t j = ∑ x i ∈ R t j r t i / ∑ x i ∈ R t j ∣ r t i ∣ ( 1 − ∣ r t i ∣ ) c_{t j}=\sum_{x_{i} \in R_{t j}} r_{t i} / \sum_{x_{i} \in R_{t j}}\left|r_{t i}\right|\left(1-\left|r_{t i}\right|\right) ctj=xi∈Rtj∑rti/xi∈Rtj∑∣rti∣(1−∣rti∣)
它其实就是使用了上式来计算最终的 c t j c_{tj} ctj。注意到二元分类的损失函数是:
L ( y , f ( x ) ) = log ( 1 + exp ( − y f ( x ) ) ) L(y, f(x))=\log (1+\exp (-y f(x))) L(y,f(x))=log(1+exp(−yf(x)))
其每个样本的一阶导数为:
g i = − r i = − y i / ( 1 + exp ( y i f ( x i ) ) ) g_{i}=-r_{i}=-y_{i} /\left(1+\exp \left(y_{i} f\left(x_{i}\right)\right)\right) gi=−ri=−yi/(1+exp(yif(xi)))
其每个样本的二阶导数为:
h i = exp ( y i f ( x i ) ( 1 + exp ( y i f ( x i ) ) 2 = ∣ g i ∣ ( 1 − ∣ g i ∣ ) h_{i}=\frac{\exp \left(y_{i} f\left(x_{i}\right)\right.}{(1+\exp \left(y_{i} f\left(x_{i}\right)\right)^{2}}=\left|g_{i}\right|\left(1-\left|g_{i}\right|\right) hi=(1+exp(yif(xi))2exp(yif(xi)=∣gi∣(1−∣gi∣)
由于没有正则化项,则 c t j = − g i h i c_{t j}=-\frac{g_{i}}{h_{i}} ctj=−higi,即可得到GBDT二分类叶子节点区域的近似值。
现在我们回到XGBoost,我们已经解决了第一个问题。现在来看XGBoost优化拆分出的第二个问题:如何选择哪个特征和特征值进行分裂,使最终我们的损失函数 L t L_t Lt最小?
在GBDT里面,我们是直接拟合的CART回归树,所以树节点分裂使用的是均方误差。XGBoost这里不使用均方误差,而是使用贪心法,即每次分裂都期望最小化我们的损失函数的误差。
注意到在我们 w t j w_{tj} wtj取最优解的时候,原损失函数对应的表达式为:
L t = − 1 2 ∑ j = 1 J G t j 2 H t j + λ + γ J L_{t}=-\frac{1}{2} \sum_{j=1}^{J} \frac{G_{t j}^{2}}{H_{t j}+\lambda}+\gamma J Lt=−21j=1∑JHtj+λGtj2+γJ
如果我们每次做左右子树分裂时,可以最大程度的减少损失函数的损失就最好了。也就是说,假设当前节点左右子树的一阶二阶导数和为 G L G_L GL, H L H_L HL, G R G_R GR, H L H_L HL, 则我们期望最大化下式:
− 1 2 ( G L + G R ) 2 H L + H R + λ + γ J − ( − 1 2 G L 2 H L + λ − 1 2 G R 2 H R + λ + γ ( J + 1 ) ) -\frac{1}{2} \frac{\left(G_{L}+G_{R}\right)^{2}}{H_{L}+H_{R}+\lambda}+\gamma J-\left(-\frac{1}{2} \frac{G_{L}^{2}}{H_{L}+\lambda}-\frac{1}{2} \frac{G_{R}^{2}}{H_{R}+\lambda}+\gamma(J+1)\right) −21HL+HR+λ(GL+GR)2+γJ−(−21HL+λGL2−21HR+λGR2+γ(J+1))
整理下上式后,我们期望最大化的是:
max 1 2 G L 2 H L + λ + 1 2 G R 2 H R + λ − 1 2 ( G L + G R ) 2 H L + H R + λ − γ \max \frac{1}{2} \frac{G_{L}^{2}}{H_{L}+\lambda}+\frac{1}{2} \frac{G_{R}^{2}}{H_{R}+\lambda}-\frac{1}{2} \frac{\left(G_{L}+G_{R}\right)^{2}}{H_{L}+H_{R}+\lambda}-\gamma max21HL+λGL2+21HR+λGR2−21HL+HR+λ(GL+GR)2−γ
也就是说,我们的决策树分裂标准不再使用CART回归树的均方误差,而是上式了。
具体如何分裂呢?举个简单的年龄特征的例子如下,假设我们选择年龄这个 特征的值a作为决策树的分裂标准,则可以得到左子树2个人,右子树三个人,这样可以分别计算出左右子树的一阶和二阶导数和,进而求出最终的上式的值。
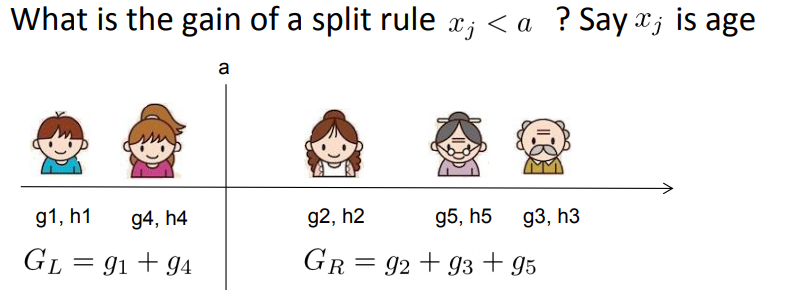
然后我们使用其他的不是值a的划分标准,可以得到其他组合的一阶和二阶导数和,进而求出上式的值。最终我们找出可以使上式最大的组合,以它对应的特征值来分裂子树。
至此,我们解决了XGBoost的2个优化子问题的求解方法。
XGBoost算法主流程
- (1) 计算第 i i i个样本 ( i = 1 , 2 , ⋯ m ) (i=1,2,\cdots m) (i=1,2,⋯m)在当前轮损失函数 L L L关于 f t − 1 ( x i ) f_{t-1}(x_i) ft−1(xi)的一阶导数 g t i g_{ti} gti,二阶导数 h t i h_{ti} hti,计算所有样本的一阶导数和 G t = ∑ i = 1 m g t i G_{t}=\sum_{i=1}^{m} g_{t i} Gt=∑i=1mgti,二阶导数和 H t = ∑ i = 1 m h t i H_{t}=\sum_{i=1}^{m} h_{t i} Ht=∑i=1mhti
- (2) 基于当前节点尝试分裂决策树,默认分数score=0,G和H为当前需要分裂的节点的一阶二阶导数之和。
- 对特征序号 k = 1 , 2 , ⋯ , K k=1,2,\cdots ,K k=1,2,⋯,K
- (a) G L = 0 , H L = 0 G_L=0, H_L=0 GL=0,HL=0
- (b.1) 将样本按特征 k k k从小到大排序,依次取出第 i i i个样本,依次计算当前样本放入左子树后,左右子树一阶和二阶导数和: G L = G L + g t i , G R = G − G L H L = H L + h t i , H R = H − H L \begin{aligned} G_{L} &=G_{L}+g_{t i}, G_{R}=G-G_{L} \\ H_{L} &=H_{L}+h_{t i}, H_{R}=H-H_{L} \end{aligned} GLHL=GL+gti,GR=G−GL=HL+hti,HR=H−HL
- (b.2) 尝试更新最大的分数: score = max ( score , 1 2 G L 2 H L + λ + 1 2 G R 2 H R + λ − 1 2 ( G L + G R ) 2 H L + H R + λ − γ ) \text { score }=\max \left(\text { score }, \frac{1}{2} \frac{G_{L}^{2}}{H_{L}+\lambda}+\frac{1}{2} \frac{G_{R}^{2}}{H_{R}+\lambda}-\frac{1}{2} \frac{\left(G_{L}+G_{R}\right)^{2}}{H_{L}+H_{R}+\lambda}-\gamma\right) score =max( score ,21HL+λGL2+21HR+λGR2−21HL+HR+λ(GL+GR)2−γ)
- (3) 基于最大score对应的划分特征和特征指分裂子树
- (4) 如果最大score为0,则当前决策树建立完毕,计算所有叶子区域的 w t j w_{tj} wtj, 得到弱学习器 h t ( x ) h_t(x) ht(x),更新强学习器 f t ( x ) f_t(x) ft(x),进入下一轮弱学习器迭代.如果最大score不是0,则转到第(2)步继续尝试分裂决策树。