建模算法整理:文章主要介绍了 差值算法。
参考学习资料:清风数学建模
其他资源:2016到2020美赛o奖论文=== 姜启源 司守奎电子书===论文模板 ====算法代码
如果需要可私信或者评论
文章目录
1 插值算法的作用
建模中,我们需要根据已知的函数点进行数据、模型的处理和分析,而有的时候现有的数据是极少的,不足以支撑分析的进行,这时就需要使用一些数学的方法,“模拟产生”一些新的但又比较靠谱的值来满足需求,这就是插值的作用。
2 插值和拟合区别
插值算法中,所得的多项式f(x)要经过所有的样本点。但是如果样本点太多,那么这个多项式次数过多,会造成龙格现象。
尽管我们可以选择分段的方法避免这种现象,但是更多时候我们更倾向于得到一个确定的曲线,尽管这个曲线不能过每一个样本店,但只要保证足够小即可,这就是拟合的思想。
3 插值和拟合的选取
当数据量不够,需要补充,且认定已有数据可信时,通常利用函数插值方法。
数据量多,不要求曲线经过每个点,同时要求多项式不要过于复杂我们选择拟合。
4 分段三次埃尔米特插值
4.1 代码实例
% 分段三次埃尔米特插值
x = -pi:pi; y = sin(x);
new_x = -pi:0.1:pi;
p = pchip(x,y,new_x);
plot(x, y, 'o', new_x, p, 'r-')
4.2 结果显示
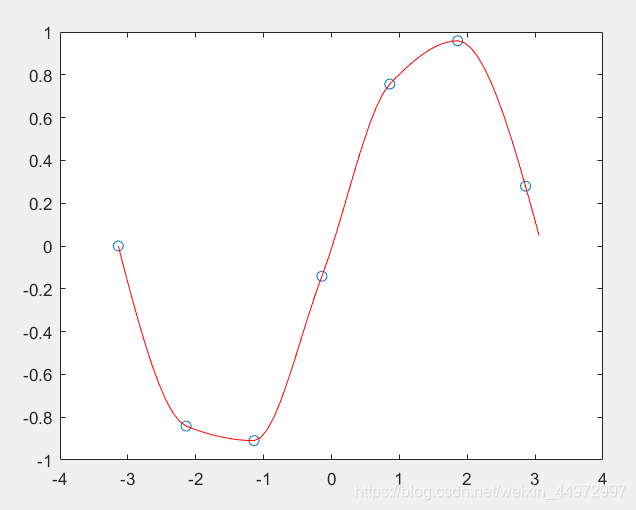
4.3 plot用法
% plot函数用法:
% plot(x1,y1,x2,y2)
% 线方式: - 实线 :点线 -. 虚点线 - - 波折线
% 点方式: . 圆点 +加号 * 星号 x x形 o 小圆
% 颜色: y黄; r红; g绿; b蓝; w白; k黑; m紫; c青
5 分段三次埃尔米特插值和三次样条插值的区别
5.1 代码实例
% 三次样条插值和分段三次埃尔米特插值的对比
x = -pi:pi;
y = sin(x);
new_x = -pi:0.1:pi;
p1 = pchip(x,y,new_x); %分段三次埃尔米特
p2 = spline(x,y,new_x); %三次样条插值
figure(2);
plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')
legend('样本点','三次埃尔米特插值','三次样条插值','Location','SouthEast')
% legend为标签 'Location','SouthEast'是为了设定显示位置
5.2 结果展示

5.3 原因解释
三次样条插值也是分段三次多项式插值,只需要被插值函数在插值节点处的函数值,不需要知道被插值函数在插值节点处的导数值,数据要求低,光滑性好,可以达到二阶导数连续。
三次分段Hermite插值是分段三次多项式插值,需要同时知道被插值函数在插值节点处的函数值和导数值,数据要求高,可以达到导数连续,光滑性不如样条插值的好.
6 n维数据差值(linear cubic spline)
6.1 代码实例
%格式 p = interpn(x1,x2,...,xn, y, new_x1,new_x2,...,new_xn, method)
% method是要插值的方法
%‘linear’:线性插值(默认算法);
%‘cubic’:三次插值;
%‘spline’:三次样条插值法;(最为精准) ‘nearest’:最邻近插值算法。
% n维数据的插值
x = -pi:pi; y = sin(x);
new_x = -pi:0.1:pi;
p = interpn (x, y, new_x, 'spline');
% 等价于 p = spline(x, y, new_x);
plot(x, y, 'o', new_x, p, 'r-')
6.2 结果显示
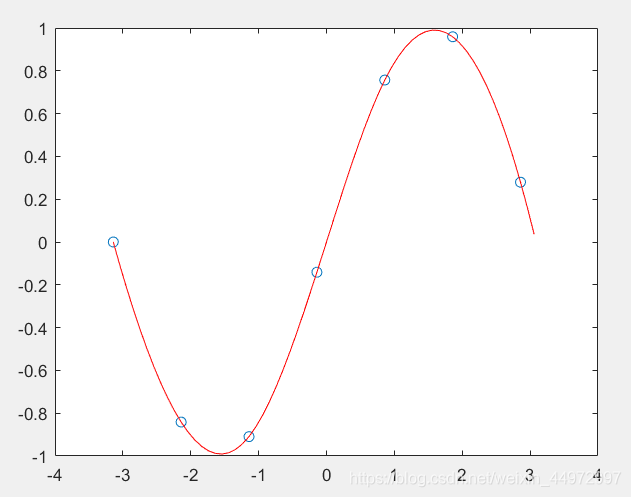
总结
文章纯属建模学习整理。
1、2016到2020美赛o奖论文
2、姜启源 司守奎电子书
3、论文模板
4、算法代码
如有需要上述资源可私信评论
最后希望给文章点个赞,整理不易!!!
最后希望给文章点个赞,整理不易!!!
最后希望给文章点个赞,整理不易!!!