交叉熵以及通过Python实现softmax_交叉熵（tensorflow验证）

交叉熵（Cross Entropy）

交叉熵（cross entropy）是深度学习中常用的一个概念，一般用来求目标与预测值之间的差距。

交叉熵（Cross Entropy）是Shannon信息论中一个重要概念，主要用于度量两个概率分布间的差异性信息。语言模型的性能通常用交叉熵和复杂度（perplexity）来衡量。交叉熵的意义是用该模型对文本识别的难度，或者从压缩的角度来看，每个词平均要用几个位来编码。复杂度的意义是用该模型表示这一文本平均的分支数，其倒数可视为每个词的平均概率。平滑是指对没观察到的N元组合赋予一个概率值，以保证词序列总能通过语言模型得到一个概率值。通常使用的平滑技术有图灵估计、删除插值平滑、Katz平滑和Kneser-Ney平滑。

信息论

在信息论中，交叉熵是表示两个概率分布p,q，其中p表示真实分布，q表示非真实分布，在相同的一组事件中，其中，用非真实分布q来表示某个事件发生所需要的平均比特数。从这个定义中，我们很难理解交叉熵的定义。下面举个例子来描述一下：

假设现在有一个样本集中两个概率分布p,q，其中p为真实分布，q为非真实分布。假如，按照真实分布p来衡量识别一个样本所需要的编码长度的期望为：

$$H(p)=\sum _{i}p(i)\cdot log(\frac{1}{p(i)})$$

但是，如果采用错误的分布q来表示来自真实分布p的平均编码长度，则应该是：

$$H(p,q)=\sum _{i}p(i)\cdot log(\frac{1}{q(i)})$$

此时就将$H(p,q)$称之为交叉熵。

交叉熵的计算方式如下：

对于离散变量采用以下的方式计算:$H(p,q)={\sum }_{x}p(x)\cdot log(\frac{1}{q(x)})$

对于连续变量采用以下的方式计算:${\int }_{X}P(X)log(Q(X))dr(x)=E_p[-logQ]$

相对熵

相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异。

维基百科中对相对熵的定义为：

In the context of machine learning, DKL(P‖Q) is often called the information gain achieved if P is used instead of Q.

即如果用P来描述目标问题，而不是用Q来描述目标问题，得到的信息增量。

在机器学习中，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]
直观的理解就是如果用P来描述样本，那么就非常完美。而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P。

KL散度的计算公式为：
$$D_{KL}(p||q)=\sum _{i=1}^{n}p(x_i)log(\frac{p(x_i)}{q(x_i)})\text{\hspace{1em}(1)}$$
其中$n$为事件的所有可能性。$D_{KL}$的值越小，表示$q$分布和$p$分布越接近。

交叉熵

交叉熵可在神经网络(机器学习)中作为损失函数，p表示真实标记的分布，q则为训练后的模型的预测标记分布，交叉熵损失函数可以衡量p与q的相似性。交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题，因为学习速率可以被输出的误差所控制。

在特征工程中，可以用来衡量两个随机变量之间的相似度。

在语言模型中（NLP）中，由于真实的分布p是未知的，在语言模型中，模型是通过训练集得到的，交叉熵就是衡量这个模型在测试集上的正确率。

对相对熵计算式(1)进行变形可以得到：
$$\begin{array}{rl}{D}_{KL}(p||q)& =\sum _{i=1}^{n}p(x_i)log(p(x_i))-\sum _{i=1}^{n}p(x_i)log(q(x_i))\\ & =-H(p(x))+[-\sum _{i=1}^{n}p(x_i)log(q(x_i))]\end{array}$$
等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵：
$$H(p,q)=-\sum _{i=1}^{n}p(x_i)log(q(x_i))$$

在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即$D_{KL}(y||\hat{y})$，由于KL散度中的前一部分$-H(y)$不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss，评估模型。

机器学习中的交叉熵

为什么要用交叉熵做损失函数？

在线性回归问题中，常常使用MSE（Mean Squared Error）作为loss函数，比如：
$$loss=\frac{1}{2m}\sum _{i=1}^m(y_i-\widehat{y_i}{)}^2$$
其中m表示样本数，loss为m个样本的loss均值。
MSE在线性回归问题中比较好用，那么在逻辑分类问题中还是如此么？

分类问题中的交叉熵

单类别是指，每一张图像样本只能有一个类别，比如只能是狗或只能是猫。

在单类别问题中，交叉熵的计算如下：

$$loss=-\sum _{i=1}^n{y}_{i}log(\widehat{y_i})$$

假设label和pred的取值如下：

	cat	dog	man
label	1	0	0
pred	0.7	0.2	0.1

计算可得：

$$Loss\_crossEntropy=-(1\times log(0.7)+0\times log(0.2)+0\times log(0.1))=-log(0.7)$$

同理可得batch_loss：
$$loss\_batch=-\frac{1}{m}\sum _{j=1}^m\sum _{i=1}^n{y}_{ji}log(\widehat{y_{ji}})$$

如果label为多分类，即类别不互斥的情况下，交叉熵的计算如下：
$$Loss\_crossEntropy=-ylog(\hat{y})-(1-y)log(1-\hat{y})$$
batch:
$$loss\_batch=\frac{1}{m}\sum _{j=1}^m\sum _{i=1}^n-y_{ji}log(\widehat{y_{ji}})-(1-y_{ji})log(1-\widehat{y_{ji}})$$

softmax

由于做交叉熵之前一般都会用进行softmax处理，所以这里简单介绍一下softmax。

假设我们有一个数组，V，Vi表示V中的第i个元素，那么这个元素的Softmax值就是

$$S_i=\frac{e^{V_i}}{{\sum }_j{e}^{V_j}}$$

也就是说，是该元素的指数，与所有元素指数和的比值。

softmax的过程如图所示：

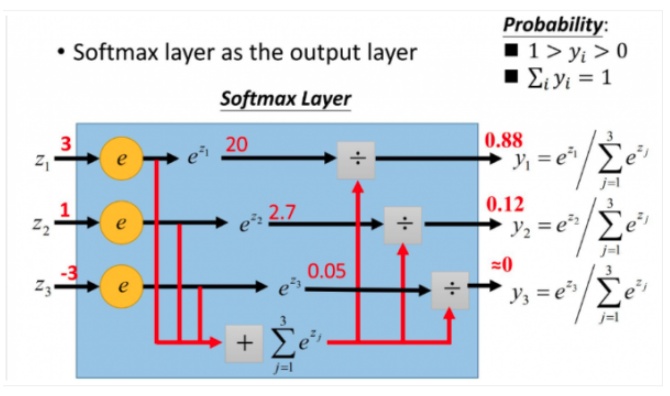
softmax直白来说就是将原来输出是3,1,-3通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标！

softmax_cross_entropy求导

在多分类问题中，我们经常使用交叉熵作为损失函数:
$$loss=-\sum _{i=1}^n{y}_{i}log(\widehat{y_i})$$
当预测第i个时，$y$可以认为是1，此时损失函数变成了：
$$los{s}_i=-log(\widehat{y_i})$$
接下来对Loss求导。根据定义：
$$y_i=\frac{e^i}{{\sum }_j{e}^j}$$
由于softmax已经将数值映射到了0-1之间，并且和为1，则有：
$$\frac{e^i}{{\sum }_j{e}^j}=1-\frac{{\sum }_{i\ne j}{e}^i}{{\sum }_j{e}^j}$$

下面是求导过程(结合链式法则)：
$$\begin{array}{rl}\frac{\partial los{s}_i}{{\partial }_i}& =-\frac{\partial ln{y}_i}{{\partial }_i}\\ & =-\frac{{\sum }_j{e}^j}{e^i}\frac{\partial }{{\partial }_i}(\frac{e^i}{{\sum }_j{e}^j})\\ & =-\frac{{\sum }_j{e}^j}{e^i}\frac{\partial }{{\partial }_i}(\frac{e^i}{{\sum }_{j\ne i}{e}^j+e^i})\\ & =-\frac{{\sum }_j{e}^j}{e^i}\frac{e^i{\sum }_j{e}^j-{e^i}^2}{({\sum }_{j\ne i}{e}^j+e^i{)}^2}\\ & =-\frac{{\sum }_j{e}^j-e^i}{{\sum }_j{e}^j}\\ & =-(1-\frac{e^i}{{\sum }_j{e}^j})\\ & =y_i-1\end{array}$$

Python实现单分类softmax_交叉熵

通过以上理论我们就可以自己实现交叉熵函数，并与流行框架中的计算结果进行对比

import numpy as np
import tensorflow as tf

# one-hot
def cross_entropy(y, y_hat):
    assert y.shape == y_hat.shape
    n = 1e-6
    res = -np.sum(np.nan_to_num(y * np.log(y_hat + n)), axis=1) # 行求和 
    return res

def softmax(y):
    y_shift = y - np.max(y, axis=1, keepdims=True)
    y_exp = np.exp(y_shift)
    y_exp_sum = np.sum(y_exp, axis=1, keepdims=True)
    return y_exp / y_exp_sum

if __name__ == "__main__":
    y_true = np.array([[1.0, 0.0, 0.0], [0.0, 0.8, 0.2]])
    y_pred = np.array([[4.0, 2.0, 1.0], [0.0, 5.0, 1.0]])
    y_pred_softmax = softmax(y_pred)
    
    print("my_softmax:\n", y_pred_softmax)
    print("tf_softmax:\n", tf.nn.softmax(logits=y_pred).numpy())
    
    my_loss = cross_entropy(y_true, y_pred_softmax)
    my_loss_meam = np.mean(my_loss)
    assert my_loss.shape == (2,)
    print("my_loss:\n", my_loss)
    print("my_loss_mean:\n", my_loss_meam)
    
    tf_loss = tf.nn.softmax_cross_entropy_with_logits(y_true, y_pred, axis=-1)  # one-hot
    tf_loss_meam = tf.reduce_mean(tf_loss)
    assert tf_loss.shape == (2,)
    print("tf_loss:\n", tf_loss.numpy())
    print("tf_loss_mean:\n", tf_loss_meam.numpy())

my_softmax:
 [[0.84379473 0.1141952  0.04201007]
 [0.00657326 0.97555875 0.01786798]]
tf_softmax:
 [[0.84379473 0.1141952  0.04201007]
 [0.00657326 0.97555875 0.01786798]]
my_loss:
 [0.16984483 0.82473288]
my_loss_mean:
 0.49728885581916177
tf_loss:
 [0.16984602 0.82474489]
tf_loss_mean:
 0.4972954548475541