【机器学习笔记】《统计学习方法》第二章 感知机+随机梯度下降法

主要参考书目《统计学习方法》第2版，清华大学出版社
参考书目 Machine Learning in Action, Peter Harrington
用于考研复试笔记，所以写的很简洁，自己能看懂就行。有学习需求请绕道，参考吴恩达机器学习或以上书籍，讲得比大多数博客好。

概念

感知机(perceptron)是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1，-1二值。

$f(x)=sign(w\cdot x+b)$
其中，$sign(x)=\{\begin{array}{rlr}+1,& & x\ge 0\\ -1,& & x<0\end{array}$

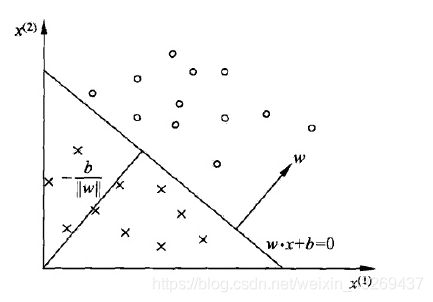
对于一个特征空间$R^n$中的一个超平面$S$,其中$w$是超平面的法向量，$b$是超平面的截距
，$S$称为分离超平面(separating hyperplane)

线性可分数据集（linearly separable data set)
被划分在超平面的两侧。

原理

感知机的学习策略

首先写出输入空间$R^n$中任一点$x_0$到超平面$S$的距离
$\frac{1}{||w||}|w\cdot x_0+b|$

书上扯淡说了个二范数，就是距离公式而已，拓展到n维空间

不考虑$||w||$感知机学习的损失函数
$L(x,b)=-\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$
其中$M$为误分类点的集合

为什么这里有一个-号？，因为认为$w\ast x_i+b>0，y_i=-1$其>0时，为+1，
比如这个图，认为超平面(分类的这根线)上面为+1，下面为-1 。 所以损失函数大于0的时候是分类正确的时候，小于或等于0则分类错误。

找到使损失函数最小的参数$w、b$就是感知机模型。

随机梯度下降法(stochastic gradient descent)

输入：训练集数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} T={ (x1​,y1​),(x2​,y2​),...,(xN​,yN​)}，其中 x i ∈ χ = R n , y i ∈ Y = { − 1 , + 1 } , i = 1 , 2 , . . . , N x_i \in \chi=R^n,y_i \in Y=\{-1,+1\}, i = 1,2,...,N xi​∈χ=Rn,yi​∈Y={ −1,+1},i=1,2,...,N学习率(learning rate)为$\eta (0<\eta \le 1)$
输入：$w、b$ 感知机模型为$f(x)=sign(w\cdot x+b)$
(1)选取初值为$w_0,b_0$
(2)在训练集中选取数据$(x_i,y_i)$
(3)如果$y_i(w\cdot x_i+b)\le 0$， // 小于等于0的时候说明分类错误，上面有提到
$w\leftarrow w+\eta y_i{x}_i$
$b\leftarrow b+\eta y_i$
turn to (2) until 训练集中没有误分类点

此处《统计学习方法》是每一轮选择一个点进行随机梯度下降，但是记得在Andrew Ng的课上说是，没更新一次都要跑一边数据集，我当时的理解是用所有数据来更新一次权值。此处应该如何，还有待考察。

如何理解？
$w\leftarrow w+\eta y_i{x}_i$
$b\leftarrow b+\eta y_i$
$y_i{x}_i$ $y_i$分别是损失函数对$w、b$的偏导，沿着梯度方向迭代。
就比如$b$，如果$y_i>0(y_i=1)$认为是错的，说明这个点在超平面上方，$b$更新后会变大，联想$y=ax+b$，那超平面就会稍微往上移动，试图把$(x_i,y_i)$包括进去。

定理2.1(Novikoff)

设数据集$T=(x_1,y_1),(x_2,y_2),...,(x_N,y_N)$是线性可分的，其中 x i ∈ χ = R n , y i ∈ { − 1 , + 1 } , i = 1 , 2 , . . . , N x_i \in \chi = R^n, y_i \in \{-1,+1\},i=1,2,...,N xi​∈χ=Rn,yi​∈{ −1,+1},i=1,2,...,N，则
(1)存在满足条件$||{\hat{w}}_{opt}||=1$的超平面${\hat{w}}_{opt}\cdot \hat{x}=w_{opt}\cdot x+b_{opt}=0$将训练集完全分开；且存在$\gamma >0$，对所有$i=1,2,...,N$
$y_i({\hat{w}}_{opt}\cdot {\hat{x}}_i)=y_i(w_{opt}\cdot x_i+b_{opt})\ge \gamma$
(2)令$R=\underset{1\le i\le N}{\max }||\widehat{x_i}||$，则感知机算法2.1在训练数据集上的误分类次数k满足不等式$k\le (\frac{R}{\gamma }{)}^2$

扯了一堆，无非就是想说
(1)如果数据集是可分这一事实的前提下，那么他一定可分，如果可分，那么一定能找到这样的超平面
(2)误分类次数是有上界的，随机梯度下降一定收敛。

关于感知机的对偶形式，请绕道
https://www.zhihu.com/question/26526858/answer/131591887

课后习题

21.为什么感知机不能表示亦或。

代码

用C++写的，以后再也不用C++写机器学习的算法了。。
算个向量都得手算。。。

偷懒维度直接写的2，认真看应该不难看懂

#include <iostream>
using namespace std;
const double eta = 1;
const double eps = 1e-5;
struct point {
    
    
    double x[3];
    int y; 
};

int cnt = 1;
void pcpt_train(point* p, double* w, double &b, int n) {
    
    
    for (int i = 1; i <= n; i++) {
    
    
        double sum = 0;
        for (int j = 1; j <= 2; j++)
            sum += w[j] * p[i].x[j];
        sum += b;
        
        if (p[i].y * sum < eps) {
    
    
            for (int j = 1; j <= 2; j++)
                w[j] += p[i].y * p[i].x[j] * eta;
            b += p[i].y * eta;
            cout << cnt++ << "\t\tx" << i << "\t\t(" << w[1] << " " << w[2] << ")\t" << b << "\t" << w[1] << "x(1)+" << w[2] << "x(2)+" << b << endl;
            pcpt_train(p, w, b, n);
            return;
        }
    }
}

int main() {
    
    
    point p[10];
    p[1].y = p[2].y = 1, p[3].y = -1;
    p[1].x[1] = p[1].x[2] = 3;
    p[2].x[1] = 4, p[2].x[2] = 3;
    p[3].x[1] = 1, p[3].x[2] = 1;

    double w[10] = {
    
     0 }; double b = 0;
    int n = 3;

    cout << "迭代次数\t误分类点数\tw\tb\tw*x+b" << endl;
    pcpt_train(p, w, b, n);

    cout << w[1] << " " << w[2] << " " << b << endl;

    return 0;
}