Part 1 什么是递归:
我们知道循环(iteration)和递归(recursion)可以理解为孪生兄弟,递归是函数抽象表达的一种。递归的优点显而易见,它在某些条件下,比循环代码量更少。递归简单来说,就是在运行过程中调用自己。而递归的实现需要满足两个条件,存在限制条件,在函数体同时在递归过程中不断逼近限制条件。(此阶段暂不考虑栈溢出)
Part 2 一些递归的问题(任何理论逃不开实例):
(1)汉诺塔问题:
首先我们要知道什么是汉诺塔问题:
这源于一个印度的传说,作者为避免文字误会,直接引用:“大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。”
简言之,现在有3个柱子,其中A柱有n个铁片从上至下为从小至大的顺序,B,C柱为空柱,需要利用B柱,将A柱上贴片转移到C柱,但是在过程中满足,大铁片不能出现在小铁片之上。
首先我们将n设置为3,观察移动过程:
借用知乎博主酱紫君gif
假设n=3的过程我们已经知道,此时我们来思考n=4时的过程
首先,我们将A上的前3个贴片移到B柱子上,则会出现下面的情景(过程一):

再将A上的最后一个贴片移到C柱上(过程2)
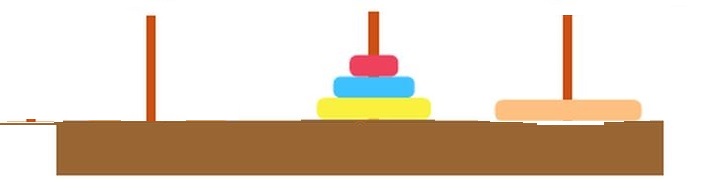
此时我们只需要将B柱子上的的三个贴片重复n=3的过程转移到C柱上(过程3)我们便完成了大业,以下是全部的过程的gif:

此时我们已经很轻松的理解了移动次数的递推公式A4=(A3)*2+1
下面我们来思考一下全过程的实现函数,首先我们来定义一下函数。
void hanoi(char A,char B,char C,int n)
这时候n=3的过程可以表示为hanoi(A,B,C,3),首先我们需要理解此函数,代表将A柱子上的n个贴片,通过B柱,移动到C柱;
在编写代码之前我们需要将n=3推广到n,我们抽象一下过程1,2,3;请记住n-1个贴片移动过程我们假设实现了!!!(此处为区别形参,实参,形参用大写表示,实参用小写)
中止条件:当n=1的时候,将1个贴片从a柱移动到c柱;
过程一:将n-1个铁片从a柱通过c柱子移动b柱;
过程二:将1个贴片从a柱移动到c柱;
过程三:将n-1个贴片从b柱通过a柱移动到c柱;
好的有了以上的过程我们的代码就写好了:
#include<stdio.h>
void hanoi(char A,char B,char C,int n)
{
if(n==1){
printf("\n move %d from %c to %c ",1,A,C);//中止条件
}else{
hanoi(A, C, B, n - 1);//将n-1个铁片从a柱通过c柱子移动b柱
printf("\n move %d from %c to %c", 1, A, C);//将1个贴片从a柱移动到c柱
hanoi(B, A, C, n - 1);//将n-1个贴片从b柱通过a柱移动到c柱
}
}
int main(){
hanoi('a', 'b', 'c', 4);
return 0;
}
运行结果是:(当然你可以将n设置为64,看看地球毁灭还有多久)
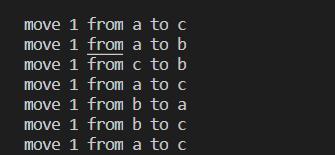
(2)青蛙跳台阶问题
问题:
青蛙一次可以跳跃两级或一级台阶,现有n级台阶,那么他有多少种跳法?
有了汉诺塔问题的思路,我们可以模仿以上思路。
中止条件:
1、当n=1时候,显然只有一种跳法;
2、当n=2时候,有两种跳法(一步两级,两次一级);
抽象过程:
先建立两个变量,最后一步跳两级的two_step,最后一步跳一级的one_step,再假设helper(n-2),helper(n-1)已经完成了,那这个问题就迎刃而解啦!代码如下:
#include <stdio.h>
int helper(int step){
if(step==1){
return 1;//中止条件
}else if(step==2){
return 2;//中止条件
}else{
int two_step = helper(step - 2);//最后一步两级
int one_step = helper(step - 1);//最后一步一级
return one_step + two_step;//所有的可能就是最后一步两级+最后一步一级嘛
}
}
int main(){
printf("%d", helper(5));
return 0;
}
(3)分巧克力问题
问题:
现有n块巧克力(函数中形参chocolate就是n),将n块巧克力分配,一份最多有limit块巧克力,那么有多少种分法呢?(假设有6块,limit为4,那么6=4+2就是一种分法)
中止条件:
1、巧克力是0块,1种分法
2、巧克力小于0块(防止多分),0种分法
3、limit是0,那么也是0种分法
抽象过程:
我们知道limit以下直至1的所有自然数都可以使用,那么我们将这一次分配分为两种情况,with_it(有这个数字,那自然总数为chocolate-limit,假设limit可重复,那么limit不改变),without_it(没有这个数字,总数还是chocolate,而limit-1了),那么代码如下:
#include<stdio.h>
int helper(int chocolate,int limit){
if(chocolate==0){
return 1;
}else if(chocolate <0){
return 0;
}else if(limit==0){
return 0;
}else{
int with_it = helper(chocolate - limit, limit);
int without_it = helper(chocolate, limit - 1);
return with_it+without_it;
}
}
int main(){
printf("%d", helper(6, 4));
return 0;
}
Part 3 递归思路的总结和迭代比较:
通过以上3个问题不难发现,递归对n的问题,我们只需要假设n-1的做法已经完成,并寻求n和n-1(甚至是n-2)之间的关系(利用n-1情况已完成去实现n),就可以弄清楚递归的总过程。另一点便是寻找中止条件,换句话说就是特殊情况,n=0,1,2时的情况。
相比于迭代,代码量明显减少。但是由于递归分为,递归前进段和递归返回段,对栈的调用极大,容易造成栈溢出。
Part 4 尾递归思考:
上文提到栈溢出的问题,我们需要一些方法去解决他,这时候尾递归便来啦!
在说明尾递归之前,我们先要知道,递归的实现过程,我们用比较简单的阶乘来描述一下:
int fact_recursion(int n){
if(n==1){
return 1;
}
return n * fact_recursion(n - 1);
}
而它的实现过程是这样的

不难发现由于递归过程,3,2,在过程中都需要占用栈来记住,当n较小时,问题不大,当n很大时,自然就栈溢出了,那我们来试一下n=100000;

那如何解决呢,我们来修改一下代码。问题的根源在于,调用过程中3,2占用了内存,那假设我们设计另一个函数,在函数每一次运行的过程中将3,2作为参数传入,是不是就可以避免了呢?
long tail_recusion_fact(long n,long result){
if(n==1){
return result;
}
return tail_recusion_fact(n - 1, result * n);
}
由于利用result这个参数去记录了每一层的结果,那就不需要栈去存储每一个3,2了
下面引用一下百科的尾递归原理:
当编译器检测到一个函数调用是尾递归的时候,它就覆盖当前的活动记录而不是在栈中去创建一个新的。编译器可以做到这点,因为递归调用是当前活跃期内最后一条待执行的语句,于是当这个调用返回时栈帧中并没有其他事情可做,因此也就没有保存栈帧的必要了。通过覆盖当前的栈帧而不是在其之上重新添加一个,这样所使用的栈空间就大大缩减了,这使得实际的运行效率会变得更高。
当然不是所有语言都支持尾递归优化。
Part 5总结:
递归是一种高效的编程技巧,在函数编写和数据结构中发挥着重要的作用。当然递归也不是万能的,毕竟电脑的算力也是有限的,有时候多写几行代码,或许比栈溢出来的更为实效哦!
