染色 概率

染色

题目描述

有个R行C列的二维表格，行的编号从上往下是0至R-1,

列编号从左往右是0至C-1，二维表格共被分成R*C个单元格子。

每个单元格子一开始都是白色。

现在要执行K条指令，每条指令的步骤是：

（1） 随机从二维表格里选取一个单元格子（不妨称为A格子）

（2） 随机从二维表格里选取一个单元格子（不妨称为B格子）

（3） 格子A和B确定了一个矩形，矩形里面所有的单元格子都会被染色。

每个单元格随机选择，均匀分布，每个选择独立于其他选择。

A和B可能对应于同一个单元格。

你的任务是：执行K条指令后，有多少个单元格子会被染上颜色？输出该期望值。

输入格式

多组测试数据

第一行，一个整数G，表示有G组测试数据。1 <= G <= 6。

每组测试数据格式：

一行，3个整数：K，R，C。0 <= K <= 100。 1 <= R,C <= 1000。

输出格式

一个实数。你的输出与标准答案的误差不能超过0.000001。

输入样例

4
1  2  1
2  2  1
1  2  2
3  5  7

输出样例

1.5
1.875
2.25
19.11917924647044

---

解题思路

题目大意：执行K条指令后，求被染上颜色的单元格子的期望值。

读过题目后，根据以前的经验，我们可以立刻发现一些思路，比如：抽到A，B两个点的概率是$(\frac{1}{R\times C}{)}^2$，这两个点组成的矩形大小是$(|x_A-x_B|+1)\times (|y_A-y_B|+1)$。

根据以上思路，我们似乎可以得到一个暴力枚举的做法，但是再仔细想想就可以发现，这根本行不通。

此时，我们不考虑矩阵内的格子被染色的期望值，我们单独考虑每一个格子被染上颜色的概率，再将它们相加求得答案。

怎么考虑每一个格子被染色的概率呢？

---

我们仔细想想，一个格子被染上1次颜色的概率是多少。

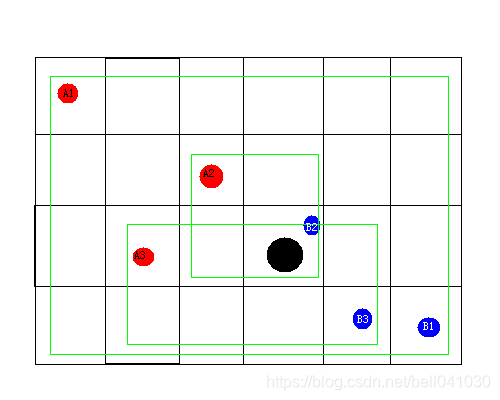
设现在考虑一个格子$P(x,y)$，要让它染上颜色，我们可以怎样选取A，B？

可以这么取：

这种做法的弊端是：

• 可取的两个点很多很多
• 执行多条指令会重复计算

---

我们需要找到一个简便的方法去解决这个问题，不知大家看过我写的进球数没有：

将以上三种情况的概率求出来相加，就是答案了。但是，除此之外还有一种更简单的方法。

至少有一支球队的进球数为质数的概率=1-两支球队进球数都是非质数的概率

我们在本题也可以沿用答案=1-非答案的办法，这就使得问题简单多了。

---

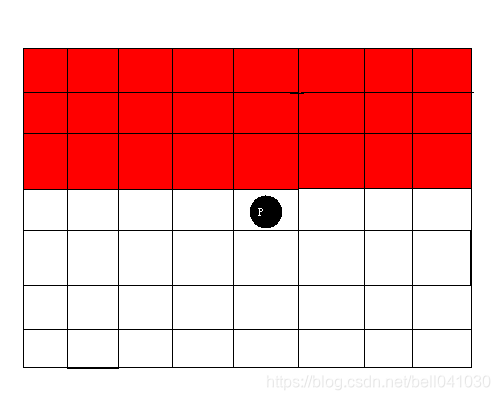
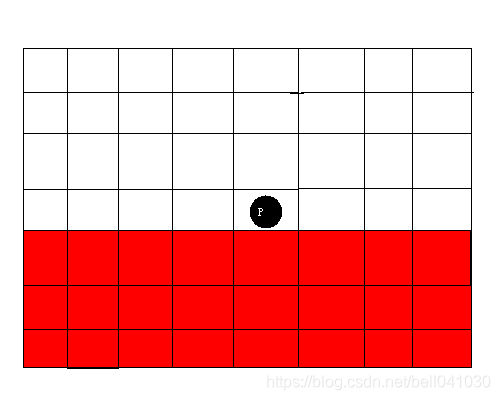
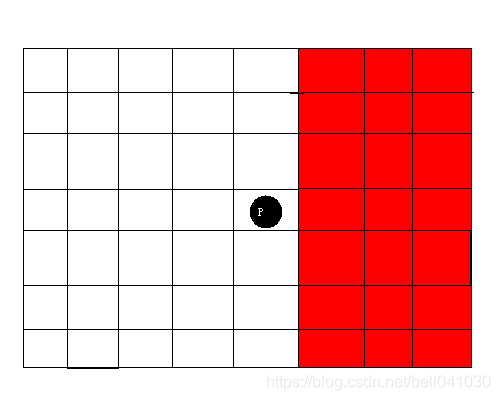
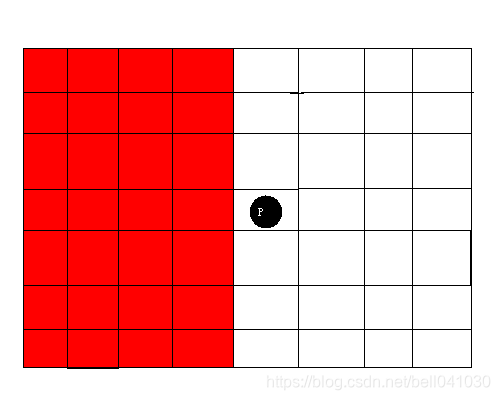
单独考虑一个格子$P(x,y)$在执行$K$条指令后都不能被染上颜色的概率。

那么，格子不能被染上颜色的概率的情况是两次选点都选在红色区域：




我们只要计算A，B在执行K条指令后都落在红色区域内的概率在去掉重复计算的部分就可以求得最终的答案了。

---

代码

#include<iostream>
#include<fstream>
#include<cstdio>

using namespace std;
int G,K,R,C;
double s1,s2,s3,s4,s5,s6,s7,s8,prob,temp,temp2;

int main()
{
    
    
	freopen("2805.in","r",stdin);
	freopen("2805.out","w",stdout);
	cin>>G;
	for(int gr=1;gr<=G;gr++)
	{
    
    
		cin>>K>>R>>C;
		prob=0.0;
		for(int i=1;i<=R;i++)
		{
    
    
			for(int j=1;j<=C;j++)
			{
    
    
				s1=(i-1)*C;//above
				s2=(R-i)*C;//under
				s3=R*(j-1);//left
				s4=R*(C-j);//right
				s5=(i-1)*(j-1);//up&left
				s6=(i-1)*(C-j);//up&right
				s7=(R-i)*(j-1);//down&left
				s8=(R-i)*(C-j);//down&right
				/********************两次选点都无法将P(i,j)染上颜色的概率***********************/
				temp2=0.0;
				temp2+=(s1/double(R*C)*s1/double(R*C));
				temp2+=(s2/double(R*C)*s2/double(R*C));
				temp2+=(s3/double(R*C)*s3/double(R*C));
				temp2+=(s4/double(R*C)*s4/double(R*C));
				temp2-=(s5/double(R*C)*s5/double(R*C));
				temp2-=(s6/double(R*C)*s6/double(R*C));
				temp2-=(s7/double(R*C)*s7/double(R*C));
				temp2-=(s8/double(R*C)*s8/double(R*C));
				/********************************************************************************/
				temp=1.00;
				for(int l=1;l<=K;l++)
					temp*=temp2;
				prob+=1.00-temp;
			}
		}
		printf("%.6lf\n",prob);
	}
	return 0;
}