博客内容主要是以 北京大学 屈婉玲老师的 MOOC 视频来写的。视频共是十周的内容,我决定用五篇博客完成。
温馨提示:这个课程不仅适用于 算法设计与分析 的学习,也非常适用于 数学建模 的学习,如果是学习 数学建模的基础部分,前两周的内容是非常适合的,如果要进一步学习 建模思想,建议把这十周视频好好看一遍。( •̀ ω •́ )y
我们还是先来看一下这十周视频的思维导图:
在这篇博客中写的是九、十周的内容:回溯与分支限界。
第九周
回溯算法的例子
4 后问题:
搜索空间:4叉树。
0-1 背包问题:
搜索空间:子集树,有 2^n 片树叶。
货郎问题:
搜索空间:排列数,有 (n-1)! 片树叶。
上面三个例子的共同点:解都是向量。
搜索空间在上面已经说明,树的结点对应于部分向量,可行解是叶结点。
搜索方法:深度优先,宽度优先,跳越式遍历搜索树等。
回溯算法的设计思想和适用条件
深度与宽度优先搜索的例子:
回溯算法基本思想:
(1)适用:求解搜索问题和优化问题。
(2)搜索空间:树,结点对应部分解向量,可行解在树叶上。
(3)搜索过程:采用系统的方法隐含遍历搜索树。
(4)搜索策略:深度优先,宽度优先,函数优先,宽深结合等。
(5)结点分支判定条件:满足约束条件——分支扩张解向量,不满足约束条件,回溯到该结点的父结点。
(6)结点状态:动态生成
(7)存储:当前路径
回溯算法的适用条件:多米诺性质
回溯算法的设计步骤:
回溯算法实现及实例
回溯算法的实现:递归实现、迭代实现
实例:装载问题
最坏情况下时间复杂度 O(2^n)。
图的着色
着色问题的描述
着色问题的算法设计
时间复杂度及改进途径
着色问题的应用
搜索树结点数的估计
Monte Carlo 方法
目的:估计搜索树真正访问结点数
步骤:
随机抽样,选择一条路径,用这条路径代替其他路径,
逐层累加树的结点数,多次选择,取结点数的平均值。









第十周
分支限界
分支限界适用于组合优化问题。
对结点<x1,x2,…,xk>定义代价函数,对当前结点为根子树的可行解的上界或下界(极大化问题与极小化问题的区别)
定义界的初值
得到新的更好的可行解就更新界。
组合优化问题的相关概念:
目标函数(极大化或极小化)
约束条件(解满足的条件)
可行解:搜索空间满足约束条件的解
最优解:使得目标函数达到极大(或极小)的可行解
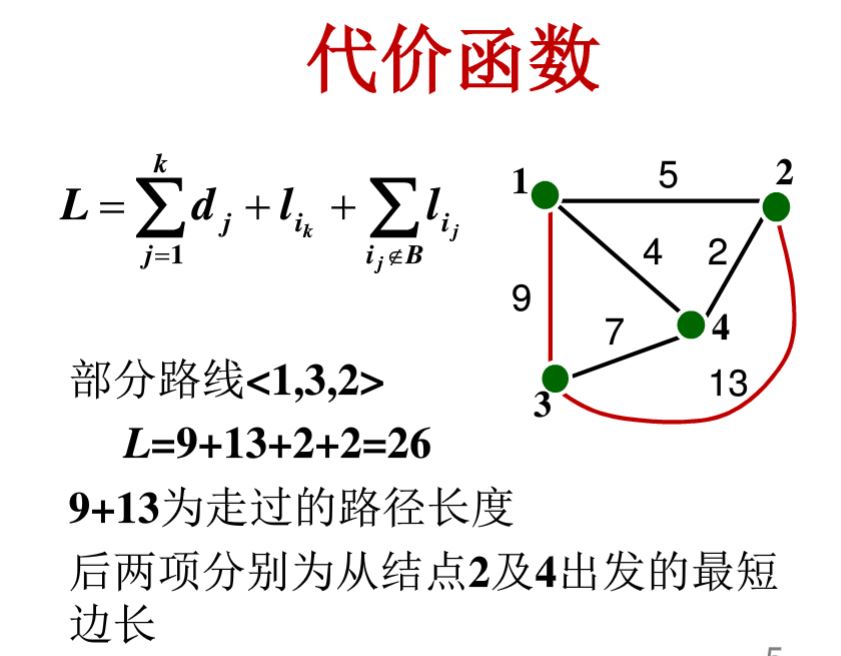
代价函数:
计算位置:搜索树的结点
值:极大化问题是以该点为根的子树所有可行解的值的上界(极小化问题为下界)
性质:对极大化问题父结点代价不小于子结点的代价(极小化问题相反)
界:
含义:当前得到可行解的目标函数的最大值(极小化问题相反)
初值:极大化问题的初值为0(极小化问题为最大值)
更新:得到更好的可行解时
分支限界:
停止分支回溯父结点的依据:
(1)不满足约束条件
(2)对于极大化问题,代价函数值小于当前界(对于极小化问题是大于界)
界的更新:
对极大化问题,如果一个新的可行解的优化函数值大于(极小化问题为小于)当前的界,则界更新为该可行解的值。
最大团问题
最大团问题的定义;
最大团与点独立集的关系;
分支限界算法的设计
树的结构:子集树
分支约束条件
代价函数与界的设定
最坏情况的时间复杂度:O(n2^n)
货郎问题
货郎问题的分支限界算法:
约束条件:只能选没有走过的结点
代价函数:走过的长度+后续长度的下界
时间复杂度:O(n!)
圆排列问题
圆排列问题的定义
如何设计代价函数:已有的排列长度+后续的圆排列长度的下界
时间复杂度估计:O((n+1)!)
连续邮资问题




九、十周小结
1.回溯法适用于求解组合搜索问题及优化问题。
2.求解条件:满足多米诺性质。
3.解的表示:解向量,求解是不断扩充解向量的过程。
4.回溯条件:
搜索问题——约束条件
优化问题——约束条件+代价函数
5.分支策略:深度优先、宽度优先、宽深结合、函数优先。
6.结点状态
7.算法时间复杂度:W(n) = ( p(n)f(n) )
其中,p(n) 为每个结点的工作量,f(n) 为结点个数。
最坏情况下时间通常为指数级,平均情况下比蛮力算法好,空间代价小。、
8.降低时间复杂性的主要途径:
(1)根据树的分支设计优先策略,结点少分支优先,解多分支优先;
(2)利用搜索树的对称性裁剪子树;
(3)分解为子问题,若求解时间 f(n) = c2^n,
组合时间为 O( 2^(n/k) ) ,分解为 k 个 n/k 规模子问题,则该算法时间为
T(n) = kc2^(n/k) + O( 2^(n/k) ) = O( 2^(n/k) ) = o(2^n)
课程总结
基础知识
函数的阶、序列求和、递推方程求解、算法设计技术
分治策略
适用条件:归约为独立求解子问题。
设计步骤:归约方法,初始子问题的计算,子问题解的综合方法。
注意子问题划分均衡,类型相同。
递归算法分析:求解递推方程。
改进途径:减少子问题数,预处理。
典型问题:二分检索,归并排序,芯片测试,幂乘,矩阵乘法,最临近点对,多项式求值。
动态规划
适用条件:优化问题,多步判断求解,满足优化原则,子问题重叠。
设计步骤:确定子问题边界,列关于目标函数的递推方程及初值;自底向上,备忘录存储;标记函数及解的追踪方法。
复杂度分析:备忘录,递推方程。
典型问题:矩阵链相乘、投资、背包、最长公共子序列、图像压缩、最大子段和、最优二分检索树、生物信息学应用。
贪心法
适用条件:组合优化问题,多步判断求解,有贪心选择性质。
设计步骤:局部优化策略的确定及算法正确性证明(直接证明、数学归纳法、交换论证)
复杂度分析
典型问题:活动选择、装载问题、最小延迟调度、最优前缀码、最小生成树、单源最短路。
回溯和分支限界
适用条件:搜索或优化问题,多步判断求解、满足多米诺性质。
设计步骤:确定解向量、搜索树结构、搜索顺序、结点分支搜索的约束条件与代价函数、路径存储。
搜索树结点数估计
复杂度分析
典型问题:n后问题、背包问题、货郎问题、装载问题、最大团问题,圆排列问题,连续邮资问题。
算法设计
设计思想:尽量选复杂度低的算法
算法实现依赖于数据结构,选择合适的数据结构
实际问题中的综合考虑:时空权衡、实现成本的权衡…