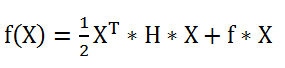01线性规划
Matlab求解线性规划命令:[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
这里 fval 返回目标函数的值,LB 和 UB 分别是变量 x 的下界和上界,x0是x的初始值,OPTIONS 是控制参数。
例题(e01)求解以下线性规划问题

matlab求解线性规划问题,要统一将大于等于化为小于等于
c=[2;3;-5];
a=[-2 5 -1;1 3 1];
b=[-10;12];
aeq=[1 1 1];
beq=7;
x=linprog(-c,a,b,aeq,beq,zeros(3,1));
value=c'*x;
fprintf('x1=%.4f,x2=%.4f,x3=%.4f\nz:%.4f\n',x,value);
结果:
x1=6.4286,x2=0.5714,x3=0.0000
z:14.571402整数规划
求解方法
1.分支定界法—可求解纯整数或混合整数线性规划
2.割平面法—可求解纯整数或者混合整数线性规划
3.隐枚举法—求解“0-1”整数规划
4.蒙特卡洛法—可求解各种类型规划问题
02.1分支定界法
对有约束条件的最优化问题(其可行解为有限数)的所有可行解空间恰当地进行系统搜索,这就是分枝与定界内容。通常,把全部可行解空间反复地分割为越来越小的子集,称为分枝;并且对每个子集内的解集计算一个目标下界(对于最小值问题),这称为定界。在每次分枝后,凡是界限超出已知可行解集目标值的那些子集不再进一步分枝,这样,许多子集可不予考虑,这称剪枝。这就是分枝定界法的主要思路。
例子(e02)求解以下整数规划问题

1. 先不考虑整数限制,即解相应的线性规划,得最优解为:
x1=4.8092,x2=1.8168,z=355.8779
上述解不符合整数条件。这时z是问题的最优目标函数值的上界。而x1=0,x2=0取到下界,因而实际解的范围为:0<=z<=356
2.分支。 取x1<=[4.8092]=4;x1>=[408092]+1=5
则问题进一步分解为:

此时B1的解为:x1=4,x2=2.1,z1=349;B2的解为:x1=5;x2=1.57,z2=341.4。
由此可知最优解范围为0<=z<=349
分支定界法求解:
3.对B1再次分界求解得到
B11:x1=4,x2=2,z11=340
B12:x1=1.43,x2=3,z12=327.14
4.对B2进行分支求解得到
B21:x1=5.44,x2=1,z21=308
B22无可行解
将B21和B22剪枝,得到原问题的最优解:
x1=4,x2=2,z=340
02.2隐枚举法
因为穷举法的解空间太大,往往无法实现穷举,因此常设计一些方法,只检查变量取值的组合的一部分,就能求到问题的最优解。这样的方法称为隐枚举法。
例子(e04):求解以下0-1规划问题

方法:
1.先试探性求一个可行解,易看出(x1,x2,x3)=(1,0,0)满足约束条件,故为一个可行解,且 z=3
2.因为是求极大值问题,故求最优解时,凡是目标值 3 < z 的解不必检验是否满足约束条件即可删除,因它肯定不是最优解,于是应增加一个约束条件(目标值下界)
3.改进过滤条件
4.由于对每个组合首先计算目标值以验证过滤条件,故应优先计算目标值 z 大的组合,这样可提前抬高过滤门槛,以减少计算量
02.3蒙特卡洛法
由于使用枚举法的解空间太大,因此可以使用概率的方法随机选择部分解进行验证,这样当随机解足够多时便能大概率获得最优解,这便是蒙特卡洛法的思想。
例子(e05):求解以下非线性规划的问题

分析:如果用枚举法计算,那么解空间数目为1005100^5,计算量巨大,如果使用蒙特卡洛法随机计算10610^6 个点,则可以使用概率论方法证明取到最优值的概率为:0.999954602。编写matlab程序求解
function [f,g]=mengte(x)
f=x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)-8*x(1)-2*x(2)-3*x(3)-...
x(4)-2*x(5);
g=[sum(x)-400
x(1)+2*x(2)+2*x(3)+x(4)+6*x(5)-800
2*x(1)+x(2)+6*x(3)-200
x(3)+x(4)+5*x(5)-200];rng(sum(clock));
p0=0;
tic
for i=1:10^6
x=99*rand(5,1);
x1=floor(x);x2=ceil(x);
[f,g]=mengte(x1);
if sum(g<=0)==4
if p0<=f
x0=x1;p0=f;
end
end
[f,g]=mengte(x2);
if sum(g<=0)==4
if p0<=f
x0=x2;p0=f;
end
end
end
fprintf('x1=%.0f\nx2=%.0f\nx3=%.0f\nx4=%.0f\nx5=%.0f\nz=%.0f\n',x0,p0);
toc结果:
>> e05
x1=4
x2=99
x3=14
x4=99
x5=6
z=49238
时间已过 1.861732 秒。03非线性规划
定义:如果目标函数或约束条件中包含非线性函数,就称这种规划问题为非线性规划问题。
Matlab中的非线性规划标准型:

其中f(x)是标量函数, A,B,Beq Aeq是相应维数的矩阵和向量,C(x),Ceq(x)是非线性向量函数。
Matlab中求解命令是:X=FMINCON(FUN,X0,A,B,Aeq,Beq,LB,UB,NONLCON,OPTIONS)

function f=fun1(x)
f=sum(x.^2)+8;
endfunction [g,h]=fun2(x)
g=[-x(1)^2+x(2)-x(3)^2
x(1)+x(2)^2+x(3)^3-20];
h=[-x(1)-x(2)^2+2
x(2)+2*x(3)^2-3];
end
options=optimset('largescale','off');
[x,y]=fmincon('fun1',rand(3,1),[],[],[],[],zeros(3,1),[],'fun2', options);
fprintf('x1=%.4f\nx2=%.4f\nx3=%.4f\ny=%.4f\n',x,y);结果:
>> e06
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the default value of the optimality tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.
<stopping criteria details>
x1=0.5522
x2=1.2033
x3=0.9478
y=10.651104二次规划
定义:二次规划为非线性规划的一种,若某非线性规划的目标函数为自变量x的二次函数,约束条件又全是线性的,就称这种规划为二次规划。
Matlab中的二次规划标准形表示为:

这里H是实对称矩阵,f,b是列向量,A是相应维数的矩阵。
Matlab求解:quadprog()

H,f 是把目标函数化成标准形式后得到的实对称矩阵和列向量。显然H应当是原函数的海森矩阵。 它的返回值是向量x,X0是x的初始值;A,B,Aeq,Beq定义了线性约束。
例子(e07)求解以下二次规划问题

求解前,需要将目标二次函数化为标准形式:
h=[4,-4;-4,8];
f=[-6;-3];
a=[1,1;4,1];
b=[3;9];
[x,value]=quadprog(h,f,a,b,[],[],zeros(2,1));
fprintf('x1=%.4f\nx2=%.4f\nz=%.4f\n',x,value);
x1=0:0.01:3;x2=x1;
[x1,x2]=meshgrid(x1,x2);
f=2*x1.^2-4*x1.*x2+4*x2.^2-6*x1-3*x2;
f(x1+x2<=3 & 4*x1+x2<=9)=-15;
mesh(x1,x2,f);
结果:
>> e07
Minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the default value of the optimality tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.
<stopping criteria details>
x1=1.9500
x2=1.0500
z=-11.0250