AtCoder Regular Contest 089

D Checker
k比较小，对所有位置进行 ${mod(2*k)}$ ，然后把棋盘扩展为原来的四倍，枚举起点，用二维前缀和就可以做出来了。

#include<bits/stdc++.h>
using namespace std;
const int N=4e3+5;
int n,k,a[N][N],b[N][N];
int getsuma(int x,int y)
{
    
    
    if(x<0||y<0) return 0;
    return a[x][y];
}
int getsumb(int x,int y)
{
    
    
    if(x<0||y<0) return 0;
    return b[x][y];
}
int querya(int x1,int y1,int x2,int y2)
{
    
    
    return getsuma(x2,y2)-getsuma(x2,y1-1)-getsuma(x1-1,y2)+getsuma(x1-1,y1-1);
}
int queryb(int x1,int y1,int x2,int y2)
{
    
    
    return getsumb(x2,y2)-getsumb(x2,y1-1)-getsumb(x1-1,y2)+getsumb(x1-1,y1-1);
}
int solve(int sx,int sy,int c)
{
    
    
    int ans=0;
    if(c)
    {
    
    
        ans+=querya(sx+0,sy+0,sx+k-1,sy+k-1);
        ans+=querya(sx+k,sy+k,sx+2*k-1,sy+2*k-1);
        ans+=queryb(sx+0,sy+k,sx+k-1,sy+2*k-1);
        ans+=queryb(sx+k,sy+0,sx+2*k-1,sy+k-1);
    }
    else
    {
    
    
        ans+=queryb(sx+0,sy+0,sx+k-1,sy+k-1);
        ans+=queryb(sx+k,sy+k,sx+2*k-1,sy+2*k-1);
        ans+=querya(sx+0,sy+k,sx+k-1,sy+2*k-1);
        ans+=querya(sx+k,sy+0,sx+2*k-1,sy+k-1);
    }
    return ans;
}
int main()
{
    
    
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)
    {
    
    
        int x,y;char z;scanf("%d %d %c",&x,&y,&z);
        x%=(2*k);y%=(2*k);
        if(z=='B') a[x][y]++;
        else b[x][y]++;
    }
    for(int i=0;i<2*k;i++)
        for(int j=0;j<2*k;j++)
    {
    
    
        a[i+2*k][j+2*k]=a[i+2*k][j]=a[i][j+2*k]=a[i][j];
        b[i+2*k][j+2*k]=b[i+2*k][j]=b[i][j+2*k]=b[i][j];
    }
    for(int i=0;i<4*k;i++)
        for(int j=1;j<4*k;j++)
        a[i][j]+=a[i][j-1],b[i][j]+=b[i][j-1];
    for(int i=1;i<4*k;i++)
        for(int j=0;j<4*k;j++)
        a[i][j]+=a[i-1][j],b[i][j]+=b[i-1][j];
    int ans=0;
    for(int i=0;i<k;i++)
        for(int j=0;j<k;j++)
    {
    
    
        ans=max(ans,solve(i,j,0));
        ans=max(ans,solve(i,j,1));
    }
    printf("%d\n",ans);
}

E GraphXY
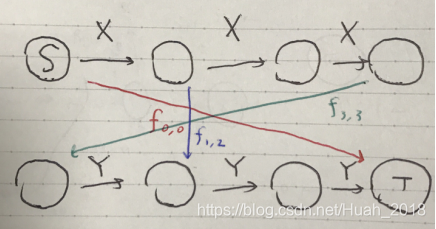
在这里插入图片描述
我们构造这样一张图，那么一条路径就是，把上面第i个点连到下面倒数第j个点的边称为 ${f_{i,j}}$ ，那么经过边 ${f_{i,j}}$ 的距离就是 ${f_{i,j}+i*x+j*y}$ 。

对于 ${1<=x<=a,1<=y<=b}$ ，有 ${d_{x,y}=min(f_{i,j}+i*x+j*y)}$ ，那么每一对 ${(x,y)}$ 都给了 ${f_{i,j}}$ 一个约束 ${f_{i,j}=d_{x,y}-i*x-j*y}$ 。注意到对于两对不同的 ${(x,y)}$ ，如 ${(x_1,y_1),(x_2,y_2)}$ ，设 ${f_{i,j,1}=d_{x_1,y_1}-i*x_1-j*y_1,f_{i,j,2}=d_{x_2,y_2}-i*x_2-j*y_2}$ ，如果 ${f_{i,j,1}<f_{i,j,2}}$ ,我们只能使得 ${f_{i,j}=f_{i,j,2}}$ ，否则有 ${f_{i,j,1}+i*x_2+j*y_2<d_{x_2,y_2}}$ ，即当 ${x=x_2,y=y_2}$ 时我们有更小的路径可以走，这不符合题意。

因此我们使得 ${f_{i,j}=max(d_{x,y}-i*x-j*y)}$ ，枚举 ${x,y,i,j}$ 时间复杂度为 ${O(n^3)}$ 。

算出 ${f_{i,j}}$ 后再验证一下即可。

#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
const int N=105;
int a,b,f[N][N],d[N][N],s[N][N];
int main()
{
    
    
    scanf("%d%d",&a,&b);
    for(int x=1;x<=a;x++)
        for(int y=1;y<=b;y++)
        scanf("%d",&d[x][y]);
    for(int i=1;i<=101;i++)
        for(int j=1;j<=101;j++)
        for(int x=1;x<=a;x++)
        for(int y=1;y<=b;y++)
        f[i][j]=max(f[i][j],d[x][y]-(i-1)*x-(101-j)*y);
    memset(s,inf,sizeof(s));
    for(int i=1;i<=101;i++)
        for(int j=1;j<=101;j++)
            for(int x=1;x<=a;x++)
            for(int y=1;y<=b;y++)
            s[x][y]=min(s[x][y],f[i][j]+(i-1)*x+(101-j)*y);
    for(int x=1;x<=a;x++)
        for(int y=1;y<=b;y++)
        if(d[x][y]!=s[x][y])
    {
    
    
        printf("Impossible\n");
        return 0;
    }
    printf("Possible\n");
    printf("202 %d\n",100+100+101*101);
    for(int i=1;i<101;i++)
        printf("%d %d X\n",i,i+1);
    for(int i=1;i<101;i++)
        printf("%d %d Y\n",101+i,101+i+1);
    for(int i=1;i<=101;i++)
        for(int j=1;j<=101;j++)
        printf("%d %d %d\n",i,j+101,f[i][j]);
    printf("%d %d\n",1,202);
}

F ColoringBalls
对于一个合法的颜色序列，我们把白色的球全部删掉，那么序列被划分成了若干段，在每一段中，我们把相邻的颜色相同的小球合并，那么每一段序列变成了一段红蓝交替的序列。
如：
”WRRBRBBWWRRRRWRBBWWRRBBRR”->
{“RRBRBB”, “RRRR”, “RBB”, “RRBBRR”}->
{“RBRB”, “R”, “RB”, “RBR”}

我们考虑每个连续段中蓝球的数量，如果没有蓝球，那么序列为“R”，我们至少需要一次‘r’操作,如果序列为‘B’，我们至少要先操作一次‘r’，然后操作一次’b’，即操作‘rb’。
如果序列为‘BRB’，即有两个蓝球，我们进行操作‘rbr’，‘rbb’，显然通过顺序不同，都可以达成。
通过推导我们可以得出如下结论：
1 r-------------------->R
2 rb------------------>B（BR,RB,RBR）
3 rb?---------------->BRB（RBRB,BRBR,RBRBR）
4 rb??-------------->BRBRB （RBRBRB,BRBRBR,RBRBRBR）
…

右边的颜色序列经过左边最少的操作次数就可以得出来，？表示任意操作。

现在让我们考虑如何计数，我们通过从小到大搜索操作序列的长度，然后将操作序列之间的关系进行排列，就可以得出答案，因为n只有70，从小到大不降的对70进行n进行整数划分搜索出来没多大。

那么对于一种操作序列如何计数？
假如操作序列时1，3，4，那么我们的序列至少要为
R_BRB_BRBRB(_表示白球)

考虑现在还剩余sum个小球没有染色，我们要将这sum个小球插入相应位置进行染色。
如果插入的小球是白球，可以把这个小球插入到两个白球的位置，或者插在两边，假设存在cnt个操作序列，那么有cnt+1个位置可选。

扫描二维码关注公众号，回复： 11697021 查看本文章

我们还可以和其它每个R或者B合成一个颜色相同连续的序列，那么方案数为当前已经固定了的球的个数，注意到当操作序列长度>=2，我们还可以额外选择在其两边染成红球，额外多出两种方案

那么假如一共s中方案，就相当于把sum个小球分成s组，使用隔板法，在sum个小球中放入s-1个小球，再选出s-1个作为隔板，序列就分成了s组。方案数为C(sum+s-1,s-1)。然后对不同操作序列排列组合一下即可求出答案。

注意到我们还有判断序列的合法性，贪心的来说长度>=2要先选择最靠左的rb，==1的接着选择靠左的r。在从右往左扫一遍判断数量是否合法即可。这个地方相信网上的题解都提到过了，实在不会可以上网去搜题解，这里就不再详细描述了。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=205,mod=1e9+7;
ll ans,f[N],invf[N];
ll C(int n,int m)
{
    
    
    return f[n]*invf[n-m]%mod*invf[m]%mod;
}
int n,k,tot,cnt,pos[N],l[N],p[N],vv[N];
char s[N];
bool vis[N];
bool check()
{
    
    
    memset(vis,false,sizeof(vis[0])*(k+3));
    memset(vv,0,sizeof(vv[0])*(k+3));
    if(cnt>tot) return false;
    int j=1;
    for(int i=cnt;i>=1;i--)
    {
    
    
        int x=pos[j++];
        vis[x]=true;
        if(l[i]>=2)
        {
    
    
            if(!p[x]) return false;
            vis[p[x]]=true;
            vv[p[x]]=i;
        }
        else vv[x]=i;
    }
    int sum=0;
    for(int i=k;i>=1;i--)
        if(!vis[i]) sum++;
        else if(vv[i])
        {
    
    
            int x=max(0,l[vv[i]]-2);
            if(sum<x) return false;
            sum-=x;
        }
    return true;
}
bool dfs(int mn,int dep,int len)
{
    
    
    cnt=dep;
    if(!check()) return false;
    int s=dep+1;
    for(int i=1;i<=dep;i++)
        if(l[i]==1) s++;
    else s+=2*(l[i]-1)-1+2;
    ll res=C(n-len+s-1,s-1)*f[dep]%mod;
    int t=1;
    for(int i=2;i<=dep;i++)
        if(l[i]!=l[i-1]) res=res*invf[t]%mod,t=1;
    else t++;
    res=res*invf[t]%mod;
    ans=(ans+res)%mod;
    if(dep+1>tot) return true;
    for(int i=mn;i<=k;i++)
    {
    
    
        int nlen=len;
        if(dep!=0) nlen++;
        if(i<=2) nlen++;
        else nlen+=2*(i-1)-1;
        if(nlen>n) break;
        l[dep+1]=i;
        if(!dfs(i,dep+1,nlen)) break;
    }
    return true;
}
int main()
{
    
    
    f[0]=invf[0]=f[1]=invf[1]=1;
    for(int i=2;i<N;i++) f[i]=f[i-1]*i%mod,invf[i]=(mod-mod/i)*invf[mod%i]%mod;
    for(int i=2;i<N;i++) invf[i]=invf[i-1]*invf[i]%mod;
    scanf("%d%d",&n,&k);
    scanf("%s",s+1);
    for(int i=1;i<=k;i++)
        if(s[i]=='r')
    {
    
    
        pos[++tot]=i;
        for(int j=i+1;j<=k;j++)
            if(!vis[j]&&s[j]=='b')
        {
    
    
            p[i]=j;vis[j]=true;break;
        }
    }
    dfs(1,0,0);
    printf("%lld\n",ans);
}

AtCoder Regular Contest 089

猜你喜欢