【数据库原理】关系数据库理论(二)

函数依赖.

关系模式中各属性之间的相互依赖、相互制约的联系称为数据依赖，数据依赖又分为函数依赖和多值依赖，其中函数依赖最为重要。

函数依赖(Function Dependency，FD)是关系模式中属性之间的一种逻辑关系依赖。

例如在关系数据库理论(一)中的SCD表中，【SNo】和【SN、Age、Dept】之间就有一种逻辑依赖关系。当一个SNo确定下来以后，对应的学生就确定了，他的姓名SN，年龄Age以及所属的系别Dept都被确定了。这就类似于数学中的函数定义y=f(x)，x可以唯一确定y的值，对于同一个x值，不会有多个y值与它对应。现在自变量是【SNo】，因变量是【SN、Age、Dept】，我们说SNo的值唯一地决定函数(SN,Age,Dept)的值。函数依赖形式化的定义如下所示：

有关函数依赖有下面几点需要说明：

• 【平凡函数依赖】在定义中，如果属性集Y是属性集X的子集，则必然存在着函数依赖X→Y，这样的函数依赖就称为平凡函数依赖。对应地，如果Y不是X的子集，就是非平凡函数依赖，前者并没有实际的意义，所以我们讨论的都是非平凡函数依赖，只有它才和完整性约束条件有关。
• 【语义范畴】需要注意的是，函数依赖是一个语义范畴的概念，它是无法通过形式化证明一个函数依赖是否成立的，它实质上是对于现实世界中的事物及其相关性的一种断言。例如在学生关系表S中，我们如果认为学生不会出现重名的情况，就能得到SN→Age以及SN→Dept这样的函数依赖，但这样的函数依赖仅仅成立于没有学生重名的情况下
• 【联系类型】函数依赖与属性之间的联系类型有关，若X和Y有着1:1的联系，那么就存在X→Y以及Y→X；若X和Y有着m:1的联系，则只存在函数依赖X→Y，例如SNo与Age就是多对一的关系，所以有SNo→Age；如果X和Y是m:n的关系，那么X和Y之间就不存在任何函数依赖关系。
• 【关于定义】定义中:
  意思是说，对于r的任意两个元组$t_1$和$t_2$，只要有$t_1[X]=t_2[X]$，就有$t_1[Y]=t_2[Y]$

逻辑蕴含.

假设已知关系模式R(X,Y,Z)，并且有函数依赖X→Y，Y→Z，问是否有X→Z？能否从已知的函数依赖中得到函数依赖XY→YZ？
类似上面这种从一组已知的函数依赖中，判断一些函数依赖是否成立或者能否从前面已知的函数依赖推导出后面的函数依赖，就是逻辑蕴含所要涉及的内容。

简言之，如果能够从F中推导出X→Y，就说F逻辑蕴含X→Y.

函数依赖的推理规则.

在逻辑蕴含部分我们意识到一些推理规则的必要性，从已知的函数依赖中，我们需要知道哪些函数依赖是能够被得出的，函数依赖的推理规则最早出现在1974年W.W.Armstrong的论文中。
所有的规则介绍中的符号说明如下：设有关系模式R(U)，U是关系模式R的属性集，F是R上成立的、只涉及U中属性的函数依赖集。X、Y、Z、W均是U的子集，r是R的一个实例。

Armstrong公理.

【①自反律Reflexivity】

证明：因为Y是X的子集，若r中的两个元组在X上的值相等，那么它们在Y上的值也必然相等。

【②增广律Augmentation】

证明：假设在条件之下，结论不成立，也就是说当$t_1[XZ]=t_2[XZ]$时，有$t_1[YZ]\ne t_2[YZ]$，也就是存在$t_1[Y]\ne t_2[Y]$或$t_1[Z]\ne t_2[Z]$。前一种情况与自反律相矛盾，后一种情况与条件$t_1[XZ]=t_2[XZ]$矛盾，所以假设不成立，即增广律是正确的。

【③传递律Transitivity】

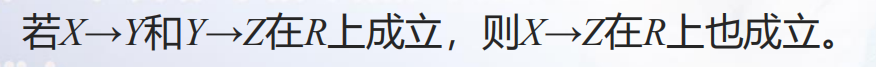
证明：假设该条件之下，结论不成立，即$t_1[X]=t_2[X]$时，有$t_1[Z]\ne t_2[Z]$.在这样的假设下，$t_1$和$t_2$在属性集Y上的情况只有两种：$t_1[Y]=/\ne t_2[Y]$，如果等于，则与Y→Z矛盾；否则就与X→Y矛盾，因此假设不成立，所以传递律是正确的。

Armstrong公理推论.

【①合并律Union】

证明：已知X→Y，用增广律两边加上X，得到XX→XY，同理X→Z得到XY→YZ，再根据传递律，得到XX→YZ，即X→YZ.

【②伪传递律Pseudotransitivity】

证明：已知X→Y，用增广律两边加上W，得到XW→YW，再根据传递律，得到XW→Z.

【③分解律Decomposition】

证明：根据自反律有Y→Z，再根据传递律得到X→Z.
有了分解律以及合并律之后，我们有如下这个定理：

【④复合律Composition】

证明：根据增广律以及X→Y得到XW→YW，同理有YW→YZ，再根据传递律就有XW→YZ.