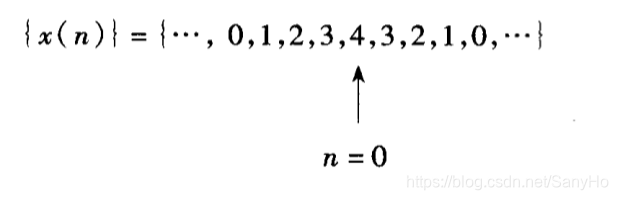2.1.4 离散信号的描述
无论是采样得到的离散信号,还是客观事物给出的离散信号,只要给出函数值的离散时刻是等间隔的,我们都可以用序列
x(n)来表示它们,这里n是各函数值在序列中出现的序号。
通常可以用
x(n)在整个定义域内的一组有序数列的集合
{x(n)}来表示一个离散信号,例如
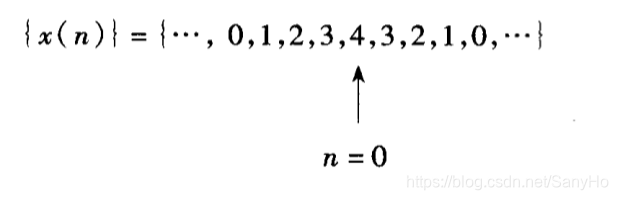
表示了一个离散信号,n值规定为自左向右逐一递增。显然,这里
x(0)=4,x(1)=3,⋯。
如果
x(n)有闭式表达式,离散信号也可以用闭式表达式表示。例如上述的离散信号可表示为
x(n)=⎩⎪⎪⎪⎨⎪⎪⎪⎧04−n4+n04≤n<∞0≤n<4−3≤n<0∞<n<−3
或者表示为
x(n)=4−∣n∣,∣n∣≤3
式中对
∣n∣>3的
x(n)值默认为零。
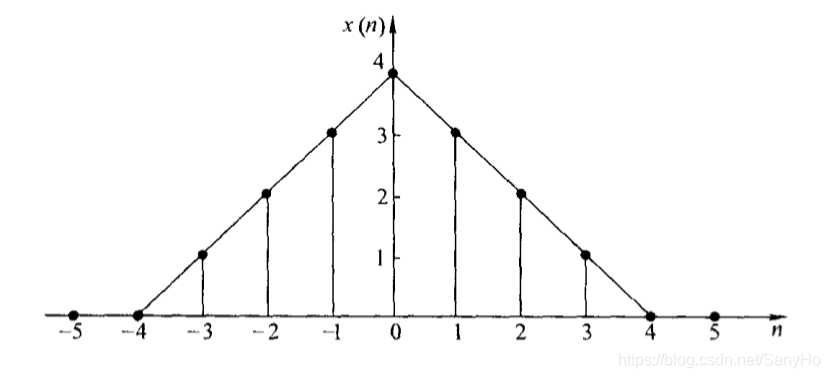
离散信号也常用图形表示,下图描述了离散信号,有时,也可以将它们的端点连接在一起,以表示信号的变化规律,
x(n)只有在n的整数值才有定义。
与连续信号类似,也可定义离散信号的能量
W=n=−∞∑∞∣x(n)∣2
下面给出集中常用的典型离散信号(典型序列):
- 单位脉冲序列
δ(n)={10n=0n=0
此序列只在n=0处取单位值1,如下图所示。
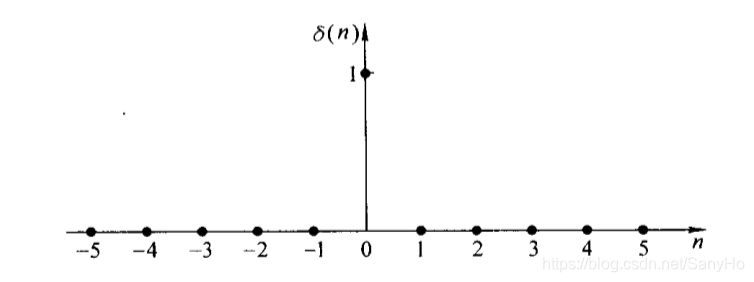
类似与连续信号中的单位冲激函数
δ(t),它也具有取样特性,如
x(n)δ(n)=x(0)δ(n)x(n)δ(n−m)=x(m)δ(n−m)n=−∞∑∞x(n)δ(n−n0)=n=−∞∑∞x(n0)δ(n−n0)=x(n0)δ(n−n0)=x(n0)
因而又被称为单位样值信号。但是,应注意它与
δ(t)之间有重要区别,
δ(t)是广义函数,在
t=0时幅度趋向于无穷大,而
δ(n)在n=0处取值为有限值1。
任意一个序列,一般都可以用单位脉冲序列表示为
x(n)=k=−∞∑∞x(k)δ(k−n)
- 单位阶跃序列
u(n)={10n≥0n<0
它是一个右边序列,如下图所示。
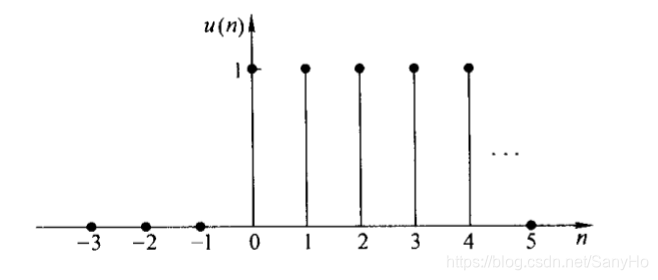
u(n)在n=0处有明确规定值1,这一点不同于
u(t)在
t=0处的取值。此外,经常将
u(n)与其它序列相乘,构成一个因果性序列。
单位阶跃序列
u(n)与单位脉冲序列
δ(n)之间有如下关系:
δ(n)=u(n)−u(n−1)u(n)=k=0∑∞δ(n−k)
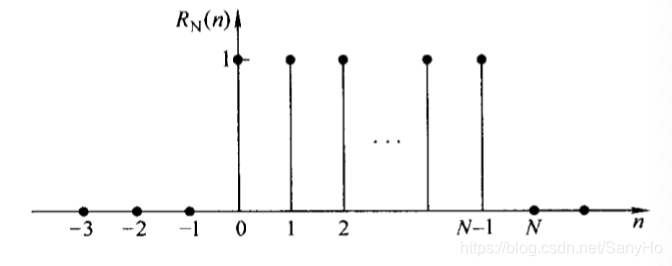
- 矩形序列
RN(n)={100≤n≤N−1其它
如下图所示,此序列从0到N-1,共有N个为1的数值,当然也可用
RN(n-m)表示从m到
m+N−1个为1的数值。如果用单位阶跃序列表示矩形序列,则有
RN(n)=u(n)−u(n−N)
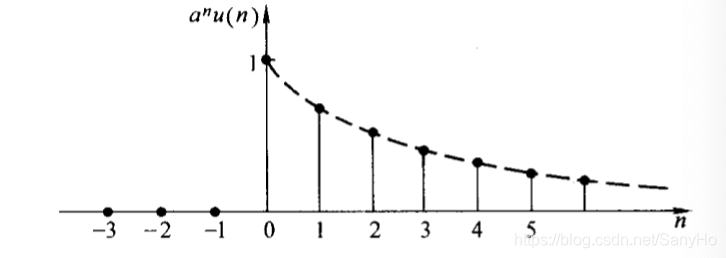
- 实指数序列
x(n)=anu(n)
它是单边指数序列,其中a为常数。当
∣a∣<1时,序列收敛;
∣a∣>1时,序列发散。
a>0时,序列都取正值;
a<0时,序列正负摆动。下图表示了
0<a<1时的情况。
- 正弦型序列
正弦型序列可理解为从连续时间正弦信号经采样得到,即
x(n)=Asin(wt+φ0)∣t=nT=Asin(nwT+φ0)=Asin(nΩ+φ0)
式中,A是幅度;T为采样周期;
Ω=wT表示离散域的角频率,称为数字角频率,单位为弧度(rad);
φ0为正弦序列的初始相角。
值得注意的是,连续时间正弦信号一定是周期信号,其周期为
T0=w2π,经采样离散化后的正弦序列就不一定是周期性序列,只有满足某些条件时,它才是周期性序列。
由于
x(n+N)=Asin[(n+N)Ω+φ0]=Asin(nΩ+NΩ+φ0)
若
NΩ=2πk,k为整数
则上式成为
Asin(nΩ+2πk+φ0)=Asin(nΩ+φ0)=x(n)
此时正弦序列是周期序列,其周期为
N=(Ω2π)k
k的取值使得
N=Ω2kπ为最小正整数,此时正弦序列是以N为周期的正弦型序列。下图表示周期N=12的余弦序列。
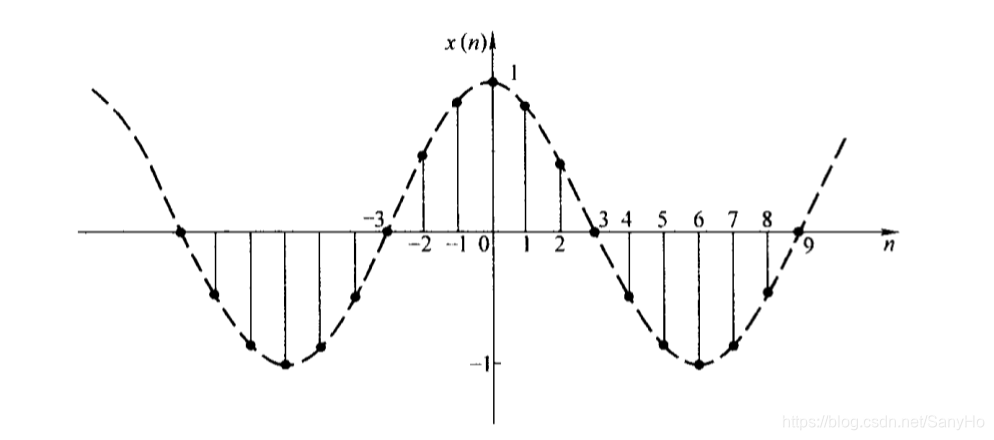
若
Ω2π=PQ=有理数(这里的Q、P为互为素数的整数),此时要使
N=Ω2πk=PQk为最小正整数,只有
k=p,所以周期
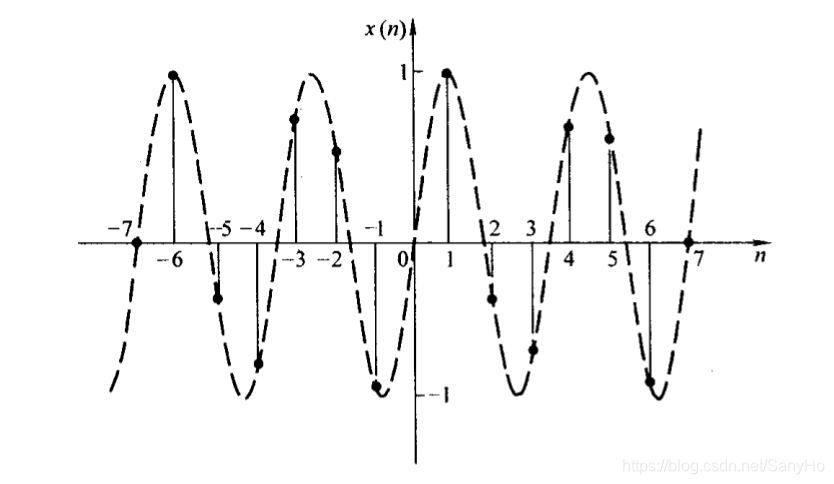
N=Q>Ω2π。下图表示了
Ω2π=27,周期N=7时的正弦序列。
若
Ω2π为一无理数,则任何k值都不能满足N为正整数,此时正弦序列就不可能是周期性序列。
- 复指数序列
复指数序列表示为
x(n)=e(σ+jΩ)n=eσn(cosΩn+jsinΩn)
当
σ=0时,复指数序列
ejΩn和正弦型序列一样,只有当
Ω2π为整数或有理数时,才是周期性序列。复指数序列
ejΩn和时域连续信号的复指数信号
ejwt一样,在信号分析中扮演重要角色。
比较连续正弦型信号
coswt(复指数信号
ejwt)和正弦型序列
cosΩn(复指数序列
ejΩn),除了连续正弦型信号(复指数信号)一定是周期信号,正弦型序列(复指数序列)不一定周期性序列外,信号频率取值范围的变化也特别值得注意。对于连续时间信号而言,其频率值
w可以在
−∞<w<∞区间任意取值,而对离散时间信号来说,由于
ej(Ω±2kπ)n=ejΩne±j2knπ=ejΩn(k为正整数)
表明正弦型序列(复指数序列)作为
Ω的函数是以
2π为周期的,换言之,离散信号的数字频率的有效取值范围是
0≤Ω≤2π或
−π≤Ω≤π。由此可见,经过采样周期为T的离散化后,使原来连续信号所具有的无限频率范围映射到离散信号的有限频率范围
2π。这一基本结论对任意信号都是适用的,所以在离散信号和数字系统的频域分析时,数字频率
Ω的取值范围为
0<Ω≤2π或
−π<Ω≤π。