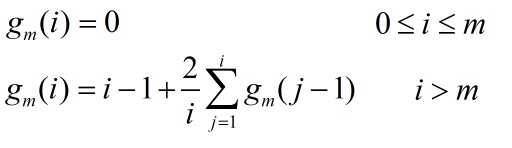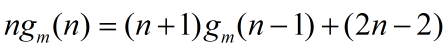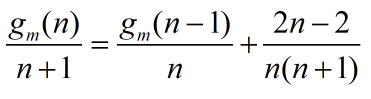ACM数列相关

写在前面

按理来说，求数列通项本应该属于数学范围，但ACM中也有数列推导题的出现，处于方便，笔者决定把一些常见数列整理出来。
注:笔者是一名十八线蒟蒻，如果有错误请在评论区下留言，谢谢您帮助我做得更好。

前置知识

无！带上你的小脑瓜跟着学就是了！

一、基础数列（等比、等差、等比*等差，累加，累乘）

众所周知，
(1)对于 $a_n=a_{n-1}+d(n\geq2)$,我们有
$a_n=a_1+(n-1)d,$ $S_n=na_1+\frac{n(n-1)}{2}d。$
(2)对于 $a_n=a_{n-1}*q(n\geq2)$，我们有
$a_n=a_1*q^{n-1}$
$S_n= \begin{cases} na_1, q=1\\ \frac{a_1*(1-q^n)}{1-q}, q≠1 \end{cases}$
(3)对于 $a_n$的通项是类似 $(an+b)q^{n}$这种"一个等差×一个等比"时，求 $S_n$可以通过错位相减法。操作略
(4)对于形如 $a_n=a_{n-1}+f(n)$的，我们可以通过构造式子的办法。
即构造
$a_n=a_{n-1}+f(n)$
$a_{n-1}=a_{n-2}+f(n-1)$
$a_{n-2}=a_{n-3}+f(n-2)$
…
$a_{2}=a_{1}+f(2)$
把上述所有式子加起来，化简消去，得到
$a_n=a_1+\sum^{n}_{i=2}f(i)$
(5)对于形如 $a_n=a_{n-1}*f(n)$的，也是构造式子
$a_n=a_{n-1}*f(n)$
$a_{n-1}=a_{n-2}*f(n-1)$
$a_{n-2}=a_{n-3}*f(n-2)$
…
$a_{2}=a_{1}*f(2)$
全部乘起来，化简，得到
$a_n=a_1*\prod^{n}_{i=2}f(i)$
（以上为高中生必备技能，请各位复习/预习一下）
(4)和(5)中的累加和累乘的方法很重要！
最后介绍一些常用公式。

$1+2+3+...+n=\frac{n(n+1)}{2}$
$1^2+2^2+3^2+...n^2=\frac{n(n+1)(2n+1)}{6}$
$1^3+2^3+3^3...+n^3=(\frac{n(n+1)}{2})^2$

Q：如何求解 $1^k+2^k+3^k+...+n^k$?
A：有个前提，k阶之前的次幂和公式必须是已知的。
先写出 $n^{k+1}-(n-1)^{k+1}$的展开式，即
$n^{k+1}-(n-1)^{k+1}=a_{k+1}n^k+a_kn^{k-1}+...+a_{0}$
我们构造式子，得到
$(n-1)^{k+1}-(n-2)^{k+1}=a_{k+1}(n-1)^k+a_k(n-1)^{k-1}+...+a_{0}$
$(n-2)^{k+1}-(n-3)^{k+1}=a_{k+1}(n-2)^k+a_k(n-2)^{k-1}+...+a_{0}$
…
$(2)^{k+1}-(1)^{k+1}=a_{k+1}(1)^k+a_2(n-1)^{1}+...+a_{0}$
全部累加，得到
$n^{k+1}=a_{k+1}\sum_{i=1}^{n}i^k+a_{k}\sum_{i=1}^{n}i^{k-1}+...$
因为k阶之前的公式是已知的，故就可求得 $\sum_{i=1}^{n}i^k$。
UPD(2020/2/13):可以通过伯努利数求解，效率更高。

（6）当然还有裂项相消啊之类的破玩意儿就不说了，遇到了就见仁见智。

二、一阶线性递推（形如 $a_n=pa_{n-1}+q$）

对于 $a_n=pa_{n-1}+q(n\geq2)$，我们先想办法消去这个系数 $q$然后转化为等比数列求解。
$p=1$时，同等差数列处理，接下来讲 $p≠1$的情况。
即设 $b_n=a_n-k$，且想办法让原式变为 $b_n=pb_{n-1}$。而 $p$已知， $b_1$可以算，那我们就能求出 $b_n$，进而求出 $a_n$。
$a_n-k=p(a_{n-1}-k)$
$a_n=pa_{n-1}+k-pk$
即: $k-pk=q$
$k=\frac{q}{1-p}$。
故 $b_1=a_1-\frac{q}{1-p}$, $b_n=(a_1-\frac{q}{1-p})*p^{n-1}$
所以我们得到 $a_n=(a_1-\frac{q}{1-p})*p^{n-1}+\frac{q}{1-p}。$

三、二阶线性递推（形如 $a_n=pa_{n-1}+qa_{n-2}+r$）

对于 $a_n=pa_{n-1}+qa_{n-2}+r(n\geq2)$我们根据之前求线递推性递推的思路，去考虑如何把二阶线性递推化为一阶线性递推。
我们设 $b_n=a_n-ka_{n-1}$，想办法使式子变为 $b_n=sb_{n-1}+r$，这样就可以用我们已经有的式子去求解。
将 $b_n=a_n-ka_{n-1}$代入，得到
$a_n-ka_{n-1}=s(a_{n-1}-ka_{n-2})+r$
$a_n=(s+k)a_{n-1}-ksa_{n-2}+r$
即 $s+k=p,-ks=q。$
这很容易联想到韦达定理，因此， $s,k$就是方程 $x^2-px-q=0$的两个解。
求出了 $s,k$后， $b_n$就能求，问题便能转化成 $a_n-ka_{n-1}=b_n$，累加即可。
这里不具体写过程，贴个结论。
对于 $a_n=pa_{n-1}+qa_{n-2}$。
如果该方程有二实根 $p,q$，则
$F(n)=Ap^n+Bq^n,A=\frac{F(2)-qF(1)}{p(p-q)},B=\frac{pF(1)-F(2)}{q(p-q)}$------------①
如果该方程只有一实根 $p$，则
$F(n)=(A+bn)p^n,A=\frac{pF(1)-F(2)}{p^2},B=\frac{F(2)-pF(1)}{p^2}$------------②
该方程无实根的情况我展示未遇到过…不知道虚数可不可以…
其实，对于更高阶的线性递推，都是用类似地方法，将 $n$阶降到 $n-1$阶的形式一层层降下去。
而这种方程的解，我们叫特征根(也叫不动点)。
对于一阶线性递推，其实 $\frac{q}{1-p}$就是特征根。
基本思路就是让方程分别减去特征根，然后化简，式子除一下。
而特征方程其实就是把所有的项（除了常数数）都变成 $x$，求出来的解就是特征根。

四、形如 $a_n=\frac{Aa_{n-1}+B}{C{a_{n-1}+D}}$

这种形式通常已经可以算是个毒瘤题了…
同样方法，先求特征根 $x=\frac{Ax+B}{Cx+D}$
（1）若该方程有两个特征根 $p,q$，则构造两个式子
$a_n-p=\frac{Aa_{n-1}+B}{C{a_{n-1}+D}}-p.........①$
$a_n-q=\frac{Aa_{n-1}+B}{C{a_{n-1}+D}}-q.........②$
然后令 $①÷②$，化简，可以得到类似之前的一个 $b_n=Kb_{n-1}$的形式，然后当成等比数列求就是了。
（2）若该方程只有一个特征根 $p$，则自构造一个式子
$\frac{1}{a_n-p}=\frac{1}{\frac{Aa_{n-1}+B}{C{a_{n-1}+D}}-p}$
然后化简，其他步骤同上。

五、递推方程中只有幂、乘除等运算

这个标题其实有点歧义的感觉，但一时又找不到很好的说辞…
这类问题主要是依靠一手套log
众所周知，我们有 $log$基本运算法则之：
$log(ab)=loga+logb$
$log(\frac{a}{b})=loga-logb$
$log(a^k)=kloga$
因此，一手log，可以让所有的幂运算、乘、除变成线性的简单运算，然后根据前文给出的内容去搞就完事了。
举个例子，对于 $a_n=a_{n-1}^2a_{n-2}$，两边套log，得
$loga_n=2loga_{n-1}+loga_{n-2}$
设 $b_n=loga_n$，
原式变为 $b_n=2b_{n-1}+b_{n-2}。$
再用二阶线性递推整个活即可。

六、方程中有 $\sum,\prod$的

举个例子，对于HDU 6680，其给出的数列如下

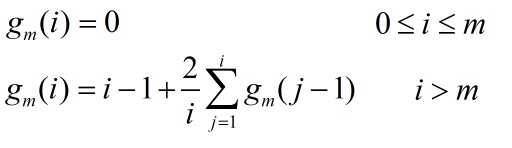
我们只需要构造 $g_m(i-1)$，然后令 $g_m(i)-g_m(i-1)$就能消去 $\sum$
对于 $\prod$，相除即可。

七、方程中的系数是非常数的

这类方程非常复杂，我这里主要讨论简单的。
还是这个HDU 6880为例，用上面的方法消去 $\sum$后，可以得到

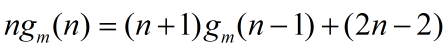
显然这个式子不满足我们上面说的任何一种情况，那咋整呢？
我们注意一个细节，项的下标 $n$与 $n-1$之差与其对应系数 $n$和 $n+1$之差相同。
那我们就两边同除以 $n(n+1)$，得到

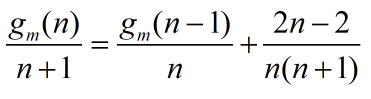
然后设 $b_n=\frac{g_m(n)}{n+1}$，就变成了
$b_n=b_{n-1}+\frac{2n-2}{n(n+1)}$，累加即可。右边的求和利用错位相减法得到。
类似地问题还可以是这个。
$(n+2)a_{n+1}=na_n+2(n+1)^{2r},r$是已知常数。（1992年中国台北数学奥林匹克试题） 
两边同乘 $(n+1)$得到
$(n+2)(n+1)a_{n+1}=n(n+1)a_n+2(n+1)^{2r+1}$。
记 $b_n=n(n+1)a_n$，得到
$b_n+1=b_n+2(n+1)^{2r+1}$。
后面部分是连续自然数求和，公式见之前的即可。
这一类问题其实很复杂，笔者也很难归纳出一般情况…

八、式子中存在组合数的

这里我们要用到一个性质： $C^n_m=C_n^{n-m}$
具体操作可以看我这篇博客… HDU 6467

九、式子中存在根号的

一般根号出现时，我们考虑三角换元或者代数换元，
eg1:求 $a_{n+1}=\frac{1}{16}(1+4a_n+\sqrt{1+24a_n}),a_1=1$（1981年第22届IMO预选题）
我们可以先用特征根的办法求一下，得到 $x_1=\frac{1}{3},x_2=0$
我们试着让两边减去 $\frac{1}{3}$,整理，得到
$48a_{n+1}=12a_n+3\sqrt{1+24a_n}-13$
很好，摸不着头绪了，此时似乎特征根的方法不管用。
那我们就试着换元。
记 $b_n=\sqrt{1+24a_n}$，那 $a_n=\frac{1}{24}(b_n^2-1)$
原式等价于 $\frac{1}{24}(b_{n+1}^2-1)=\frac{1}{16}(1+\frac{1}{6}(b_n^2-1)+b_n)$
化简，得到 $4b_{n+1}^2=b_n^2+6b_n+9$
即 $(2b_{n+1})^2=(b_n+3)^2$
而且因为 $b_n\geq0$，所以 $2b_{n+1}=b_n+3$。
一阶线性递推套一下，莽就完事了。

eg2:求 $a_n=\frac{\sqrt{1+a_{n-1}^2}-1}{a_{n-1}},a_0=1$（1990年匈牙利数学奥林匹克试题）
这题我们考虑三角代换。
熟练掌握三角代换的前提是：你要对三角公式（这里指半角/二倍角、万能公式、三倍角以及六个三角函数的倒数、商数和三个平方关系）相当熟练。
而且，通常我们有以下两个换元规则。
（1）根号里的数字比1大，我们采用 $tan,csc,sec$。（前者居多）
（2）根号里的数字比1小，我们采用 $sin,cos,cot$（前两者居多）
这题我们考虑设 $a_n=tanb_n(b_n∈(0,\frac{π}{2}))$
（为啥不是把根号换元？你根号换元了左边怎么办？ ）
于是原式等于
$tanb_{n+1}=\frac{\sqrt{tanb_n^2+1}-1}{tanb_n}$
$tanb_{n+1}=\frac{1-cosb_n}{sinb_n}=tan\frac{b_n}{2}$
$tanb_{n+1}=tan\frac{b_n}{2}$
因为 $tan$函数在 $(0,\frac{π}{2})$上单调递增，故 $2b_{n+1}=b_{n}$
莽就完事了。

后记

望2020的打铁生涯一切顺利…
(铜牌来一个好吗？秋梨膏)
DrGilbert 2020.2.5