概率论：均值、标准差、方差、协方差、矩

一、均值

1.1 离散情况：

$\overline{X}={\sum_{i=1}^nX_i\over n}$

二、标准差

$S=\sqrt{{\sum_{i=1}^n(x_i-\overline{X})^2\over n-1}}$

三、方差

1.1 样本方差：

$S^2={\sum_{i=1}^n(x_i-\overline{X})^2\over n-1}$

1.2 均值的方差

$D(\overline{x})=D({1\over n}\sum x_i)={1\over n^2}\sum D(x_i)={1\over n^2}\centerdot n\sigma^2={\sigma^2\over n}$

1.3 方差的性质

设C为常数， $D(C)=0$
设X是随机变量，C是常数，则有： $D(CX)=C^2D(X),D(X+C)=D(X)$
设X与Y是两个随机变量，则： $D(X\pm Y)=D(X)+D(Y)\pm2Cov(X,Y)$

四、协方差

4.1 为什么需要协方差

4.1.1 定义

标准差和方差一般是用来描述一维数据的，但现实生活中我们常常会遇到含有多维数据的数据集。最简单的是上学时我们要统计多个学科的考试成绩，面对这样的数据集，我们当然可以按照每一维独立的计算其方差，但是我们想了解的更多，比如数学成绩和物理成绩是不是有一定的相关关系，协方差就是这样一种用来度量两个随机变量关系的统计量。
我们可以仿照方差的定义：
$var(X)={\sum_{i=1}^n(X_i-\overline{X})(X_i-\overline{X})\over n-1}$
来定义协方差如下（离散）：
$cov(X,Y)={\sum_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})\over n-1}=E(xy)-E(x)E(y)$

协方差的结果如果为正值，则说明两者是正相关的（从协方差可以引出“相关系数”的定义）；如果结果为负值，则说明两者是负相关；如果为0，则说明两者之间没有关系，就是统计上的“相互独立”。

从协方差的定义上可以看出一些显而易见的性质，如：

$cov(X,X)=var(X)$
$cov(X,Y)=cov(Y,X)$

4.1.2 关于协方差的图解：

首先将x，y做去均值处理，此时 $\overline{x}=\overline{y}=0$ ，所以此时x和y之间的协方差：
$cov[x,y]=E[(x-\overline{x})(y-\overline{y})]=E[x\centerdot y]$

如果x和y的联合分布多位于一三象限，则 $x\centerdot y$ 多为正数，此时协方差为正，x和y正相关：
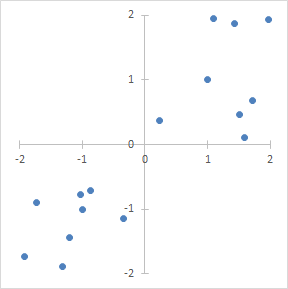
如果x和y的联合分布多分布在二四象限，此时 $x\centerdot y$ 多为负数，则协方差为负，x和y负相关
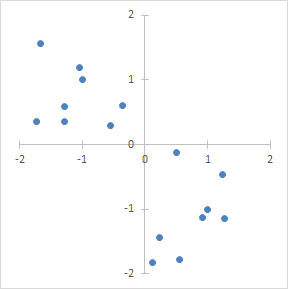
如果x和y几乎均匀的分布在所有象限中，则 $x\centerdot y$ 有正有负，均值接近于0，说明x和y之间没有相关性（只是说明没有线性相关）：

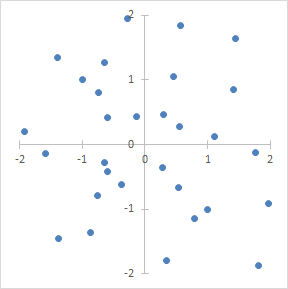
4.1.3 协方差的性质

$Cov(X,Y)=Cov(Y,X)$
$Cov(aX,bY)=abCov(X,Y)$
$Cov(X_1+X_2,Y)=Cov(X_1,Y)+Cov(X_2,Y)$

4.2 协方差矩阵

前面提到的问题是典型的二维问题，而协方差也只能处理二维问题，维数多了自然就需要计算多个协方差，这时我们会想到利用矩阵来组织这些数据（协方差矩阵就是用来计算各维度之间的相关性）：

4.2.1 定义

将二维随机变量 $(X_1,X_2)$ 的四个二阶中心距
$c_{11}=E\{[X_1-E(X_1)]^2\}$
$c_{12}=E\{[X_1-E(X_1)][X_2-E(X_2)]\}$
$c_{21}=E\{[X_2-E(X_2)][X_1-E(X_1)]\}$
$c_{22}=E\{[X_2-E(X_2)]^2\}$
排成矩阵的形式：
$\begin {pmatrix} c_{11}&c_{12}\\c_{21}&c_{22} \end {pmatrix}$
称此矩阵为 $(X_1,X_2)$ 的协方差矩阵

类似定义n维随机变量 $(X_1,X_2,...,X_n)$ 的协方差矩阵：
若：
$c_{ij}=Cov(X_i,X_j)=E\{[X_i-E(X_i)][X_j-E(X_j)]\}\quad i,j=1,2,...,n$
都存在，称矩阵：
$C=\begin {pmatrix} c_{11}&c_{12} &\dots &c_{1n}\\ c_{21}&c_{22}&\dots &c_{2n}\\ \vdots &\vdots&\ddots&\vdots\\ c_{n1}&c_{n2}&\dots &c_{nn} \end {pmatrix}$
为 $(X_1,X_2,...,X_n)$ 的协方差矩阵

4.2.2 性质

协方差矩阵是半正定矩阵
证明：
一组随机变量，共n个：
$X=(X_1,X_2,...,X_n)^T$
$设协方差矩阵为\varSigma,对任意向量y：$
$y^T\varSigma y=y^TE[(X-\mu)(X-\mu)^T]y$
$\quad\quad=E[y^T(X-\mu)(X-\mu)^T)y]$
$\quad\quad=E[((X-\mu)^Ty)^T((X-\mu)^T)y)]$
$\quad\quad=E[||(X-\mu)^Ty||^2]\ge0$

协方差矩阵是实对称矩阵

五、矩

5.1 混合矩和混合中心矩

设X和Y是随机变量
若：
$E(X^kY^L)\quad K,L=1,2,...$
存在，则称它为X和Y的K+L阶混合（原点）矩，
若：
$E{\{[X-E(X)]^k[Y-E(Y)]^k\}}$
存在，则称它为X和Y的K+L阶混合中心矩。
可以知道协方差cov（X，Y）是X和Y的二阶混合中心矩。