JZOJ7月17日提高组T1 亲戚

题目

Description

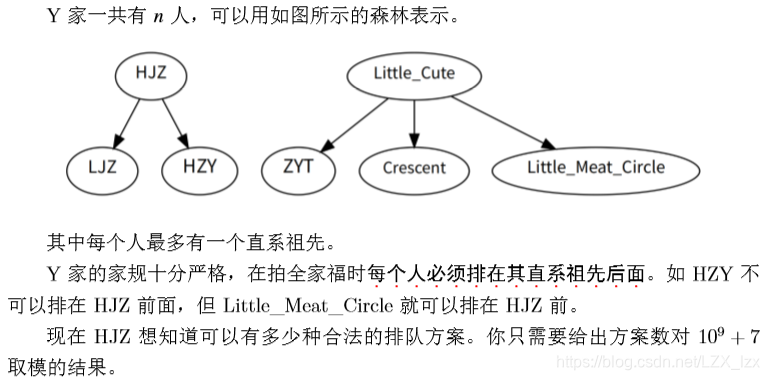
Input

Output

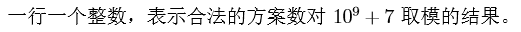
Sample Input

4
0 1 1 0

Sample Output

8

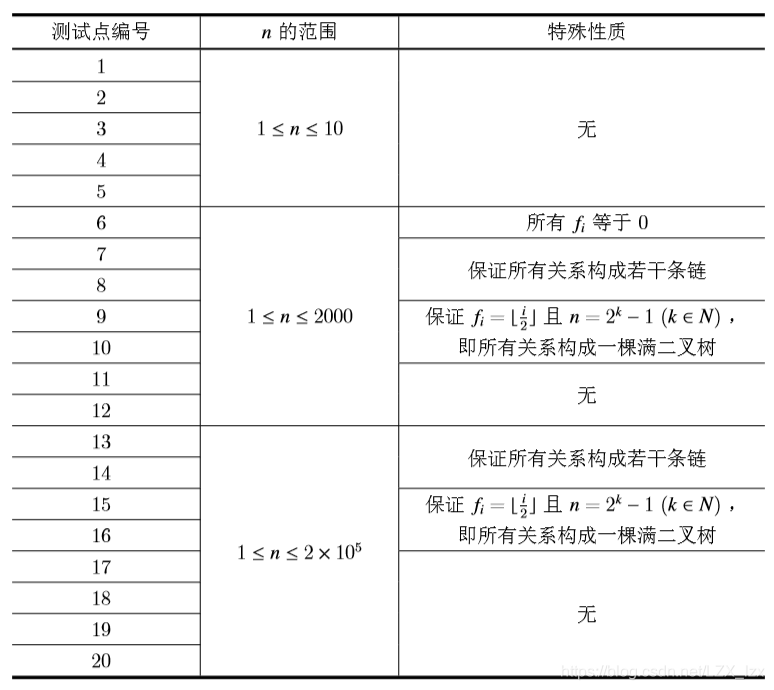
Data Constraint

题解

分析

题意：排序，其中每个节点必须在它的父亲之后

方法1

设一个虚拟根（如0）
使数据变成一棵树
先思考倒数第2层
那么这时候，不考虑当前节点
子节点的排序方法可以这样算：
当一个子节点进来时
判断是否为第一个子节点
如果不是，那么这个子节点就可以插入在已经进来的所有子节点的左右两侧
如图：

接下来思考剩下层
对于倒数第3层
这时以当前节点为根的树就不止一个节点了
那么这时候，就要用到组合数
设已经进入的儿子节点贡献的节点个数为 $num[now]$，将要进来的节点个数为 $num[x]$，那么有公式： $f[now]=C^{num[x]}_{num[now]+num[x]}*f[x]（f[now]表示当前节点合法的方案数，x是now的儿子节点）$
对于组合数，可以通过逆元来计算
我们知道： $C^x_y=\dfrac{x!} {y!*(x-y)!}$
PS：先预处理出阶乘
计算 $\dfrac{x!}{y!(x-y)!}$，如果暴力计算C++没有类型存的下（如果暴力模数可能会导致答案出错）
那么这时逆元就可以用起来了
求逆元有很多种方法
例如：费马小定理

---

以下是费马小定理如何求逆元：
我们知道，当 $a*x≡1(mod$ $P)$时，称 $x$是 $a$在模 $P$下的逆元（反过来也行）
同时又有费马小定理：当 $P$是质数时，有 $a^{P-1}≡1(mod$ $P)$，而且显而易见 $a^{P-1}=a*a^{P-2}$
所以 $a^{P-1}≡1(mod$ $P)$可以转换为 $a*a^{P-2}≡1(mod$ $P)$
结合 $a*x≡1(mod$ $P)$和 $a*a^{P-2}≡1(mod$ $P)$，可以发现
在模 $P$的意义下时， $a^{P-2}$就是 $a$的逆元
而 $a^{P-2}$通常用快速幂来求
注意，费马小定理推逆元仅当P是质数时才适用！！！

---

求出组合数后，依次传递
最后输出 $f[0]$
结合代码理解

方法2

对于答案，其实有公式： $ans=\dfrac {n!} {\prod _{i=1}^{n}Size_i}$
其中 $Size_i$表示以i为根节点的子树的点的个数
为什么呢？
证明过程：

Code（方法1）

#include<cstdio>
#define mod 1000000007
using namespace std;
int n,i,x,tot,num[200005];
long long f[200005],jc[200005];
struct node
{
	int to,head,next;
}a[200005];
long long ksm(long long x,long long y)
{
	long long s;
	s=1;
	while (y>0)
	{
		if (y&1) s=s*x%mod;
		y>>=1;
		x=x*x%mod;
	}
	return s;
}
long long Cc(int x,int y)
{
	long long Ksm=ksm(jc[y]*jc[x-y]%mod,mod-2)%mod;
	long long ccc=jc[x]*Ksm%mod;
	return ccc%mod;
}
void dfs(int now)
{
	int i,x;
	long long c;
	for (i=a[now].head;i!=0;i=a[i].next)
	{
		x=a[i].to;
		dfs(x);
		if (num[now]!=0)
		{
			c=Cc(num[now]+num[x],num[x]);
			f[now]=f[now]*c%mod;
		}
		num[now]+=num[x];
		f[now]=f[now]*f[x]%mod;
	}
	num[now]++;
}
int main()
{
	freopen("input.in","r",stdin);
	scanf("%d",&n);
	f[0]=1;
	for (i=1;i<=n;i++)
	{
		scanf("%d",&x);
		tot++;
		a[tot].to=i;
		a[tot].next=a[x].head;
		a[x].head=tot;
		f[i]=1;
	}
	jc[0]=1;
	for (i=1;i<=n;i++)
		jc[i]=jc[i-1]*(long long)i%mod;
	dfs(0);
	printf("%lld\n",f[0]);
	return 0;
}

抱歉只有方法1的Code，毕竟方法2的代码量很小，可以自己试着理解码出来