投资的收益和风险
符号规定:
si表示第i种投资项目,s0为存入银行
ri表示平均收益率
pi表示交易费率
qi表示风险损失率
ui表示交易定额
xi表示项目资金
a表示投资风险度
Q表示总体收益
M投资数额
模型建立:
总体风险用所投资的si中最大的一个风险来衡量,即
Max{qixi|i=1,2,…,n}
购买所需的交易费是一个分段函数即
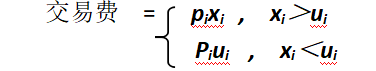
而题目所给的定值ui相对总投资M很小,piui相对pixi小,这样净收益为(ri-pi)xi
要使净收益尽可能打,总体风险尽可能小,这是一个多目标规划模型
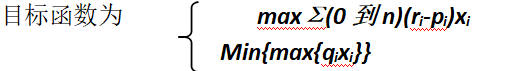
在保证收益大的同时,将风险最高的的风险保证到最低(有点绕口诶)
约束条件为 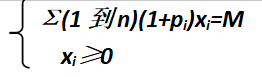
模型简化:
1 若给定风险界限a,则 qixi/m≤a,可以此进行线性规划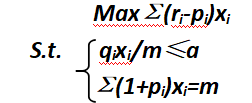
可以根据a和所对应的风险度画出图来进行比较(hold on +while 循环来画)
关于写的程序中,将每个xi分开列,并且将linprog中的b赋值为a*zeros()的形式,通过a的不断变化循环,每次变化所得的结果利用hold on 以a为x轴,以q为y轴来作图来画图,通过图像比较得出结论。
整数规划
数学规划中的变量(部分或全部)限制为整数时,称为整数规划。若在线性规划模型中,变量限制为整数,则称为整数线性规划。目前所有流行的求解整数规划的方法,往往只用于整数线性规划。目前还没有一种方法能有效地求解一切的整数规划
分类
变量全限制为整数时,称纯(完全)整数规划
部分限制为整数时,称混合整数规划
特点
原线性规划有最优解,当自变量限制为整数后,其整数规划解出现下述情况。
1原线性规划最优解全是整数,则整数规划最优解与线性规划最优解一致
2整数规划无可行解
求解方法分类:
分枝定界法——可求纯或者混合整数线性规划
割平面法——可求纯或混合整数线性规划
隐枚举法——求解“0—1”整数规划
1过滤隐枚举法
2分枝隐枚举法
匈牙利法——解决指派问题(“0-1”规划特殊情况)
蒙特卡洛法——求解各种类型规划
0-1型整数规划
0-1型整数规划是整数规划中的特殊情况,他的变量xj仅取值0或1.这时xj称为0-1变量,或称二进制变量。xj仅取值0或1这个条件可由下述约束条件
0≤xj≤1且xj为整数所替代
可以将互相排斥的约束条件转化为普通的约束条件
例如:x1=0 或500≤x1≤800
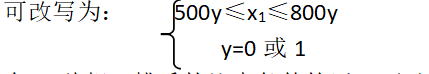
如果有m种相互排斥的约束条件的话,可以增加一个Σyi=1来限制
关于固定费用的问题
加入由三种投资方式,投资不同所得到的产量也不同,要求出最小成本。
首先,各种生产方式所需要的总成本为: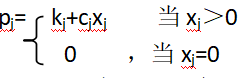
而在构造函数的时候,再分类讨论就太过复杂,注意pi是否为0是由xj决定的,而当xj为0时,上式和下式的差别只是上式多了一个kj,所以,只需要给kj前边加一个0-1变量(由xj决定),就可以将三组变量写进一个式子。
相应地,约束条件也应该加入这个0-1变量。
指派问题的数学模型
派n个人去做n项工作,每个人做且仅做一项工作,若分配第i个人去做第j项工作,需花费cij的时间,怎样分配才会使时间最短
要给出指派问题的实例,只需给出矩阵C=(Cij),C称为指派问题的系数矩阵
引入0-1变量xij(做该项工作为1不做为0)
数学模型:minΣΣcijxij,
蒙特卡洛法(随机取样法)
1.求面积的近似值:先选取一个比较好算的区域,(包括了目标函数),再制造随机分布的点(数量够大),通过计算落在目标区间内的点的数量和总数之比来估算面积
先放程序:
clc,clear
X=unifrnd(0,12,[1,10000000]);
Y=unifrnd(0,9,[1,10000000]);
Pinshu=sum(y<x.^2&x<=3)+sum(y<12-x&x>=3);
Area=129pinshu/10^7;
题目就不放了因为主要想讲的并不是题目,而且看出来也不用费多大的功夫,先谈谈我对这个程序的感受吧
首先他并不是在平面直角坐标系中构造点,而是将二维问题来一维解决,也就是说他并不是按他的思路那样在图上撒点,而是将图上的约束条件化为线性条件,x和y可以看成横坐标和纵坐标,也可以看成俩个不相干的变量
非线性整数规划以后再看
整数线性规划的计算机求解
Matlab中用intlinprog来求解整数的线性规划,但是必须把所有的决策向量一维化,和第一篇文章的那个很像,可以参考那个看
intlinprog和linprog的区别在于intlinprog的格式在f后面加了一个intcoin,而intcoin则决定了第几个未知量为整数。