划分[CSP2019D2T2][单调队列]

题目

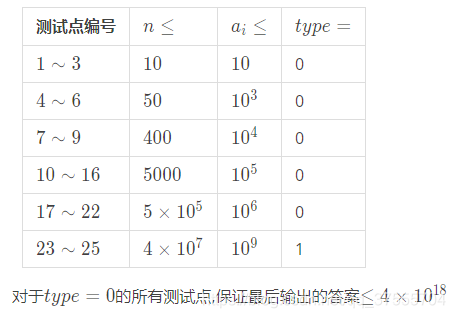
一个长度为 $n$ 的数组 $a$ ，从左到右分段，记第 $i$ 段和为 , $s_i=\sum_{j=l_i}^{r_i}a_i$ ，要求 $s_{i-1}\le s_i\ (i>1)$ ,记权值和 $W=\sum s_i^2$，求 $W_{min}$

部分分做法

$12opt$

枚举分段点然后检验
时间复杂度 $O(2^nn)$

$24opt$

可以各种 $Dp$ ，主要是水篇幅
$f_{i,j}：$ 前 $i$ 个数，最后一段的和为 $j$ 目前最小和
$f_{i,j}=min\{f_{k,q}+j^2\}(j=s_i-s_k)$
暴力枚举 $O(n^2m^2)$ 再注意一下范围卡卡常

$36opt$

$f_{i,j}$ 前 $i$ 个数，最后一段为 $(j,i]$ 的目前最小和
$f_{i,j}=min\{f_{j,k}+(s_i-s_j)^2\}$ $s_j-s_k\le s_i-s_j$
$O(n^3)$

---

我们可以尝试对 $24opt$ 的枚举进行优化
$f_{i,j}=min\{f_{k,q}+j^2\}(j=s_i-s_k)$

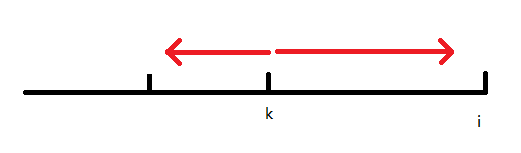
先枚举 $k$ ，再向两边同时拓展，并且记录 $f_{k,q}$ 最小值
时间复杂度 $O(n^2m)$

$64opt$

$f_{i,j}=min\{f_{j,k}+(s_i-s_j)^2\}$ $s_j-s_k\le s_i-s_j$
同样的优化方法优化 $O(n^3)$ 得到 $O(n^2)$
开始扯结论
根据 $n$ 元均值不等式可得：
$\frac{x_1+...+x_n}{n}\le \sqrt{\frac{\sum_{i=1}^nx_i^2}{n}}$
也就是
$\frac{s^2}{n}\le W$
当 $x_1=x_2=...=x_n$ 时候取等号
那么分的越平均越优秀
一种调整方法：
设 $x_a<x_b<x_c<x_d$ 并且 $x_a+x_d=x_b+x_c$ ，那么 $x_b^2+x_c^2\le x_a^2+x_d^2$
意味着相邻两段可以通过调整使得值优秀一点

然后就会使相邻的又有机会调整

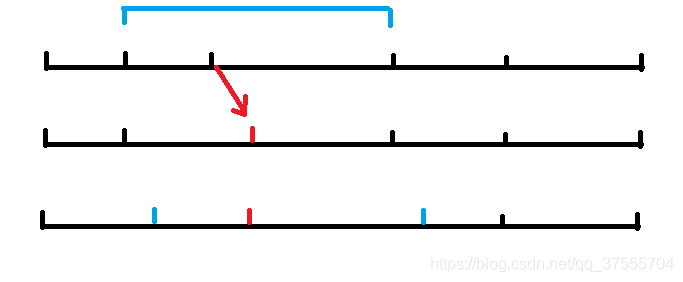
以此类推，最终调整不行时候就是最优解
那么此时显然有最后一段的划分点离右端点最近
那么尝试有关 $dp$ 决策点的优化

$85opt\sim 100opt$

定义 $f_{i}$ 为 $i$ 的最优决策点，那么类似 $O(n^2)$ 的有
枚举 $i$ 的决策点 $j$ 来更新 $f_i$
$S_{j}-S_{f_j}\le S_i-S_{j}$
移项可得 $2*S_{j}-S_{f_j}\le S_i$
发现右边是只和决策点 $j$ 相关的代数式记为 $g_j=2*S_{j}-S_{f_j}$
$g_j$ 肯定越小越好
考虑两个决策点 $k<j$ 并且 $g_k>g_j$ 那么永远只会选择 $j$
也就是可以考虑维护一个单调递增的栈，然后用 $S_i$ 去二分
然后发现 $S_i$ 也有单调性就可以做到 $O(n)$