子串周期查询问题的相关算法及其应用
南京外国语学校 陈孙立
摘 要
本文介绍了子串周期查询问题的解决方法, 以及解决这个问题所使用的到的一些结论和字符串工具——基本子串字典 (Dictionary of Basic Factors) , 接着介绍了前述结论和工具的一些应用.
-
本文第二节引入了一些基础定义和记号.
-
本文第三节证明了三个重要引理, 引入基本子串字典.
-
本文第四节描述了解决子串周期查询问题的方法.
-
本文第五节介绍了基本子串字典的一些应用.
1 引言
现阶段计算机科学界对字符串的研究越来越注重于对周期, 即" 重复模式" 的性质的探究. 这一方向也具有很大的现实意义, 如语音识别、DNA 匹配等, 它们都需要对大量重复的字符串模式的精巧刻画.
子串周期查询问题是一个描述简单但是做法复杂的经典问题, 由此还可以延伸到应用更广的内部模式匹配 (Internal Pattern Matching) 问题. 本文着重介绍了它的解决办法, 以及一些扩展。
2 记号、基础定义与问题描述
2.1 记号与定义
令 \(S\) 为一个字符串, \(|S|\)为其长度, 记 \(S[i]\) 为 \(S\) 的第 \(i\) 个字符, \(S[l,r]\) 为把 \(S\) 的第 \(l\) 个字符到第 \(r\) 个字符取出组成的新字符串, 若 \(l>r\) 则 \(S[l,r]=\empty\).
记 \(\operatorname{pref}(S,x)=S[1\dotsb x]\) 为 \(S\) 的长度为 \(x\) 的前缀, 类似地, \(\operatorname{suf}(S,x)=S[|S|−x+1\dotsb|S|]\) 为 \(S\) 的长度为 \(x\) 的后缀.
若 \(T[x\dotsb x+|S|−1]=S\) , 我们说 \(S\) 在 \(T\) 中的 \(x\) 位置出现, \(x\) 是 \(S\) 在 \(T\) 中的出现位置或匹配位置.
定义 1: 若串 \(S\) 和整数 \(x\) 满足 \(1\leq x\leq |S|\) , 且对于所有的 \(1\leq i\leq |S|−x\) , 都有 \(S[i]=S[i+x]\) , 则称 \(x\) 为串 \(S\) 的周期或周期长度. 特别地, 若 \(x\) 还是 \(|S|\) 的因数, 则称 \(x\) 是 \(S\) 的整周期, 称 \(S\) 是整周期串.
显然, 若 \(x\) 是 \(S\) 的周期, 则 \(kx(k\in \Z^+,k\cdot|x|\leq |S|)\) 也是 \(S\) 的周期, \(x\) 也是 \(\operatorname{pref}(S,y),y\geq x\) 的周期。
定义 2: \(\operatorname{per}(S)\) 表示所有 \(S\) 的周期组成的集合, \(\operatorname{minper}(S)\) 表示 \(\operatorname{per}(S)\) 中的最小值. 不难发现对于非空串 \(S\) , \(|S|\) 一定是 \(S\) 的周期, 因此 \(|\operatorname{per}(S)|>0\).
定义 3: 若串 \(S\) 和整数 \(x\) 满足 \(0\leq x\leq |S|\) , 且满足 \(\operatorname{pref}(S,x)=\operatorname{suf}(S,x)\) , 则称 \(\operatorname{pref}(S,x)\) 是 \(S\) 的 \(\mathrm{border}\) .
推论 1: \(|S|−x\) 是 \(S\) 的周期当且仅当 \(\operatorname{pref}(S,x)\) 是 \(S\) 的 \(\mathrm{border}\) .
证明: 根据 \(\mathrm{border}\) 和字符串相等的定义可得: \(\operatorname{pref}(S,x)\) 是 \(S\) 的 \(\mathrm{border}\) 当且仅当对于所有的 \(1\leq i\leq |\operatorname{pref}(S,x)|\) 都有 \(\operatorname{pref}(S,x)[i]=\operatorname{suf}(S,x)[i]\) , 也即 \(S[i]=S[|S|−x+i]\) , 与周期的定义相符.
推论 2: 若 \(p\) 是 \(S\) 的周期, 且某个满足 \(r−l+1\geq p\) 的子串 \(S[l\dotsb r]\) 有周期 \(q\) , 并满足 \(q|p\) , 则 \(q\) 也是 \(S\) 的周期.
此推论比较显然.
2.2 问题描述
给定一个字符串 \(S\) , 以及若干次询问. 每个询问给出 \(l,r\) 两个数, 要求给出 \(\operatorname{per}(S[l\dotsb r])\) .
通过下文将要给出的结论, 可以用一种简洁的方式去表示 \(\operatorname{per}(S[l\dotsb r])\) , 花费 \(O(\log n)\)的空间, 而不是最坏情况下的 \(O(|S|)\) , 并且给出一个预处理需要 \(O(n\log n)\) 的时间与空间, 每次回答询问需要 \(O(\log n)\) 的时间与空间的算法.
3 解决问题的准备工作
3.1 关于“重复”的一些性质
关于字符串周期有一个重要的引理, 叫做 Periodicity Lemma. 它本身的证明比较繁琐, 下面我们证明它的弱化版本.
引理 1 (Weak Periodicity Lemma): 若 \(p,q\in\operatorname{per}(S)\) , 且 \(p+q\leq|S|\) , 则 \(\gcd(p,q)\in \operatorname{per}(S)\) .
证明:不妨假设 \(p<q\) . 对于任意 \(1\leq i\leq |S|\) , 若 \(p<i\leq|S|−q+p\) , 则 \(S[i]=S[i−p]=S[i+q−p]\) , 若 \(i≤p\) , 则 \(S[i]=S[i+q]=S[i+q−p]\) , 那么可得 \(q−p\) 也是 \(|S|\) 的周期. 这里用到了周期的定义和 \(p+q\leq|S|\) 的条件. 而又有 \(p+(q−p)\leq|S|\) , 所以可以用辗转相除法一直得到 \(\gcd(p,q)\) 是 \(|S|\) 的周期.
推论 3: 若 \(p=\operatorname{minper}(S)\leq\frac{|S|}{2}\) , 则对于任意 \(x\in \operatorname{per}(S),x+p\leq |S|\) , \(有 p|x\) .
证明:若 \(p\nmid x\) , 根据 引理 1 有 \(\gcd(p,x)\in \operatorname{per}(S)\) , 而 \(p<x\) , 所以 \(\gcd(p,x)<p\) , 与 \(p=\operatorname{minper}(S)\) 矛盾.
以下把 Weak Periodicity Lemma 简写为 WPL .
引理 2: 若串 \(S,T\) 满足 \(2|S|\geq|T|\) , 则 \(S\) 在 \(T\) 中的出现位置构成一个等差数列.
证明:若 \(S\) 在 \(T\) 中出现了一次或两次, 则引理已证完, 因此只需考虑 \(S\) 在 \(T\) 中至少出现了 \(3\) 次.
对于两次出现位置 \(p<q\) , 由于 \(S\) 是 \(T[p\dotsb q+|S|−1]\) 的 \(\mathrm{border}\), 有 \(q−p\) 是 \(T[p\dotsb q+|S|−1]\) 的周期. 同时根据 \(1\leq p,q\leq |T|−|S|+1\) , 有 \(p+|S|−1\geq |S|\geq |T|−|S|\geq q\) , 因此 \(q−p<|S|\) , 则 \(q−p\) 也是 \(S\) 的周期.
那么我们考虑 \(S\) 在 \(T\) 中的前两次出现位置 \(p_1<p_2\) 和某一次出现位置 \(q>p2\) , 有 \(p_2−p_1,q−p_2\in \operatorname{per}(S)\) . 又有 \(q−p_1\leq |T|−|S |\leq |S|\) , 根据 WPL 可得 \(r=\gcd(p_2−p_1,q−p_2)\in \operatorname{per}(S)\) . 同时, 可以发现 \(r\leq \min(p_2−p_1,q−p_2)\leq \frac{q−p_1}{2}\leq\frac{|S|}{2}\) . 令 \(r'=\operatorname{minper}(S)\) , 那么根据 推论 3 有 \(r'|r\) . 再根据 推论 2 , 得到 \(r'\) 是 \(T[p_1\dotsb p_2+|S|−1]\) 的周期. 假设 \(r'<r\) , 根据前面的结论, \(S\) 在 \(p_1+r'\) 位置同样出现, 和 \(p_2\) 是第二次出现位置矛盾. 因此 \(r=r'=\operatorname{minper}(S)\) .
至此, 再使用一次 推论 3 , 就可以得到 \(r|q−p_2\) . 另一方面, 若令 \(q\) 是 \(S\) 在 \(T\) 中的最后一次匹配位置, 则任何满足 \(x=p_1+kr\leq q,k\in Z\) 的 \(x\) , 根据上面的结论, 都是 \(S\) 的出现位置. 综合这两个结论, 就证明了 引理 2 .
不仅如此, 我们还得到了: 若 \(S\) 在 \(T\) 中至少出现三次, 则对应等差数列的公差为 \(\operatorname{minper}(S)\) .
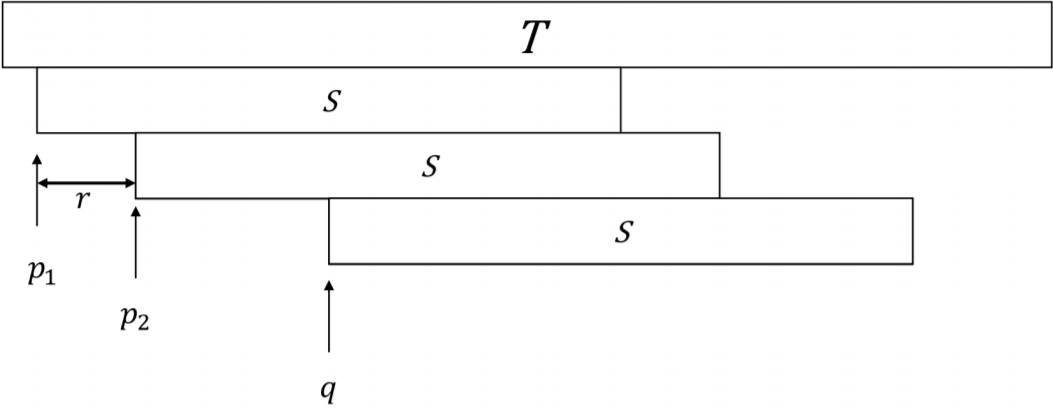
引理 3: 串 \(S\) 的所有不小于 \(\frac{|S|}{2}\) 的 \(\mathrm{border}\) 长度构成一个等差数列.
证明:只需证明 \(S\) 的所有不大于 \(\frac{|S|}{2}\) 的周期构成一个等差数列, 而这个结论可以由 推论 3 直接得到.
3.2 数据结构:基本子串字典
解决子串周期查询问题还需要一种被称为基本子串字典的数据结构。
定义 4: 一个串 \(S\) 的基本子串字典 (Dictionary of Basic Factors) , 称为 \(\operatorname{DBF}(S)\) , 它由 \(\lfloor \log_2|S|⌋+1\) 个数组组成. 具体地, 第 \(t\) 个数组用 \(Name_t\) 表示, 长度为 \(|S|−2^t+1\) , 满足 \(Name_t(i)≤Name_t(j)\) 当且仅当 \(S[i\dotsb i+2^t−1]\leq S[j\dotsb j+2^t−1]\) . 一般情况下, 可以再额外限制每个 \(Name_t\) 中的值为正整数, 且值域恰好为 \({1,2\dotsb k}\) , 其中 \(k\in \Z\).
不难发现, 数组 \(Name_t\) 可以由 \(Name_t−1\) 得到。因此要求出串 \(S\) 的基本子串字典, 直接使用类似 Manber & Myers 的倍增求后缀数组算法即可, 复杂度 \(O(n \log n)\).
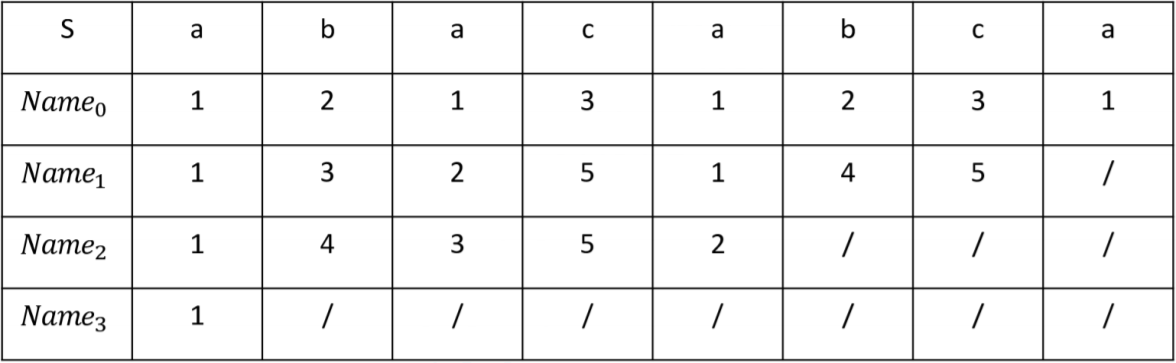
仅有 \(Name\) 数组可能还不够, 一个简单的扩展是把每个 \(Name_t\) 数组按值分开, 即对于每个 \(x\) 维护一个有序表, 记录 \(Name_t[i]=x\) 的所有的 \(i\) . 不难发现这一步也可以在构建基本子串字典的过程中完成, 复杂度依然是 \(O(n\log n)\) .
后面将会看到, 为了达到目前最优的一次查询 \(O(\log n)\) , 还要对基本子串字典的再次扩展.