数学建模之传染病SIR模型（新冠真实数据）

传染病模型的基本问题

• 描述传染病的传播过程
• 分析受感染人数的变化规律
• 预报传染病高潮到来的时刻
• 预防传染病蔓延的手段
• 按照传播过程的一般规律用机理分析方法建立模型

注：我们这里是介绍数学医学领域中基本的传染病模型。不从医学角度分析各种传染病的特殊机理，按照传播过程的规律建立微分方程模型.

建立模型

模型一

假设：

1. 设已知感染人数为 $i(t)$(病人数量随时间变化)
2. 设每个病人（单位时间）每天有效接触（足以使人治病）人数为 $\lambda$

模型：
单位时间 $\Delta{t}$内， $新增的人数（现有-原有）=原有的 \times \lambda$，即

$i(t+\Delta{t})-i(t)=\lambda i(t)\Delta{t}$
一开始的感染人数为 $i_0$
$i(0)=i_0$
解微分方程可以得到
$i(t)=i_0e^{\lambda t}$
所以可以可到当 $\lambda \rightarrow \infin$时 $i(t) \rightarrow \infin$
当然这是不可能的，因为我们考虑的因素太少了，首先一个是，若有效接触的是病人，则不能使病人数增加，所以必须区分已感染者(病人)和未感染者(健康人)看模型二来解决这个问题

模型二

假设：

1. 将人群分为两类：易感染者(Susceptible,健康人)和已感染者(Infective, 病人).
2. 总人数N不变，时刻t健康人和病人所占比例分别为 $s(t)$和 $i(t)$, 有 $s(t)+i(t)=1$
3. 每个病人每天有效接触人数为 $\lambda$(日接触率),且使接触的健康人致病.

建模：
每天新增的总人数为原有的人数乘以每个人可以传染的健康的人数，再乘 $\Delta t$

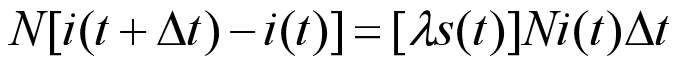
$\Delta t$除过去，两遍N约分得到下面，

MATLAB解一下这个微分方程

y=dsolve('Dy=n*y*(1-y)','t');

y =
 -1/(exp(C1 - n*t) - 1)
                      0
                      1

写规范点就是这个函数

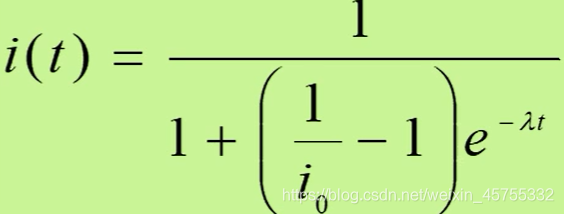
函数图像大致为

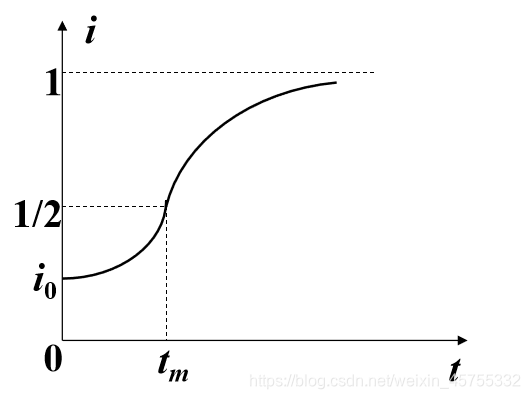
可以看出 $t=t_m$时这里图像的斜率有个最大值，其也就是传染的最快的时候，即传染病的高潮时刻，当然 $t_m$是可以求出来的

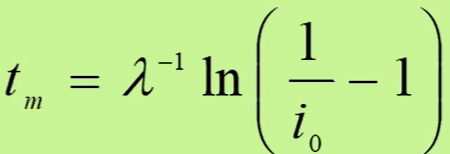
再看原式，当 $t\rightarrow \infin$时 $i\rightarrow 1$
病人的比例为1，当然这也是不可能的，因为我们还没有考虑有没有可能治愈，看模型三

模型三

假设：

1. 传染病无免疫性如伤风、痢疾等——病人治愈成为健康人，健康人可再次被感染。
2. 病人每天治愈的比例为 $\mu$ (日治愈率)， $\frac{1}{\mu}$为感染期，

模型
这是减去了治愈人数之后的新增人数


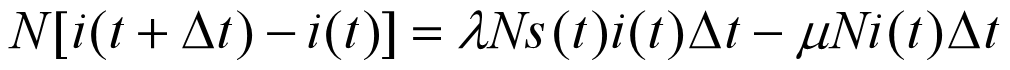
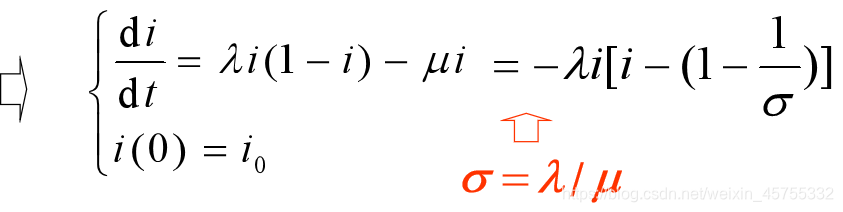
$\sigma$ 为一个感染期内每个病人的有效接触人数，称为接触数

可以画出上面的图形分析下

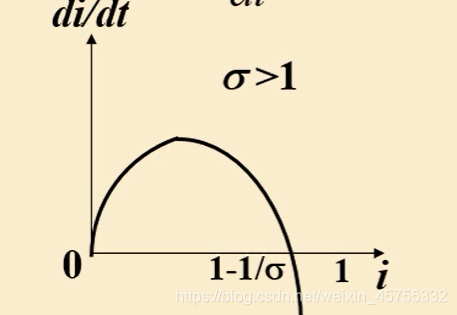
对上面的公式进行分析，可以得到，当 $i=1-\frac{1}{\sigma}$时， $i$对t的导数为0这也就到了 $i$的最大值；当 $0<i<1-\frac{1}{\sigma}$时， $di/dt<0$，i单调递增，且在 $di/dt$最大时，i的斜率最大，增速最快；当 $i>1-\frac{1}{\sigma}$， $di/dt<0$，i是单调递减的。

---

当然我们也可以画出 $i$随t的函数图像

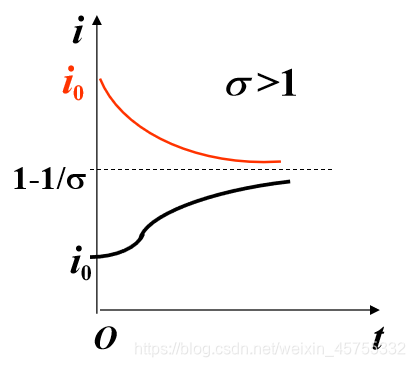
先看红线，若初始条件 $i_0>1-\frac{1}{\sigma}$ $di/dt<0$，i就是单调递减的，
若若初始条件 $i_0<1-\frac{1}{\sigma}$，i就是递增的，可以看到i对t的导数图像有一个最大值，下面的黑线就有一个增加速率最快的一个值，按S形曲线增长

---

$\sigma =<1$时 $di/dt<0$ i肯定是单调下降的，最终降到0

---

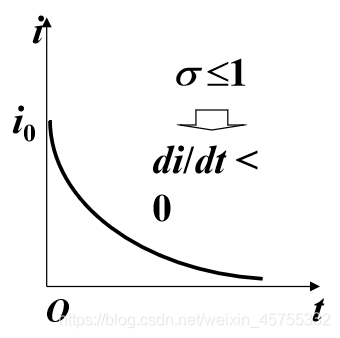
综上：
想让患病者越来越少， $\sigma$必须小于等于1，即感染期内有效接触使健康者感染的人数不超过原有的病人数.

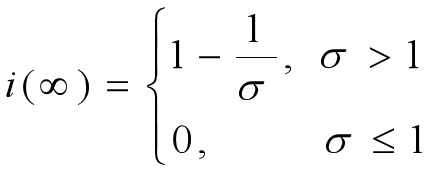
这里我们分析的是感染之后还能感染的情况，但有些病毒感染之后会在体内生成抗体，就不会再被感染了，下面我们分析这种情况。

模型四 SIR模型

SIR模型是常见的一种描述传染病传播的数学模型，其基本假设是将人群分为以下三类：

1 易感人群（Susceptible）：指未得病者，但缺乏免疫能力，与感病者接触后容易受到感染。

2 感染人群（Infective）：指染上传染病的人，他可以传播给易感人群。

3 移除人群（Removed）：被移出系统的人。因病愈（具有免疫力）或死亡的人。这部分人不再参与感染和被感染过程。

假设：

1. 传染病有免疫性如天花、麻疹等——病人治愈后移出感染系统，称移出者(Removed).
2. 总人数N不变，健康人、病人和移出者的比例分别为 $s(t), i(t), r(t)$.
3. 病人的日接触率为 $\lambda$ , 日治愈率为 $\mu$, 接触数 $\sigma=\frac{\lambda}{\mu}$

建模：
$s(t)+ i(t)+ r(t)=1$
这个就是病人减去治愈的人，和上一个模型是一样的

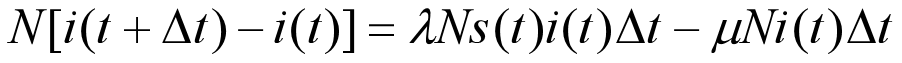
因为有治愈后是有免疫性的，所以可能被感染的总人数要减少，减去移除者就是

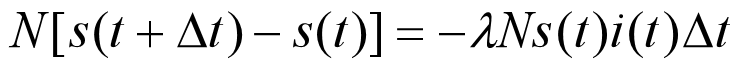
将上式化简为：

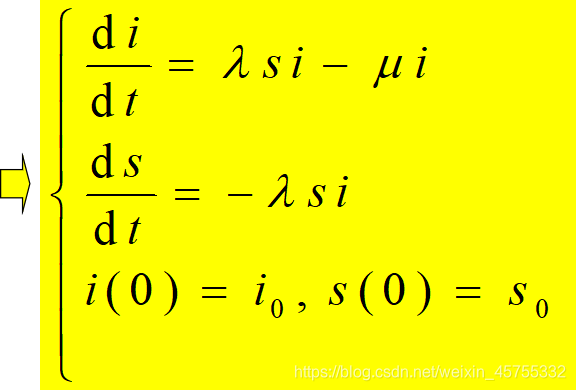
$i_0+s_0\approx 1$(通常 $r(0)=r_0$很小)

关于i(t) , s(t) 的非线性微分方程组，没有解析解，只能通过数值计算得到s(t), i(t), r(t)的曲线，下面来看下曲线的数值解的MATLAB程序

这里我们先设 $\lambda =1, \mu=0.5, i_0=0.01,s_0=0.99$
也就是平均一个病人人传染一个正常人，治愈率为0.5；开始的病人比例为0.01，正常人为0.99，设没有天生带有病毒抗体的人，所以 $r_0=0$，之后若果病人被治愈，则具有抗体了，有抗体的人为: $r=1-i-s$

ts=0:40;
x0=[0.01, 0.99];
[t,x]=ode45('ill',ts,x0);
r=1-x(:,1)-x(:,2);
plot(t,x(:,1),t,x(:,2),ts,r),grid
legend('i(t)','s(t)','r(t)')

function y=ill( t,x)
a=1;
b=0.5;
y=[a*x(1)*x(2)-b*x(1);-a*x(1)*x(2)];

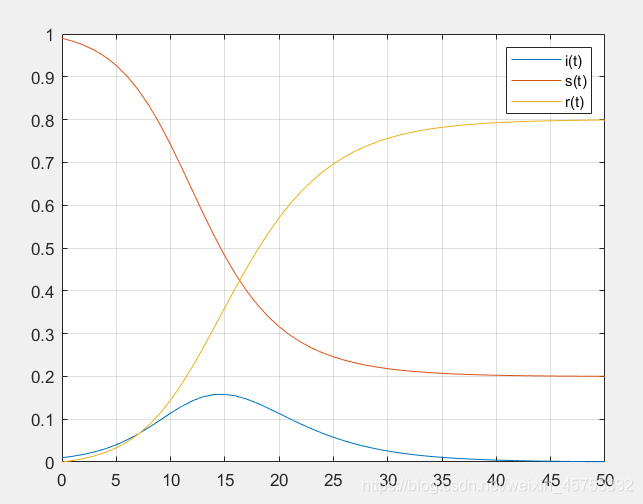
可以看出：s(t)单调减,r(t)单调增,都趋于稳定, i(t)先增后减趋于0.
结果分析
先回顾一下参数
$接触率 \lambda；治愈率 \mu ； 1/ \mu~平均传染期 (病人治愈所需平均时间)；\sigma =\lambda/\mu~接触数 (感染期内每个病人有效接触人数)$
可以分析出：

• 随着卫生健康思想水平高，接触率 $\lambda$变小
• 随着医疗水平的提高，治愈率 $\mu$增大
• 接触数 $\sigma =\lambda/\mu$减小——有助于控制传播.

我们可以试试稍微减少一下 $\lambda$，增大 $\mu$，来看下效果

ts=0:40;
x0=[0.01, 0.99];
[t,x]=ode45('ill',ts,x0);
r=1-x(:,1)-x(:,2);
plot(t,x(:,1),t,x(:,2),ts,r),grid
legend('i(t)','s(t)','r(t)')

function y=ill( t,x)
a=0.8;
b=0.6;
y=[a*x(1)*x(2)-b*x(1);-a*x(1)*x(2)];

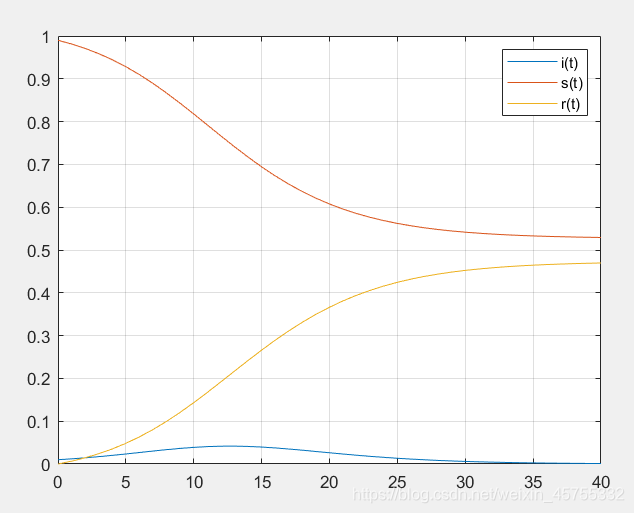
综上我们可以得出结论：想要减少传染病的传播，我们就要在接触数 $\sigma$上下功夫。

实战建模

数据处理

首先，我用python爬虫爬取了丁香医生官方数据，一共5534条数据 特征包括感染、死亡、治愈的总数，当日感染、死亡、治愈新增，疑似病例，时间，省份等14个特征

然后用python进行数据提取，提取了较为典型的湖北省的数据作为我的参考依据

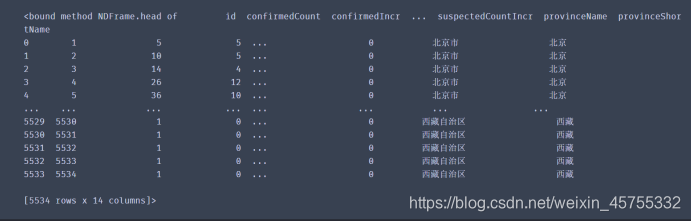
然后用python对数据进行清洗，提取出了患病总数，现存患者总数，死亡总数，治愈总数，时间，省份这几个特征

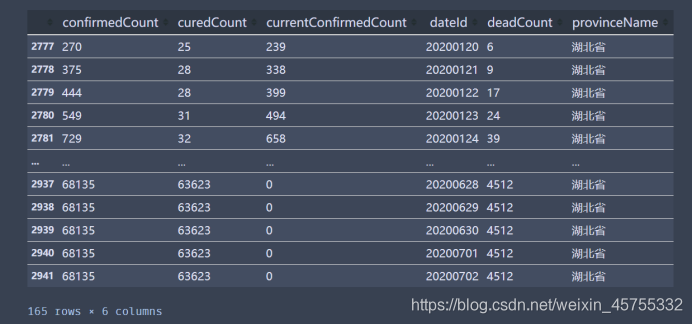
对日期格式进行修改，值保留月和日，并与死亡人数的位置交换

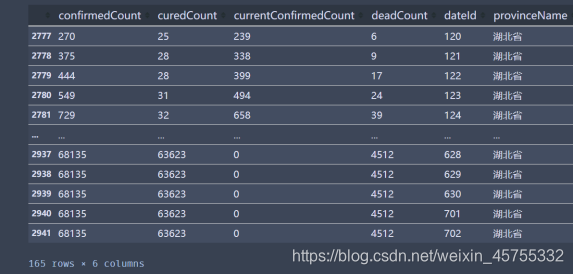
这里我用python对提取的四个特征分别进行了数据分析（主要包括计算最值，平均值等，），并把1.20日作为第一天，7.02日作为最后一天也就是第165天，做了可视化可视化处理。
感染人数示意图

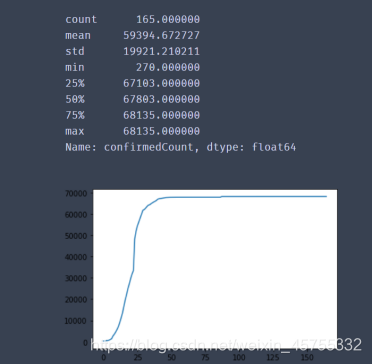
治愈人数示意图

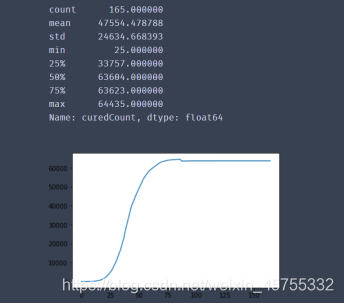
现存患者数量图

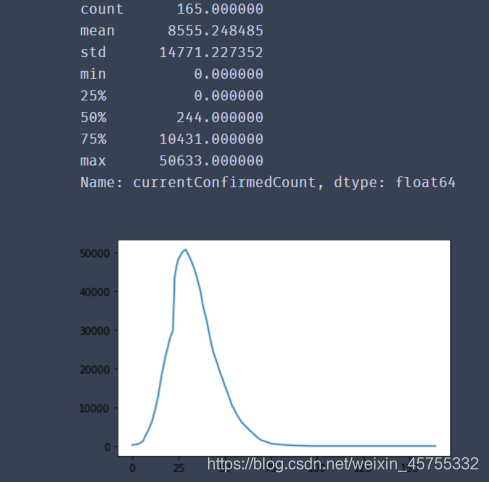
死亡人数示意图

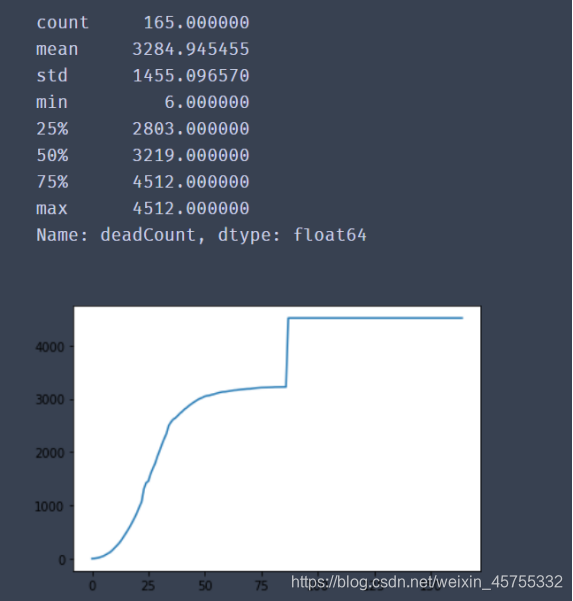
经过上面的图片与describe数据分析，我们发现有一天是异常的，患者多出了平时的十倍左右，经过查阅资料，这天因加强了检测标准，所以增多了很多。为了避免这个数据的影响我们选择将这一天删去（或者用平均数或中位数代替也可）
将上面清理过的数据存放到csv文件中

模型建立
模型假设
经过上面数据的分析，我们大体可以进行如下假设：
1.由于不存在封闭情况，考虑开放体系。
2.目前数据以天为单位发布，因此不考虑连续变化情况，只考虑离散的方程。
3.新型冠状病毒的治愈人数和死亡人数相对较 小，因此只考虑 Susceptible(易感)和 Infected(感染) 两类人群。设易感人群总数为N
4.经专家鉴定新冠病毒患者治愈后至少六个月之内不会再被感染，所以设治愈后移出易感人群。
5.设每个病人每天有效接触人数为 $\lambda$(日接触率)，且使接触的健康人致病.
6.设病人每天治愈的比例为 $\mu$(日治愈率)
7.时刻t健康人、病人和移出者的数量分别为 s(t), i(t), r(t).

模型一

分析可以得到移出者r(t)=治愈人数+死亡人数
通过python数据处理，我们算出了r(t)的值，并将其可视化

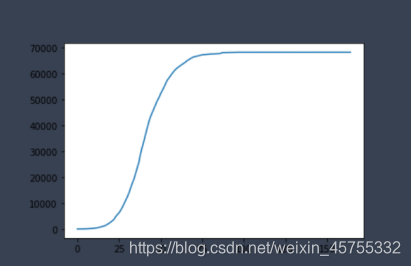
我用MATLAB对其进行了拟合，拟合图像为

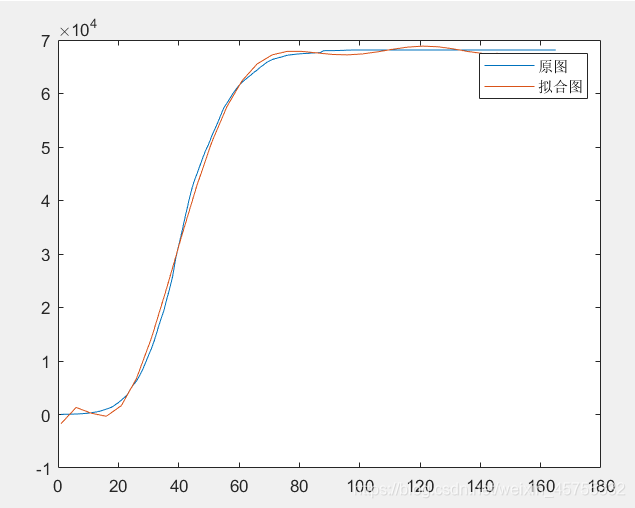
分析可以得到患者 i(t)=患病总数-移出者
可以通过csv文件的currentConfirmedCount 直接获得i(t)数据，当然也可以通过 i(t)=confirmedCountv - r(t)获得，对此我也做了可视化展示

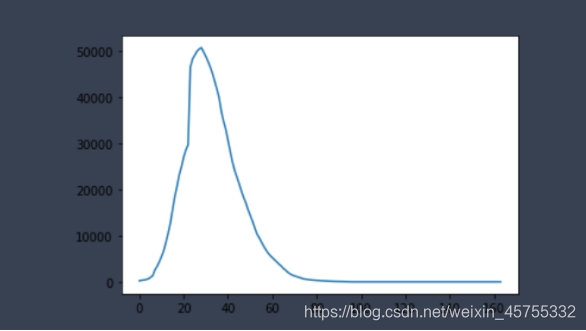
通过MATLAB程序对其进行拟合，可以得到r(t)的函数图像大致为

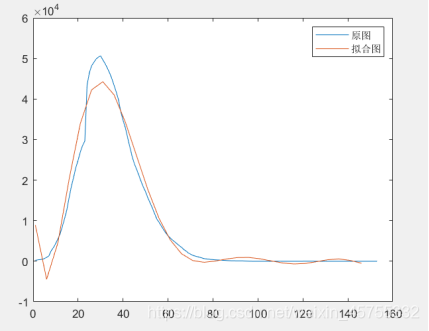
为了方便，利于公式推导，我们先设时刻t健康人、病人和移出者的数量分别为 s(t), i(t), r(t). 所以有

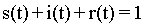
可以推导出每日新增病例的表达式

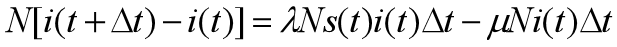
由以上两个公式可以推导出以下两个微分方程

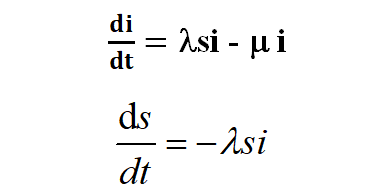
可以知道初值
$i(0)=i_0.s(0)=s_0$
因为一开始治愈的和死亡的肯定很少，所以r0可以看为0，于是就有：
$i_0+s_0=1$
通过解以上微分方程我们可以根据经验假设 $\lambda$ (日接触率)和 $\mu$(日治愈率)的值分别为1和0.5（也就是每个患者可能使1个正常人患病，患者可能有0.5的概率被治愈）；由于一开始患者肯定比正常人少很多，所以我们设i0=0.01,s0=0.99。对其求解可以得到s(t), i(t), r(t)，的变化图像

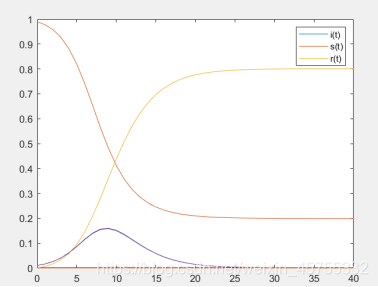
MATLAB程序如下
ts=0:40;
x0=[0.01, 0.99];
[t,x]=ode45(‘ill’,ts,x0);
r=1-x(:,1)-x(:,2);
plot(t,x(:,1),t,x(:,2),ts,r,ts,x(:,1)/x(:,2))
legend(‘i(t)’,‘s(t)’,‘r(t)’)

function y=ill( t,x)
a=1;
b=0.5;
y=[ax(1)x(2)-bx(1);-ax(1)*x(2)];

结果分析：患病人数肯定有个高潮，但之后高潮就会减弱，并逐步降低为0。随着医疗卫生条件的不断提升，患者的 $\lambda$(日接触率)肯定降低， $\mu$ (日治愈率)肯定上升，所以我们可以把 $\lambda$调一点为0.8， $\mu$调高一点为0.6，可以得到以下趋势图。所以应对传染病很关键的一点是我们要提高医疗卫生条件


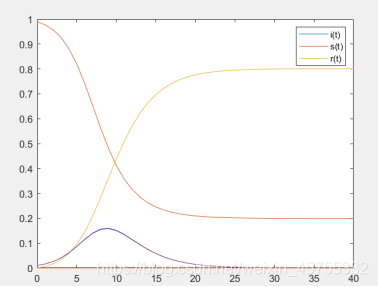
模型二

实际上， $\lambda$ (日接触率)和 $\mu$(日治愈率)都是随着时间变化的，这里我们设s(t), i(t), r(t) 为第t天健康人、病人、移除者(病愈与死亡之和)的数量， s(t)+ i(t)+r(t)=N.．
(t), (t) ~第t天感染率, 移除率(治愈率与死亡率之和)
有 $di/dt=\lambda (t)s(t)i(t) - (t)i(t)$
因为s远大于i, r，s(t)视为常数，所以有

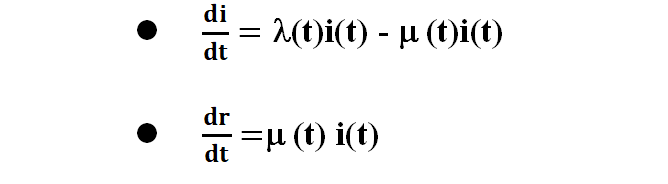
取差分近似导数

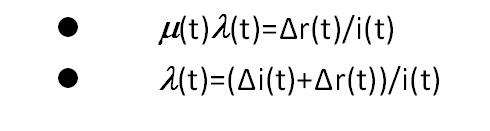
我们可以先用真实数据对(t)进行展示并进行拟合

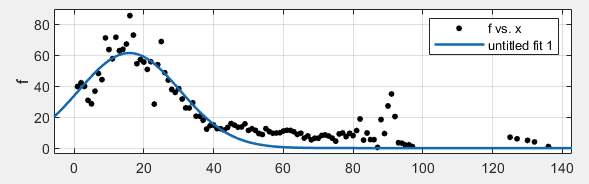
当然同样的方法对(t)进行拟合

做不出来了，好难，光这些东西就弄了四天，到了数学建模国赛得多难多累啊，哎，让我这个小白手足无措。毕竟还没有正规的培训，这个模型等期末考完试一定好好做做！！！
冲国奖
冲国奖
冲国奖