算法概论上机集合

实验一
实验目的与要求：理解分治法的基本思想和设计方法。
实验题目：
1．实现快速排序的算法,并尝试采用不同的方法实现线性的划分过程.
2. 有一个数的序列A[1]、A[2] 、A[3] 、…… 、A[n]，若i<j，并且A[i]>A[j]，则称A[i]与A[j]构成了一个逆序对，设计算法求数列A中逆序对的个数.
3. 引入逆序计数问题作为考察两个序列有多大差别的一个好的度量指标。但是人们可能感觉这个量度太敏感了。如果i<j，并且A[i]>2A[j]，我们把这对i,j叫做重要的逆序。设计一个O(nlogn) 的算法计数在两个序列中的重要逆序个数。
1

#include<iostream>
#include <vector>
#include"Sort.h"
#define MAXLENGTH 100
using namespace std;
int main(void)
{
	vector<int>A;
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		int temp;
		cin >> temp;
		A.push_back(temp);
	}
	QuickSort(A, 0, A.size() - 1);
	for (int i = 0; i < A.size(); i++)
	{
		cout << A[i] << " ";
	}
	cout << endl;
	int n2;
	int a[MAXLENGTH];
	cin >> n2;
	for (int i = 0; i < n2; i++)
	{
		cin >> a[i];
	}
	QuickSort_2(a, 0, n2 - 1);
	for(int i=0;i<n2;i++)
	{
		cout << a[i] << " ";
	}
	cout << endl;
	system("pause");
}

#include<iostream>
#define MAXLEN 100
using namespace std;
int merge(int A[], int begin, int mid, int end) 
{
	static int count = 0;
	int result[MAXLEN];
	int i = begin;
	int j = mid + 1;
	int k = 0;
	while (i <= mid && j <= end) 
	{
		if (A[i] <= A[j]) 
		{
			result[k++] = A[i++];
		}
		else 
		{
			count += mid - i + 1;
			result[k++] = A[j++];
		}
	}
	while (j <= end)
		result[k++] = A[j++];
	while (i <= mid)
		result[k++] = A[i++];
	for (k = 0; k < end - begin + 1; k++)
		A[begin + k] = result[k];
	return count;
}

int mergeSort(int a[], int begin, int end) {
	int sum = 0;
	if (begin < end) {
		int mid = (begin + end) / 2;
		mergeSort(a, begin, mid);
		mergeSort(a, mid + 1, end);
		sum = merge(a, begin, mid, end);
	}
	return sum;
}

int main(void) 
{
	int n;
	cin >> n;
	int a[MAXLEN];
	for (int i = 0; i < n; i++) 
	{
		int m;
		cin >> m;
		a[i] = m;
	}
	int begin = 0, end = n - 1;
	cout << mergeSort(a, begin, end);
	system("pause");
	return 0;
}

#include <iostream>
#define MAXLEN 100
using namespace std;
long long sum = 0;

void merge(int *s, int *temp, int left, int right, int mid)
{
	int i = left, j = mid + 1, k = left;
	int pointer = left;
	while (i <= mid && j <= right)
	{
		if (s[i] > s[j])
		{
			temp[k] = s[j];
			while (s[pointer] <= 2 * s[j] && pointer <= mid)
			{
				pointer++;
			}
			if (pointer != mid + 1)
			{
				sum += mid - pointer + 1;
			}
			j++;
		}
		else
		{
			temp[k] = s[i];
			i++;
		}
		k++;
	}

	while (i <= mid)
	{
		temp[k++] = s[i++];
	}
	while (j <= right)
	{
		temp[k++] = s[j++];
	}
	for (int i = left; i <= right; i++)
	{
		s[i] = temp[i];
	}
}

void mergeSort(int *s, int *temp, int left, int right)
{
	int mid = (left + right) / 2;
	if (left < right)
	{
		mergeSort(s, temp, left, mid);
		mergeSort(s, temp, mid + 1, right);
		merge(s, temp, left, right, mid);
	}
}


int s[MAXLEN] = {};
int temp[MAXLEN] = {};

int main() 
{
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> s[i];
	}
	mergeSort(s, temp, 0, n - 1);
	cout << sum << endl;
	system("pause");
	return 0;
}

实验二
实验目的与要求：理解分治法的基本思想和设计方法。

实验题目：

1．k-路合并操作问题
假定有k个有序数组，每个数组中含有n个元素，您的任务是将它们合并为单独的一个有序数组，该数组共有kn个元素。设计和实现一个有效的分治算法解决k-路合并操作问题，并分析时间复杂度。

查找中项问题
对于长度为n的整型数组A，随机生成其数组元素值，然后实现一个线性时间的算法，在该数组中查找其中项。
1

#include <iostream>
#include <vector>
using namespace std;
vector<int> mergeTowArrays(vector<int>A,vector<int>B)
{
	vector<int>temp;
	temp.resize(A.size() + B.size());
	int index = 0, j = 0, i = 0;
	while (i < A.size() && j < B.size())
	{
		if (A[i] < B[j])
			temp[index++] = A[i++];
		else
			temp[index++] = B[j++];
	}
		while (i < A.size())
			temp[index++] = A[i++];
		while (j < B.size())
			temp[index++] = B[j++];
		return temp;
}
vector<int> kMergeSort(vector<vector<int>>A, int start, int end)
{
	if (start >= end)
		return A[start];
	int mid = start + (end - start) / 2;
	vector<int>Left = kMergeSort(A, start, mid);
	vector<int>Right = kMergeSort(A, mid + 1, end);
	return mergeTowArrays(Left, Right);
}
vector<int> mergeSortArrays(vector <vector<int>>A)
{
	vector<int>temp;
	if (A.empty() || A.size() == 0 || A[0].size() == 0)
		return temp;
	temp = kMergeSort(A, 0, A.size() - 1);
	return temp;
}
int main(void)
{
	int k,n;
	cin >> k >> n;
	vector<vector<int>>A(k);
	for (int i = 0; i < k; i++)
	{
		A[i].resize(n);
	}
	for (int i = 0; i < A.size(); i++)
	{
		for (int j = 0; j < A[0].size(); j++)
			cin >> A[i][j];
	}
	vector<int>result;
	result = mergeSortArrays(A);
	for (int i = 0; i < result.size(); i++)
	{
		cout << result[i] << " ";
	}
	cout << endl;
	system("pause");
	return 0;
}

#include <iostream>
#include <vector>
using namespace std;
int select(vector<int>&A, int k,int n)
{
	int x = A[rand() % n];
	vector<int>small;
	small.resize(n);
	vector<int>big;
	big.resize(n);
	int equal,n_s=0,n_b=0;
	for (int i = 0; i < n; i++)
	{
		if (A[i] > x)
			big[n_b++] = A[i];
		else if (A[i] == x)
			equal = x;
		else
			small[n_s++] = A[i];
	}
	if (k <= n_s)
		return select(small, k,n_s);
	else if (k == n_s + 1)
		return equal;
	else
		return select(big, k - 1 - n_s,n_b);
}
int main(void)
{
	vector<int>A;
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		int temp;
		cin >> temp;
		A.push_back(temp);
	}
	int k = (1 + n) / 2;
	cout << select(A, k,n);
	system("pause");
	return 0;
}

实验三
实验目的与要求：理解分治法的基本思想和设计方法。

实验题目：

1．查找带权中位数
【问题描述】
给定一个未排序的数组(x1, x2, … ,xn)，其中每个元素关联一个权值：(w1, w2, … ,wn)，且。请设计一个线性时间的算法，在该数组中查找其带权中位数xk，满足：

2．寻找最邻近的点对
【问题描述】
设p1=(x1,y1), p2=(x2,y2), … , pn=(xn,yn) 是平面上n个点构成的集合S，设计和实现找出集合S中距离最近点对的算法。
1

扫描二维码关注公众号，回复： 11368302 查看本文章

#include <iostream>
#include <vector>
#include <iomanip>
using namespace std;
struct Node
{
	int value;
	double weight;
};
int partition(vector<Node>&A, int p, int r)
{
	int less = p - 1, i;
	int pivot = p + rand() % (r - p + 1);
	for (i = p; i <= r; i++)
	{
		if (A[i].value < A[pivot].value)
		{
			less++;
			swap(A[less], A[i]);
		}
	}
	swap(A[less + 1], A[pivot]);
	return less + 1;
}
int WeightedMedian(vector<Node>&A, int p, int r)
{
	if (p == r)
		return A[p].value;
	if (r - p == 1)
	{
		if (A[p].weight == A[r].weight)
			return (A[p].value + A[r].value) / 2;
		if (A[p].weight > A[r].weight)
			return A[p].value;
		else
			return A[r].value;
	}
	int q = partition(A, p, r);
	double wl = 0, wr = 0;
	for (int i = p; i <= q - 1; i++)
	{
		wl += A[i].weight;
	}
	for (int i = q + 1; i <= r; i++)
	{
		wr += A[i].weight;
	}
	if (wr < 0.5&&wl < 0.5)
		return A[q].value;
	else
	{
		if (wl > wr)
		{
			A[q].weight += wr;
			WeightedMedian(A, p, q);
		}
		else
		{
			A[q].weight += wl;
			WeightedMedian(A, q, r);
		}
	}
}
void Print(vector<Node>A)
{
	for (int i = 0; i < A.size(); i++)
		cout << A[i].value << " ";
	cout << endl;
	for (int i = 0; i < A.size(); i++)
		cout <</*setprecision(2)<< */A[i].weight<<" ";
	cout << endl;
}
void Initial(vector<int>&B,int n)
{
	for (int i = 0; i < n; i++)
	{
		B.push_back(0);
	}
}
int main(void)
{
	int n, sum = 0;
	cin >> n;
	vector<Node>A;
	vector<int>B;
	A.resize(n);
	B.resize(n);
	Initial(B,n);
	for (int i = 0; i < n; i++)
	{
		A[i].value = rand() % 100;
		do { B[i] = rand() % 100; } while (B[i] == 0);
		sum += B[i];
	}
	for (int i = 0; i < n; i++)
	{
		A[i].weight = (double)B[i] / sum;
	}
	Print(A);
	cout << WeightedMedian(A, 0, n - 1);
	system("pause");
	return 0;
}

/*设p1=(x1,y1), p2=(x2,y2), … , pn=(xn,yn) 是平面上n个点构成的集合S，设计和实现找出集合S中距离最近点对的算法。*/
/*10
4 3
1 4
2 3
2 6
3 9
4 6
7 5
8 9
10 6
9 3
*/
#include <iostream>
#include <algorithm>
#include <vector>
#include <math.h>
using namespace std;
struct Point 
{
	double x, y;
};
bool cmp_1(Point a, Point b) //sort排序参数
{
	return a.y < b.y;
}
bool cmp_2(Point a, Point b)
{
	return a.x < b.x;
}
double Dis(Point a, Point b)
{
	return sqrt((a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y));
}
double ClosestPoint(vector<Point>&A, int begin, int end, vector<Point>&rec)
{
	double d1=0, d2=0, d3=0, d=0;
	if (end - begin == 1) //一共仅两个点
	{
		rec[0].x = A[begin].x, rec[0].y = A[end].y;
		rec[1].x = A[begin].x, rec[1].y = A[end].y;
		return Dis(A[begin], A[end]);
	}
	if (end - begin == 2) //一共仅三个点
	{
		d1 = Dis(A[begin], A[begin + 1]);
		d2 = Dis(A[begin + 1], A[end]);
		d3 = Dis(A[begin], A[end]);
		if (d1 < d2&&d1 < d3)
		{
			rec[0].x = A[begin].x, rec[0].y = A[begin].y;
			rec[1].x = A[begin+1].x, rec[1].y = A[begin+1].y;
			return d1;
		}
		else if (d2 < d3)
		{
			rec[0].x = A[begin + 1].x, rec[0].y = A[begin + 1].y;
			rec[1].x = A[end].x, rec[1].y = A[end].y;
			return d2;
		}
		else
		{
			rec[0].x = A[begin].x, rec[0].y = A[begin].y;
			rec[1].x = A[end].x, rec[1].y = A[end].y;
			return d3;
		}
	}
	int mid = (begin + end) / 2; //递归开始
	vector<Point>temp_1, temp_2;//记录递归中的rec
	temp_1.resize(2);
	temp_2.resize(2);
	double left = ClosestPoint(A, begin, mid, rec);
	temp_1[0] = rec[0];
	temp_1[1] = rec[1];
	double right = ClosestPoint(A, mid + 1, end, rec);
	temp_2[0] = rec[0];
	temp_2[1] = rec[1];
	//d=min(left,right)
	if (left < right)
	{
		rec[0] = temp_1[0];
		rec[1] = temp_1[1];
		d = left;
	}
	else
	{
		d = right;
		rec[0] = temp_2[0];
		rec[1] = temp_2[1];
	}
	vector<Point> temp_3;
	for (int i = mid; i >= begin && (A[mid].x - A[i].x) < d; i--)
	{
		temp_3.push_back(A[i]);
	}
	for (int i = mid + 1; i <= end && (A[i].x - A[mid + 1].x) < d; i++)
	{
		temp_3.push_back(A[i]);
	}
	//对y进行排序
	sort(temp_3.begin(), temp_3.end(), cmp_1);
	for (int i = 0; i < temp_3.size(); i++)
	{
		for (int j = i + 1; j < temp_3.size(); j++)
		{
			if (temp_3[j].y - temp_3[i].y >= d)
				break;
			else
			{
				if (Dis(temp_3[i], temp_3[j]) < d)
				{
					rec[0].x = temp_3[i].x, rec[0].y = temp_3[i].y;
					rec[1].x = temp_3[j].x, rec[1].y = temp_3[j].y;
					d = Dis(temp_3[i], temp_3[j]);
				}
			}
		}
	}
	return d;
}
int main(void)
{
	vector<Point>p;
	int n;
	cin >> n;
	p.resize(n);
	for(int i=0;i<n;i++)
	{
		cin >> p[i].x >> p[i].y;
	}
	sort(p.begin(), p.end(), cmp_1);//对X排序
	vector<Point>rec;
	rec.resize(2);//记录最小距离的相邻两点
	double d_min = ClosestPoint(p, 0, n - 1, rec);
	cout << "最小距离的相邻两点为：(" << rec[0].x << "," << rec[0].y << "),(" << rec[1].x << "," << rec[1].y << ")" << endl;
	cout << "最小距离为：" << d_min << endl;
	system("pause");
	return 0;
}

实验四
实验目的与要求：掌握动态规划方法的基本思想与设计策略。

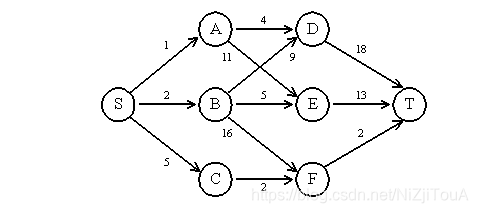
1．多段图中的最短路径问题
【问题描述】
建立一个从源点S到终点T的多段图，设计一个动态规划算法求出从S到T的最短路径值，并输出相应的最短路径。
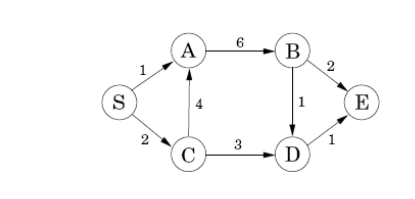
在这里插入图片描述
2．有向无环图中的最短路径问题
【问题描述】
建立一个从源点S到终点E的有向无环图，设计一个动态规划算法求出从S到E的最短路径值，并输出相应的最短路径。

最长递增子序列问题
【问题描述】
给定一个整数数组，设计一个动态规划算法求出该数组中的最长递增子序列。
1

/*建立一个从源点S到终点T的多段图，设计一个动态规划算法求出从S到T的最短路径值，并输出相应的最短路径。*
/*8 13
0 1 1
0 2 1
0 3 2
1 4 1
1 5 2
1 6 3
2 5 1
2 6 3
2 4 1
3 6 2
4 7 5
6 7 2
5 7 3
*/
#define MAX_ELEMENT 100000
#include<iostream>
#include <vector>
#include<queue>
using namespace std;
int main(void)
{
	int n, e;//顶点数和边数
	cin >> n >> e;
	vector<int>V;//顶点
	vector<vector<int>>edges;//边
	V.resize(n);
	edges.resize(n);
	for (int i = 0; i < n; i++)
	{
		edges[i].resize(n);
	}
	for (int i = 0; i < n; i++)
		V[i] = i;
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			if (i == j)
				edges[i][j] = 0;
			else
				edges[i][j] = MAX_ELEMENT;
		}
	}
	for (int i = 0; i < e; i++)
	{
		int va, vb, w;//两个顶点与权值
		cin >> va >> vb >> w;
		edges[va][vb] = w;
	}
	//BFS分段
	queue<int>nowqueue;
	queue<int>nextqueue;
	vector<vector<int>>subsection;
	vector<int>temp;
	bool *visited = new bool[n];
	int u;
	for (int i = 0; i < n; i++)
	{
		visited[i] = false;
	}
	for (int i = 0; i < n; i++)
	{
		if (!visited[i])
		{
			visited[i] = true;
			temp.push_back(i);
			subsection.push_back(temp);
			temp.clear();
			nowqueue.push(i);
			while (!nowqueue.empty())
			{
				u = nowqueue.front();
				nowqueue.pop();
				for (int j = 0; j < n; j++)
				{
					if (edges[u][j] != MAX_ELEMENT && edges[u][j] > 0 && !visited[j])
					{
						nextqueue.push(V[j]);
						temp.push_back(V[j]);
						visited[j] = true;
					}
				}
				if (nowqueue.empty()&&!temp.empty())
				{
					subsection.push_back(temp);
					nowqueue.swap(nextqueue);
					temp.clear();
				}
			}
		}
	}
	delete[]visited;
	//输出分段
	/*for (int i = 0; i < subsection.size(); i++)
	{
		cout << "第" << i+1 << "段" << ":";
		for (int j = 0; j < subsection[i].size(); j++)
			cout << subsection[i][j];
		cout << endl;
	}*/
	//寻找最短路径
	vector<int>nextPos;//距离尾节点最近的节点
	vector<int>dist;//节点到尾节点的距离
	nextPos.resize(n);
	dist.resize(n);
	//初始化
	dist[n - 1] = 0;
	nextPos[n - 1] = -1;
	for (int nowSub = subsection.size() - 2; nowSub >= 0; nowSub--)
	{
		for (int nowNodePos = 0; nowNodePos < subsection[nowSub].size(); nowNodePos++)
		{
			int nowpos = subsection[nowSub][nowNodePos];
			dist[nowpos] = MAX_ELEMENT;
			for (int lastSubNodeIndex = 0; lastSubNodeIndex < subsection[nowSub + 1].size(); lastSubNodeIndex++)
			{
				int lastSubNodePos = subsection[nowSub + 1][lastSubNodeIndex];
				if (edges[nowpos][lastSubNodePos] != MAX_ELEMENT && edges[nowpos][lastSubNodePos] > 0 && edges[nowpos][lastSubNodePos] + dist[lastSubNodePos]< dist[nowpos])
				{
					dist[nowpos] = edges[nowpos][lastSubNodePos] + dist[lastSubNodePos];
						nextPos[nowpos] = lastSubNodePos;
				}
			}
		}
	}
	cout << "最短路径:";
	cout << V[0];
	int tempIndex = V[0];
	while (tempIndex != V[n - 1])
	{
		cout << "-->" << nextPos[tempIndex];
		tempIndex = nextPos[tempIndex];
	}
	cout << endl;
	cout << "最短路径距离:" << dist[0] << endl;
	system("pause");
	return 0;
}

/*建立一个从源点S到终点E的有向无环图，设计一个动态规划算法求出从S到E的最短路径值，并输出相应的最短路径。
*/
#pragma once
#include <iostream>
#include <vector>
#include <deque>
#define NODE_COUNT 6
#define INF 255
using namespace std;

struct Node {
	int pos;
	int weight;
};

vector<Node> graph[NODE_COUNT];

int indegree[NODE_COUNT] = { 0 };
int beginPos;
int endPos;

void setEdge(vector<Node> graph[NODE_COUNT], int from, int to, int weight, int indegree[NODE_COUNT]) {
	//邻接表
	Node node;
	node.pos = to;
	node.weight = weight;
	graph[from].push_back(node);
	indegree[to]++;
}

void topoSort(vector<Node> graph[NODE_COUNT], int indegree[NODE_COUNT], vector<int>& linearList) {
	deque<int> queue;
	for (int i = 0; i < NODE_COUNT; i++) {
		if (indegree[i] == 0) {
			queue.push_back(i);
		}
	}
	while (!queue.empty()) {
		int pos = queue.front();
		queue.pop_front();
		linearList.push_back(pos);
		for (int j = 0; j < graph[pos].size(); j++) {
			if (!--indegree[graph[pos].at(j).pos]) {
				queue.push_back(graph[pos].at(j).pos);
			}
		}
	}
}

int getWeight(vector<Node> graph[NODE_COUNT], int from, int to) {
	for (int i = 0; i < graph[from].size(); i++) {
		if (graph[from][i].pos == to) {
			return graph[from][i].weight;
		}
	}
	return INF;

}

void findMinRoute(vector<Node> graph[NODE_COUNT], int beginPos, int endPos, vector<int> linearlist) {
	int nextPos[NODE_COUNT];
	int dist[NODE_COUNT];
	for (int i = 0; i < NODE_COUNT; i++) {
		dist[i] = getWeight(graph, i, endPos);
	}
	dist[endPos] = 0;
	for (int i = NODE_COUNT - 2; i >= 0; i--) {
		int nowpos = linearlist[i];
		for (int j = 0; j < graph[nowpos].size(); j++) {
			if (graph[nowpos][j].weight + dist[graph[nowpos][j].pos] <= dist[nowpos]) {
				nextPos[nowpos] = graph[nowpos][j].pos;
				dist[nowpos] = graph[nowpos][j].weight + dist[graph[nowpos][j].pos];

			}
		}
	}
	cout << "最短路径长为:" << dist[beginPos] << endl;
	cout << "最短路径为:";
	int temp = beginPos;
	cout << beginPos;
	while (temp != endPos) {
		cout << "-->" << nextPos[temp];
		temp = nextPos[temp];
	}
	cout << "\n";
}

int main(void) {

	beginPos = 0;
	endPos = 5;

	setEdge(graph, 0, 1, 1, indegree);
	setEdge(graph, 0, 2, 2, indegree);
	setEdge(graph, 1, 3, 6, indegree);
	setEdge(graph, 2, 1, 4, indegree);
	setEdge(graph, 2, 4, 3, indegree);
	setEdge(graph, 3, 4, 1, indegree);
	setEdge(graph, 3, 5, 2, indegree);
	setEdge(graph, 4, 5, 1, indegree);

	vector<int> list;
	topoSort(graph, indegree, list);
	cout << "拓扑排序:";
	for (int i = 0; i < list.size(); i++) {
		cout << list[i] << " ";
	}
	cout << "\n";

	findMinRoute(graph, beginPos, endPos, list);
	system("pause");
	return 0;
}

/*给定一个整数数组，设计一个动态规划算法求出该数组中的最长递增子序列。*/
/*input :一个数字序列，以空格分隔，以.结束
output:最长递增子序列*/
#include <iostream>
#include <vector>
using namespace std;
// 最长递增序列 <动态规划> <复杂度0(NlogN)>
vector<int> getdp2(vector<int> &arr);
vector<int> generateLIS(vector<int> &arr, vector<int>&dp);
int max(int i, int j) {
	if (i > j) return i;
	else return j;
}

int main() {
	vector<int> arr;
	int temp;
	while (cin >> temp) {
		arr.push_back(temp);
	}
	vector<int> dp = getdp2(arr);
	vector<int> lis = generateLIS(arr, dp);
	cout << "最长递增子序列为：";
	for (int i = 0; i < lis.size(); i++) {
		cout << lis[i] << " ";
	}
	cout << endl;
	cout << "长度为：" << lis.size() << endl;
	system("pause");
	return 0;
}


vector<int> getdp2(vector<int> &arr) {
	vector<int> dp(arr.size(), 0);
	vector<int> ends(arr.size(), 0);
	ends[0] = arr[0]; dp[0] = 1;
	int right = 0; int l = 0; int r = 0; int m = 0;
	for (int i = 1; i < arr.size(); i++) {
		l = 0;
		r = right;
		while (l <= r) 
		{ 
			m = (l + r) / 2;
			if (arr[i] > ends[m]) {
				l = m + 1;
			}
			else {
				r = m - 1;
			}
		}
		right = max(right, l);
		ends[l] = arr[i];
		dp[i] = l + 1;
	}
	return dp;
}


vector<int> generateLIS(vector<int> &arr, vector<int> &dp) {
	int len = 0; int index = 0;
	for (int i = 0; i < dp.size(); i++) { //寻最长递增子序列末尾的位置和值
		if (dp[i] > len) {
			len = dp[i];
			index = i;
		}
	}
	vector<int> lis(len, 0);
	lis[--len] = arr[index];
	for (int i = index; i >= 0; i--) {
		if (arr[i] < arr[index] && dp[i] == dp[index] - 1) {
			lis[--len] = arr[i];
			index = i;
		}
	}
	return lis;
}

实验五
实验目的与要求：掌握动态规划方法的基本思想与设计策略。

1．矩阵连乘问题
【问题描述】
给定n个矩阵{A1，A2，…,An},其中AiAi+1是可乘的，i=1，2，…，n-1,考察这n个矩阵的连乘积A1A2…An，设计一个动态规划算法，求出这个矩阵连乘积问题的最优计算顺序。
实现要求：随机生成n个合法的可连乘的矩阵，以完全加括号的方式输出其最优计算顺序。

2．最长公共子序列问题
【问题描述】
⑴ 给定两个字符串X和Y，设计一个动态规划算法，求出这两个字符串的最长公共子序列，并输出该子序列。

⑵ 若仅要求求出两个字符串的最长公共子序列的长度值，为节省存储空间，采用“滚动数组”方式实现动态规划算法。
1

/*给定n个矩阵{A1，A2，…,An},其中AiAi+1是可乘的，i=1，2，…，n-1,考察这n个矩阵的连乘积A1A2…An，设计一个动态规划算法，求出这个矩阵连乘积问题的最优计算顺序。
实现要求：随机生成n个合法的可连乘的矩阵，以完全加括号的方式输出其最优计算顺序。*/
#include<iostream>
#include <vector>
#define PNUM 100
using namespace std;
int p[PNUM];//矩阵维度
int m[PNUM][PNUM];//最优解
int c[PNUM][PNUM];//断开位置
void mul_Matrix(int n)
{
	for (int i = 1; i <= n; i++)
		m[i][i] = 0;
	for (int matrix_num = 2; matrix_num <= n; matrix_num++)//矩阵个数
	{
		for (int begin = 1; begin <= n - matrix_num + 1; begin++)//起始位置
		{
			int end = begin + matrix_num - 1;//结尾
			m[begin][end] = m[begin + 1][end] + p[begin - 1] * p[begin] * p[end];//从begin处断开，求最优断开位置
			c[begin][end] = begin;//记录当前断开位置
			for (int k = begin + 1; k < end; k++)//寻找最优断开位置
			{
				int q = m[begin][begin + 1] + m[begin + 1][end] + p[begin - 1] * p[begin] * p[begin + 1];
				if (q < m[begin][end])
				{
					m[begin][end] = q;
					c[begin][end] = k;
				}
			}
		}
	}
}
void traceBack(int begin, int end)
{
	if (begin == end) //basecase
		cout << "A" << begin;
	else
	{
		cout << "(";
		traceBack(begin, c[begin][end]);
		traceBack(c[begin][end]+1, end);
		cout << ")";
	}
}
int main()
{
	int n;
	cin >> n;//矩阵个数
	int end;
	//产生1-15之间的随机维数矩阵
	for (int i = 0; i <= n; i++)
	{
		p[i] = rand() % 15 + 1;
	}
	for (int i = 0; i < n; i++)
	{
		cout <<"A"<<i+1<<":"<< p[i] << "*" << p[i + 1] << endl;
	}
	mul_Matrix(n);
	cout << m[1][n] << endl;//最少相乘次数
	traceBack(1, n);
	system("pause");
	return 0;
}

/*⑴ 给定两个字符串X和Y，设计一个动态规划算法，求出这两个字符串的最长公共子序列，并输出该子序列。*/
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100;
char a[N], b[N];
int dp[N][N];
int flag[N][N];
void Print_LSC(int i, int j)
{
	if (i == 0 || j == 0)///递归终止条件
	{
		return;
	}
	if (!flag[i][j])
	{
		Print_LSC(i - 1, j - 1);
		cout << a[i - 1];
	}
	else if (flag[i][j] == 1)
	{
		Print_LSC(i - 1, j);
	}
	else if (flag[i][j] = -1)
	{
		Print_LSC(i, j - 1);
	}
}
int main()
{
	int lena, lenb, i, j;
	cin >> lena >> lenb;
	for (int i = 0; i < lena; i++)
		cin >> a[i];
	for (int i = 0; i < lenb; i++)
		cin >> b[i];
	//初始化
	memset(dp, 0, sizeof(dp));
	memset(flag, 0, sizeof(flag));
	for (i = 1; i <= lena; i++)
		{
		for (j = 1; j <= lenb; j++)
		{
			if (a[i - 1] == b[j - 1])
			{
				dp[i][j] = dp[i - 1][j - 1] + 1;
				flag[i][j] = 0;///来自于左上方
			}
			else
				{
				if (dp[i - 1][j] > dp[i][j - 1])
				{
					dp[i][j] = dp[i - 1][j];
					flag[i][j] = 1;///来自于左方
				}
				else
				{
					dp[i][j] = dp[i][j - 1];
					flag[i][j] = -1;///来自于上方
				}
			}
		}
	}
	Print_LSC(lena, lenb);
	system("pause");
	return 0;
}

/*若仅要求求出两个字符串的最长公共子序列的长度值，为节省存储空间，采用“滚动数组”方式实现动态规划算法。*/
#include <iostream>
#include<algorithm>
#define MAXNUM 100
using namespace std;
char a[MAXNUM], b[MAXNUM];
int dp[MAXNUM];//第i行
int pre[MAXNUM];//第i-1行

int main()
{
	int lena, lenb, j,i;
	cin >> lena >> lenb;
	//初始化
	for (int i = 0; i < lena; i++)
		cin >> a[i];
	for (int i = 0; i < lenb; i++)
		cin >> b[i];
	memset(dp, 0, sizeof(dp));
	memset(pre, 0, sizeof(pre));
	for (i = 1; i <= lena; i++) {
		for (j = 1; j <= lenb; j++)
		{
			if (a[i - 1] == b[j - 1])
				dp[j] = pre[j - 1] + 1;
			else
				dp[j] = max(dp[j - 1], pre[j]);
			pre[j - 1] = dp[j - 1];                    
		}
		pre[lenb] = dp[lenb];         //最后一个字符
	}
	cout << pre[lenb];
	system("pause");
	return 0;
}

实验六
实验目的与要求：掌握动态规划方法的基本思想与设计策略。

1．0-1背包问题
【问题描述】
给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为W（假定物品重量与背包容量值均为整数），应如何选择装入背包中的物品，使得装入背包中物品的总价值最大？设计一个动态规划算法，求解背包问题。

2.树中的最大独立集问题
【问题描述】
给定一个无回路的无向图（即树），设计一个动态规划算法，求出该图的最大独立集，并输出该集合中的各个顶点值。
1

/*给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为W（假定物品重量与背包容量值均为整数）
，应如何选择装入背包中的物品，使得装入背包中物品的总价值最大？设计一个动态规划算法，求解背包问题。*/
#include <iostream>
#include <vector>
using namespace std;
void knapsack(int products_count, int capacity, vector<int>&weight, vector<int>&value,vector<vector<int>>&result)
{
	for (int i = 1; i <= products_count; i++)
	{
		for (int w = 1; w <= capacity; w++)
		{
			if (weight[i] <= w)
			{
				if (value[i] + result[i - 1][w - weight[i]] > result[i - 1][w])
				
					result[i][w] = value[i] + result[i - 1][w - weight[i]];
				
				else
					result[i][w] = result[i - 1][w];
			}
			else
				result[i][w] = result[i - 1][w];
		}
	}
}
void Print(vector<vector<int>>&result, vector<int>weight, vector<int>&x, int products_count, int capacity)
{
	for (int i = products_count; i >= 2; i--)
	{
		if (result[i][capacity] == result[i - 1][capacity])
			x[i] = 0;
		else
		{
			x[i] = 1;
			capacity = capacity - weight[i];
		}
	}
	x[1] = result[1][capacity] ? 1 : 0;
}
int main()
{
	int products_count, capacity;
	vector<int>weight(1, 0);
	vector<int>value(1, 0);
	//输入商品个数和背包容量
	cin >> products_count >> capacity;
	//输入商品重量与价格
	for (int i = 1; i <= products_count; i++)
	{
		int temp;
		cin >> temp;
		weight.push_back(temp);
	}
	for (int i = 1; i <= products_count; i++)
	{
		int temp;
		cin >> temp;
		value.push_back(temp);
	}
	vector<vector<int>>result(products_count + 1, vector<int>(capacity + 1, 0));//初始化结果矩阵
	knapsack(products_count, capacity, weight, value, result);
	vector<int>x(6, 0);
	Print(result, weight, x, products_count, capacity);
	for (int i = 1; i <= products_count; i++)
		cout << x[i] << " ";
	cout << endl;
	cout << result[products_count][capacity] << endl;
	system("pause");
	return 0;
}

/*给定一个无回路的无向图（即树），设计一个动态规划算法，求出该图的最大独立集，并输出该集合中的各个顶点值。*/
#include <iostream>
#include <vector>
#include <cstdio>
#include <cstring>

using namespace std;

#define maxn 100
vector<int> v[maxn];
int d[maxn], s[maxn], gs[maxn];
int max(int i, int j)
{
	if (i > j) return i;
	else return j;
}
int dfs(int n, int fa)
{
	for (int i = 0; i < v[n].size(); i++)
	{
		int m = v[n][i];
		if (m != fa)
			dfs(m, n);
		s[n] += d[m];
		if (fa != -1)
			gs[fa] += d[m];
	}
	d[n] = max(s[n], gs[n] + 1);
	return d[n];
}
int main()
{
	int n;
	while (cin >> n)
	{
		for (int i = 0; i < n; i++)
			v[i].clear();
		for (int i = 0; i < n - 1; i++)
		{
			int a, b;
			cin >> a >> b;;
			v[a].push_back(b);
			v[b].push_back(a);
		}
		memset(d, 0, sizeof(d));
		memset(s, 0, sizeof(s));
		memset(gs, 0, sizeof(gs));
		cout << dfs(1, -1) << endl;
	}
	system("pause");
	return 0;
}

实验七
实验目的与要求：
（1）掌握贪心法的基本思想和设计方法。

1．区间调度问题
【问题描述】
给定n个活动，其中的每个活动ai包含一个起始时间si与结束时间fi。设计与实现算法从n个活动中找出一个最大的相互兼容的活动子集S。

要求：分别设计动态规划与贪心算法求解该问题。其中，对贪心算法分别给出递归与迭代两个版本的实现。

/*给定n个活动，其中的每个活动ai包含一个起始时间si与结束时间fi。设计与实现算法从n个活动中找出一个最大的相互兼容的活动子集S。

要求：分别设计动态规划与贪心算法求解该问题。其中，对贪心算法分别给出递归与迭代两个版本的实现。*/
#include <iostream>
#include <vector>
using namespace std;
vector<int>Start{0,1,3,0,5,3,5,6,8,8,2,12,1000};
vector<int>End{0,4,5,6,7,8,9,10,11,12,13,14,1000 };
void recursive(vector<int> S, vector<int> E, int i, int j)
{
	int m = i + 1;
	while (m <= j&&S[m] < E[i])
		m = m + 1;
	if (m <= j)
	{
		cout << m << " ";
		recursive(S, E, m, j);
	}
}
void iterative(vector<int>S, vector<int>E)
{	
	vector<int>A = { 1 };
	int i = 1;
	for (int m = 2; m < S.size()-1; m++)
	{
		if (S[m] > E[i])
		{
			A.push_back(m);
			i = m;
		}
	}
	for (int i = 0; i < A.size(); i++)
		cout << A[i] << " ";
}
int Dp(vector<int>S, vector<int>E)
{
	int n = S.size();
	int **C = new int*[n];
	for (int i = 0; i < n; i++)
		C[i] = new int[n];
	for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
			C[i][j] = 0;
	for(int j=0;j<n;j++)
		for (int i = 0; i < n; i++)
		{
			if (i < j)
			{
				for(int k=i+1;k<j;k++)
					if (S[k] >= E[i] && E[k] <= S[j])
					{
						if (C[i][j] < C[i][j] + C[k][j] + 1)
							C[i][j] = C[i][j] + C[k][j] + 1;
					}
			}
		}
/*	for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
		{
			cout << C[i][j] << " ";
			if (j == n - 1)
				cout << endl;
		}*/
	return C[0][n - 1];
}
int main()
{
	recursive(Start, End, 0, 11);
	cout << endl;
	iterative(Start, End);
	cout << endl;
	cout<<Dp(Start, End);
	system("pause");
	return 0;
}

实验八

实验目的与要求：
（1）掌握贪心法的基本思想和设计方法。

1．区间划分问题
【问题描述】
给定一组报告，其中的每个报告设置了一个开始时间si和结束时间fi。设计与实现一个算法，对这组报告分配最少数量的教室，使得这些报告能无冲突的举行。

2．最小延迟调度问题
【问题描述】
假定有一单个的资源在一个时刻只能处理一个任务。现给定一组任务，其中的每个任务i包含一个持续时间ti和截止时间di。设计与实现一个算法，对这组任务给出一个最优调度方案，使其对所有任务的最大延迟最小化。
1

/*给定一组报告，其中的每个报告设置了一个开始时间si和结束时间fi。设计与实现一个算法，对这组报告分配最少数量的教室，使得这些报告能无冲突的举行。*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;

#define MAXNUM 5000
struct Report {
	int startTime;
	int endTime;
	int id;
	friend bool operator <(Report a, Report b) {
		return a.endTime > b.endTime;
	}//小顶堆
};
bool cmp(Report a, Report b) {
	return a.startTime < b.startTime;
}
void selectRoom(Report rep[], int classRoom[], int n) {
	sort(rep, rep + n, cmp);
	priority_queue<Report>que;
	int classRoomNum = 0;
	que.push(rep[0]);
	classRoom[rep[0].id] = ++classRoomNum;
	for (int i = 1; i < n; i++)
	{
		Report temp = que.top();
		if (temp.endTime < rep[i].startTime)
		{
			classRoom[rep[i].id] = classRoom[temp.id];
			que.pop();
			que.push(rep[i]);
		}
		else
		{
			classRoom[rep[i].id] = ++classRoomNum;
			que.push(rep[i]);
		}
	}
	cout <<"教室个数:" <<classRoomNum << endl;
}
int main(void)
{
	Report rep[MAXNUM];
	int classRoom[MAXNUM];
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> rep[i].startTime >> rep[i].endTime;
		rep[i].id = i;
	}
	selectRoom(rep, classRoom, n);
	for (int i = 0; i < n; i++)
	{
		cout << classRoom[i]<<" ";
	}
	system("pause");
	return 0;
}

/* 假定有一单个的资源在一个时刻只能处理一个任务。现给定一组任务，其中的每个任务i包含一个持续时间ti和截止时间di。
设计与实现一个算法，对这组任务给出一个最优调度方案，使其对所有任务的最大延迟最小化。
*/
#include<iostream>
#include <algorithm>
#define MAXNUM 100
using namespace std;

struct Mission {
	int id;
	int lastTime;
	int endTime;
};
bool cmp(Mission a, Mission b)
{
	return a.endTime <= b.endTime;
}
void select_Mission(Mission mi[], int n)
{
	sort(mi, mi + n, cmp);
	int delay = 0;
	int startTime[MAXNUM + 1];
	startTime[1] = 0;
	if (startTime[1] + mi[0].lastTime > mi[0].endTime)
		delay += startTime[1] + mi[0].lastTime - mi[0].endTime;
	for (int i = 1; i < n; i++)
	{
		startTime[i + 1] = startTime[i] + mi[i - 1].lastTime;
		if (startTime[i + 1] + mi[i].lastTime > mi[i].endTime)
			delay += startTime[i + 1] + mi[i].lastTime - mi[i].endTime;
	}
	cout << "最小延迟" << delay << endl;
	for (int i = 0; i < n; i++)
		cout << "任务:" << mi[i].id << "执行时间区间：（" << startTime[i + 1] << "," << mi[i].lastTime + startTime[i + 1] << ")" << endl;
}
int main()
{
	Mission mi[MAXNUM];
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		mi[i].id = i + 1;
		cin >> mi[i].lastTime >> mi[i].endTime;
	}
	select_Mission(mi, n);
	system("pause");
	return 0;
}

实验九
实验目的与要求：
（1）掌握使用图的深度优先搜索算法实现对有向图中是否包含环的判断；
（2）掌握使用图的深度优先搜索算法实现对有向图的强连通分量的划分。

1．有向图中环的判断问题
【问题描述】
给定一个有向图，要求使用深度优先搜索策略，判断图中是否存在环。

2．有向图的强连通分量问题
【问题描述】
给定一个有向图，设计一个算法，求解并输出该图的各个强连通分量。
1

/*给定一个有向图，要求使用深度优先搜索策略，判断图中是否存在环。*/
#include <iostream>
#include <vector>
#define MAXNUM 1000

using namespace std;
vector<int> AList[MAXNUM];
int color[MAXNUM];//-1==white,0==gray,1==black
bool is_ADG;
void dfs(int x)
{
	if (is_ADG)
		return;
	color[x] = 0;
	for (int i = 0; i < AList[x].size(); i++)
	{
		if (color[AList[x][i]] == -1)
			dfs(AList[x][i]);//未被访问，继续搜索
		else if (color[AList[x][i]] == 0)
		{
			is_ADG = true;
			return;
		}//gray—>gray，回边，存在环
	}
	color[x] = 1;//访问结束，black
}

int main(void)
{
	memset(color, -1, sizeof(color));//初始化=white
	int vexNnm, edgeNum;
	cin >> vexNnm >> edgeNum;
	for (int i = 0; i < edgeNum; i++)
	{
		int u, v;
		cin >> u >> v;//u—>v
		AList[u].push_back(v);
	}
	is_ADG = false;
	dfs(1);
	if (is_ADG)
		cout << "有向图存在环" << endl;
	else
		cout << "有向图无环" << endl;	
	system("pause");
	return 0;
}

/*给定一个有向图，设计一个算法，求解并输出该图的各个强连通分量。*/
#include <iostream>
#include <list>
#include <stack>
using namespace std;
class Graph {
private:
	int vexNum;//顶点数
	list<int> *adj;//领接表
	void vexOrder(int v, bool visited[], stack<int>&Stack) //根据DFS访问结束时间对各个顶点入栈
	{
		visited[v] = true;
		for (list<int>::iterator i = adj[v].begin(); i != adj[v].end(); i++) {
			if (!visited[*i])
				vexOrder(*i, visited, Stack);
		}
		Stack.push(v);//从v出发可到达的所有顶点已访问，v入栈。
	}
	void DFS(int v, bool visited[]) {
		visited[v] = true;
		cout << v << " ";
		for (list<int>::iterator i= adj[v].begin(); i != adj[v].end(); i++) {
			if (!visited[*i])
				DFS(*i, visited);
		}
	}
public:
	Graph(int vexNum) {
		this->vexNum = vexNum;
		adj = new list<int>[vexNum];
	}
	Graph ReverseGraph() {
		Graph g(vexNum);
		for (int i = 0; i < vexNum; i++)
		{
			for (list<int>::iterator j = adj[i].begin(); j != adj[i].end(); j++)
			{	
				g.adj[*j].push_back(i);
			}
		}
		return g;
	}
	void addEdge(int v, int w)
	{
		adj[v].push_back(w);
	}
	void printSCC() {
		stack<int> Stack;
		bool *visited = new bool[vexNum];
		for (int i = 0; i < vexNum; i++)
			visited[i] = false;
		for (int i = 0; i < vexNum; i++)
			if(visited[i]==false)
				vexOrder(i, visited, Stack);
		Graph Gr = ReverseGraph();
		for (int i = 0; i < vexNum; i++)
			visited[i] = false;
		while (!Stack.empty())
		{
			int v = Stack.top();
			Stack.pop();
			if (visited[v] == false)
			{
				Gr.DFS(v, visited);
				cout << endl;
			}
		}
	}
};
int main(void)
{
	Graph g(5);
	g.addEdge(1, 0);
	g.addEdge(0, 2);
	g.addEdge(2, 1);
	g.addEdge(0, 3);
	g.addEdge(3, 4);
	g.printSCC();
	system("pause");
	return 0;
}

实验十
实验目的与要求：
（1）掌握使用图的深度优先搜索算法实现对无向图双连通分量的划分算法；
（2）理解与掌握在含负权值边的图中求最短路径问题的算法。

1．无向图的双连通分量划分问题
【问题描述】
给定一个无向图，设计一个算法，判断该图中是否存在关节点，并划分双连通分量。

带负权值边的有向图中的最短路径路径问题
【问题描述】
对于一个带负权值边的有向图，实现Bellman-Ford算法，求出从指定顶点s到其余顶点的最短路径，并判断图中是否存在负环。
1

package 带负权值的有向图中的最短路径;

public class MGraph {
	private int [][] edges;
	private int vexNum;
	private int []dist;//源点到该顶点的距离
	private int maxDistant;//无穷大
	
	public MGraph(int [][]edges){
		this.edges=edges;
		this.vexNum=edges.length;
		this.dist=new int[vexNum];
		this.maxDistant=100000;//∞
	}
	public boolean bellmanFord(int begin) {
		for(int i=0;i<vexNum;i++)
			dist[i]=maxDistant;
		dist[begin]=0;
		for(int i=0;i<vexNum-1;i++) {//遍历从源点出发到任一顶点的n-1条边
			boolean flag=false; //是否存在更短路径
			for(int j=0;j<vexNum;j++) {
				for(int k=0;k<vexNum;k++) {
					if(edges[j][k]!=0&&dist[k]>dist[j]+edges[j][k]) {
						dist[k]=dist[j]+edges[j][k];
						flag=true;
					}
				}
			}
			if(flag==false)
				break;
		}
		//从源点到某个顶点有n条边且路径更短，则存在环
		for(int i=0;i<vexNum;i++)
			for(int j=0;j<vexNum;j++)
				if(edges[i][j]!=0&&dist[j]>dist[i]+edges[i][j])
					return false;
		for(int i=0;i<vexNum;i++)
			System.out.println(i+":"+dist[i]);
		return true;
	}
}
package 带负权值的有向图中的最短路径;
/*对于一个带负权值边的有向图，实现Bellman-Ford算法，
 * 求出从指定顶点s到其余顶点的最短路径，
 * 并判断图中是否存在负环。*/
public class NEDGraph {
	 public static void main(String[] args) {
	        // TODO Auto-generated method stub
	        int[][] edges=new int[][]{
	            {0,10,0,4,1},
	            {0,0,0,0,0},
	            {0,-10,0,0,0},
	            {0,0,0,0,0},
	            {0,0,2,0,0}
	        };
	        MGraph m1=new MGraph(edges);
	        System.out.println(m1.bellmanFord(0));
	    }
}

package UGraphBiC;

public class Edge {
	private int u;
	private int v;
	
	public Edge(int u,int v)
	{
		this.u=u;
		this.v=v;
	}

	public int getU() {
		return u;
	}

	public void setU(int u) {
		this.u = u;
	}

	public int getV() {
		return v;
	}

	public void setV(int v) {
		this.v = v;
	}
}
package UGraphBiC;
import java.util.Stack;
public class MGraph{
	private int vexNum;
	private int [][]edges;
	private Stack<Edge>edgeStack;
	private int [] color;//-1为白色 0为灰色 1为黑色
	private int [] pre;
	private int [] post;
	private int clock;
	

	public MGraph(int[][] edges) {
		super();
		this.vexNum = edges.length;
		this.edges = edges;
		this.edgeStack = new Stack<>();
		this.color = new int[vexNum];
		this.pre = new int[vexNum];
		this.post = new int[vexNum];
		this.clock = 1;
		for(int i=0;i<vexNum;i++)
			color[i]=-1;
	}
	public int biDFS(int v) {
		color[v]=0;
		pre[v]=clock;
		clock++;
		
		int back=pre[v];    //表示从v出发，经过一条其后代组成的边包括回退边,所能访问到的顶点的最小的开始搜索时间
        
        for(int i=0;i<vexNum;i++){
            if(edges[v][i]==1 && color[i]!=1){
                
                edgeStack.push(new Edge(v,i));    
                
                if(color[i]==-1){                 //树边
                    int wBack=biDFS(i);
                    
                    if(wBack>=pre[v]){          //说明v的子树没有回路关联到v的祖先
                        System.out.println("双连通部件: ");
                        Edge e=edgeStack.pop();
                        while(true){
                            System.out.println("("+e.getU()+","+e.getV()+") ");
                            if(e.getU()==v && e.getV()==i)
                                break;
                            e=edgeStack.pop();
                        }
                    }
                    if(wBack<back)
                        back=wBack;
                }else if(color[i]==0){            //回边
                    if(pre[i]<back)
                        back=pre[i];
                }
            }
        }
       
        post[v]=clock;
        clock++;
        color[v]=1;
        return back;
    }
}
package UGraphBiC;
import java.util.Stack;
public class UGraphBiC {
	public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[][] graph=new int[][]{
            {0,1,1,0,0},
            {1,0,1,0,0},
            {1,1,0,1,1},
            {0,0,1,0,1},
            {0,0,1,1,0}
        };
        MGraph m=new MGraph(graph);
        m.biDFS(0);
    }
}

实验十二（十一）
实验目的与要求：
（1）学会应用最大流与最小割算法解决实际问题。

设计与实现二部图最大匹配（Bipartite Matching）问题的求解算法。
设计与实现项目选择（Project Selection）问题的算法。
设计与实现调查设计（Survey Design）问题的算法。
1
二部图：

/*
设计与实现二部图最大匹配（Bipartite Matching）问题的求解算法。*/
#include <algorithm>
#include <cstdio>
#include <list>
#include <queue>
#include <iostream>
using namespace std;
#define INFI 1000
typedef struct _mark
{
	int pre_suc;//前驱
	int max_incr;
}MARK;
int iteration = 0;//增广路径数目
const int N = 100;
list<int> setS;
bool isMark[N], isCheck[N], isDone;
MARK markList[N];
int c[N][N], f[N][N];
int n; //顶点数
int Maxflow()
{
	int flow = 0;
	for (int i = 0; i < n; i++)
	{
		flow += f[0][i];
	}
	return flow;
}
void Mincut()//isMark的点就是最小割
{
	int i = 0;
	while (i < n)
	{
		if (isMark[i])
			setS.push_back(i);
		i++;
	}
}
int IncrFlowAuxi(int index)//计算增广路径中的最大可增量
{
	if (index == 0)
		return markList[index].max_incr;
	int prev = markList[index].pre_suc;
	int maxIncr = markList[index].max_incr;
	return min(maxIncr, IncrFlowAuxi(prev));//递归求最大增量
}
void IncrFlow()//增广路径的增加
{
	iteration++;
	int incr = IncrFlowAuxi(n - 1); //最大可增量
	int index = n - 1;
	int prev;
	while (index != 0)
	{
		if (index != n - 1)
			cout << index << " ";
		prev = markList[index].pre_suc;
		f[prev][index] += incr; //增广路径增加后，更新流量
		index = prev;
	}
	cout << endl;
}
void Mark(int index, int pre_suc, int max_incr)
{
	isMark[index] = true;
	markList[index].pre_suc = pre_suc;
	markList[index].max_incr = max_incr;//当前路径的流值
}
void Check(int i)//被mark且被check的点表示已经被纳入新路径
{
	isCheck[i] = true;
	for (int j = 0; j < n; j++)
	{
		if (c[i][j] > 0 && !isMark[j] && c[i][j] > f[i][j])//forward 边
			Mark(j, i, min(markList[i].max_incr, c[i][j] - f[i][j]));
		if (c[j][i] > 0 && !isMark[j] && f[j][i] > 0)//reverse 边
			Mark(j, i, min(markList[i].max_incr, f[j][i]));
	}
}

int ford_fulkerson()
{
	int i;
	while (1)//一次循环找到一个新路径
	{
		isDone = true;
		i = 0;
		while (i < n)//判断上次循环是否有找到新路径
		{
			if (isMark[i] && !isCheck[i])  //判断是否所有标记的点都已被检查
			{
				isDone = false;
				break;
			}
			i++;
		}
		if (isDone) //计算最小割和最大流
		{
			Mincut();
			return Maxflow();
		}
		while (i < n)//贪心法构建新路径
		{
			if (isMark[i] && !isCheck[i]) {
				Check(i);
				i = 0;
			}
			if (isMark[n - 1]) //如果汇t被标记，说明找到了一条增广路径，则增加该条路径的最大可增加量
			{
				IncrFlow();
				memset(isMark + 1, false, n - 1); //增加该增广路径后，除了源s，其余标记抹去
				memset(isCheck, false, n);
			}
			else i++;
		}
	}
}
int main()
{
	n = 12;
	for (int k = 0; k < n; ++k)
	{
		memset(c[k], 0, sizeof(c[0][0])*n);
		memset(f[k], 0, sizeof(f[0][0])*n); 
		memset(isMark, false, n);
		memset(isCheck, false, n);
	}
	isMark[0] = true; 
	markList[0].max_incr = INFI;
	markList[0].pre_suc = INFI;
	c[1][6] = INFI;
	c[1][7] = INFI;
	c[2][7] = INFI;
	c[3][6] = INFI;
	c[3][8] = INFI;
	c[3][9] = INFI;
	c[4][7] = INFI;
	c[4][10] = INFI;
	c[5][7] = INFI;
	c[5][10] = INFI;
	for (int i = 1; i < n / 2; i++)
		c[0][i] = 1;
	for (int i = n / 2; i < n - 1; i++)
		c[i][n - 1] = 1;
	cout << "最大匹配结果为：" << endl;
	int result = ford_fulkerson();
	cout << "匹配边个数为：" << result << endl;
	system("PAUSE");
}

package 项目选择;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Arrays;

public class ProjectSelection {
		public static final int INFI=1000;
	    public static void main(String[] args) {

	       int[][] c1=new int[][]{
	    	   {0,3,2,4,0,0,0,0},
	    	   {0,0,0,0,0,INFI,0,0},
	    	   {0,0,0,0,INFI,0,0,0},
	    	   {0,0,0,0,0,0,INFI,0},
	    	   {0,0,0,0,0,0,0,2},
	    	   {0,0,0,0,0,0,0,1},
	    	   {0,0,0,0,0,0,0,2},
	    	   {0,0,0,0,0,0,0,0}
	        };
	        MGraph1 m2=new MGraph1(c1);
	        m2.fordFulkerson(0, 7);
	    }
	}

	class MGraph1{
	    private int[][] c;        //容量矩阵
	    private int[][] e;        //残量矩阵
	    private int[][] f;        //当前流矩阵
	    private int vexNum;        //顶点数量
	    
	    public MGraph1(int[][] c){
	        this.c=c;
	        this.vexNum=c.length;
	        this.e=new int[vexNum][vexNum];
	        this.f=new int[vexNum][vexNum];

	        //刚开始时残量矩阵等于容量矩阵
	        for(int i=0;i<vexNum;i++){
	            System.arraycopy(c[i], 0, e[i], 0, c[i].length);
	        }
	        
	    }
	    public void fordFulkerson(int s,int t){
	        int[] route=new int[vexNum];    //s到t的路径数组,route[i]表示i的前一个顶点
	        
	        while(bfs(s,t,route)){             //若还能找到一条路径
	            
	            //寻找路径中流最小的边的大小(在残量矩阵中)
	            int min=Integer.MAX_VALUE;
	            int tail=t;
	            int head=route[t];

	            while(head!=-1){
	                if(e[head][tail]<min){
	                    min=e[head][tail];
	                }
	                tail=head;
	                head=route[head];
	            }        
	            
	            //更新当前流矩阵和残量矩阵
	            int tail1=t;
	            int head1=route[tail1];
	            while(head1!=-1){
	                //更新当前流矩阵
	                if(c[head1][tail1]!=0){        
	                    f[head1][tail1]+=min;        //容量矩阵中存在边,增加head1到tail1的流的大小为min
	                }else{
	                    f[head1][tail1]-=min;        //容量矩阵中不存在边，撤销head1到tail1的流的大小为min
	                }
	                //更新残量矩阵
	                e[head1][tail1]-=min;            //head1到tail1的流量减少min
	                e[tail1][head1]+=min;            //tail1到head1的流量增加min
	                
	                tail1=head1;
	                head1=route[head1];
	            }
	          
	            Arrays.fill(route, 0);                 //初始化路径数组
	        }//while 还能找到一条s到t的路径
	        
	        int maxFlow=0;
	        for(int i=0;i<vexNum;i++)                //最大流为  当前流矩阵中  从s流出的量
	            maxFlow+=f[s][i];
	        int profit=9-maxFlow;
			System.out.println("最大收益为:"+profit);
	        
	        
	        System.out.print("选择项目为(集合S)：");
	        ArrayList<Integer> cut=cut(s);
	        for(int i=0;i<cut.size();i++)
	            System.out.print(cut.get(i)+" ");
	        System.out.println();
	        
	    }
	    
	    //广度优先搜索在残量图e中寻找s到t的路径
	    public boolean bfs(int s,int t,int[] route){
	        boolean[] visited=new boolean[vexNum];        //访问数组
	        visited[s]=true;
	        
	        ArrayDeque<Integer> queue=new ArrayDeque<>();
	        route[s]=-1;                                //设s的前一个顶点为-1
	        
	        for(int i=0;i<vexNum;i++){
	            if(e[s][i]!=0 && !visited[i]){            //在残量矩阵中s到i存在一条路径
	                queue.add(i);
	                route[i]=s;
	                visited[i]=true;
	            }
	        }
	        
	        while(!queue.isEmpty()){
	            int middleVex=queue.poll();
	            if(middleVex==t){
	                return true;
	            }else{
	                for(int i=0;i<vexNum;i++){
	                    if(e[middleVex][i]!=0 && !visited[i]){
	                        queue.add(i);
	                        route[i]=middleVex;
	                        visited[i]=true;
	                    }
	                }
	            }
	        }
	        return false;
	    }
	    
	    //求最小割
	    //在残量矩阵中,从s开始做一次搜索,从s能达到的所有的顶点都属于集合S
	    public ArrayList<Integer> cut(int s){
	        boolean[] visited=new boolean[vexNum];
	        ArrayList<Integer> cut=new ArrayList<>();    //保存最小割,集合S
	        dfs(visited,cut,s);
	        return cut;
	    }
	    //深度优先搜索
	    private void dfs(boolean[] visited,ArrayList<Integer> cut,int v){
	        cut.add(v);
	        visited[v]=true;    
	        for(int i=0;i<vexNum;i++){
	            if(e[v][i]!=0 && !visited[i]){
	                dfs(visited,cut,i);
	            }
	        }
	    }
	}

#include<queue>
#include<iostream>
#include<string.h>
using namespace std;
#define MAX 1024
int nodes, edges;

int capacity[MAX][MAX];//记录边的当前还可以通过的最大流量
int maxflow = 0;
bool isVisited[MAX];
int pre[MAX];


inline int min(int a, int b)
{
	return a > b ? b : a;
}



bool BFS()
{
	queue<int> myQueue;
	myQueue.push(0);
	isVisited[0] = true;
	pre[0] = -1;
	while (!myQueue.empty())
	{
		int current = myQueue.front();
		myQueue.pop();
		for (int i = 0; i < nodes; i++)
		{
			if (!isVisited[i] && capacity[current][i])
			{
				myQueue.push(i);
				pre[i] = current;
				isVisited[i] = true;
			}
		}
	}

	return isVisited[nodes - 1];
}

void MaxFlow()
{
	while (1)
	{
		memset(isVisited, false, nodes);
		memset(pre, 0xff, 4 * nodes);

		//  if(!DFS(0))
		//      break;
		if (!BFS())
			break;

		int increase = MAX;
		int i;
		for (i = nodes - 1; pre[i] >= 0; i = pre[i])
		{
			increase = min(increase, capacity[pre[i]][i]);
		}
		for (i = nodes - 1; pre[i] >= 0; i = pre[i])
		{
			capacity[pre[i]][i] -= increase;
			capacity[i][pre[i]] += increase;
		}
		maxflow += increase;


	}
}
int main()
{
	while (1)
	{
		cout << "vexs edges:" << endl;
		cin >> nodes >> edges;
		int firstnode, secondenode, capa;
		for (int i = 0; i < edges; i++)
		{
			cin >> firstnode >> secondenode >> capa;
			capacity[firstnode][secondenode] = capa;
		}
		MaxFlow();
		cout << "最大流：" << maxflow << endl;
		maxflow = 0;

	}
	return 0;
}

算法概论上机集合

猜你喜欢