原作者：Tai-Danae Bradley

原文地址: https://www.math3ma.com/blog/matrices-probability-graphs

请在电脑上阅读本文

今天我想分享一个想法。一个非常简单的想法。它不是花哨的，也不是新的。事实上，我相信很多人已经考虑过这个问题了。但如果你没有或者即使你有 - 我希望你花几分钟时间和我一起感受它所带来的乐趣：把每个矩阵看成一个图。

很简单！但是我们可以从中获得很多好处。

首先，我会更精确一点：每个矩阵对应一个加权的二分图。 “图形”是指顶点（点）和边的集合; 所谓“二分”是指点有两种不同的类型/颜色; 所谓“加权”是指每个边都用数字标记。

在上图中左边的矩阵M是一个3×2的矩阵(3行2列)，它对应于右边的一个图形，其中我画了3个绿色的点,它们分别代表左边矩阵M的3行，2个粉色的分别代表矩阵M的2列。我还在绿色点和粉色点之间画上了一条边，它们表示矩阵M中的非空元素,边上的数字表示对应的非空元素值。

举例来说, 上图中第2绿色的点和第1个粉色的点之间有一条边（边上有数字4）,这是因为 $M_{21}$ ＝ 4,即M的第2行第1列的元素值是4,它是非空元素。在所有非空元素的位置上我都会画上一条边。另一方面,如果两个点之间没有边相连则表示这两个点所对应的矩阵元素是空值,即0。如上图中第1个绿色点与第2个粉色点之间没有边存在,这是因为 $M_{12}$ ＝0,即M的第1行第2列元素是0.

请允许我把一些通用的设置描述的更明确一些。

任意一个矩阵M都是一个包含n × m个元素的数组。这并不新鲜，但是这样一个数组也可以被看作是一个函数。M:X×Y $\rightarrow$ $\mathbb{R}$ 且X={ $x_{1}$ ,…, $x_{n}$ }是一个包含n个元素的集合, Y={ $y_{1}$ ,…, $y_{m}$ }是一个包含m个元素的集合。实际上，如果我想向你描述矩阵M，那么我需要告诉你M中每个元素是什么(即第i行,第j列位置上的元素值)。换句话说，对于任意下标(i,j)的位置，我需要告诉你它所对应的元素值 $M_{i,j}$ ,这恰恰是函数所做的。一个函数M：X×Y $\rightarrow$ $\mathbb{R}$ 和每一对( $x_{i}$ ， $y_{i}$ )矩阵元素M( $x_{i},y_{i}$ )相关联。(如果你喜欢也可以删除那些字母只用(x,y)来表示),如可以简写成用M(i,j)来表示M( $x_{i},y_{i}$ )。

瞧瞧。矩阵就是一个函数。

正如我们所定义的那样,让我们进一步思考一下,这里X的元素被标记为绿色,Y的元素被标记为粉色。于是矩阵M对应于以下方式的一个“加权二分图”: 图中的点由两种不同颜色的点X和Y组成。如果点 $x_{i}$ 和点 $y_{i}$ 之间有一条边则表示矩阵元素 $M_{i,j}$ 是一个非零值，如果 $M_{i,j}$ 的值是零，则点 $x_{i}$ 和点 $y_{i}$ 之间没有边相连。

所以，我们可以把每一个矩阵看成一张图。

当我们把矩阵可视化成一张图时奇妙的事情就会发生，请看:

矩阵乘法变成了路径的遍历

如果给你两个矩阵(图)M：X×Y $\rightarrow$ $\mathbb{R}$ 和N：Y×Z $\rightarrow$ $\mathbb{R}$ ,当我想要做这两个矩阵的乘法运算时，我们可以拼接这两个矩阵图，然后沿着拼接后的路径行进：乘积矩阵MN的第(i,j)个元素的值是由连接点 $x_{i}$ 和 $z_{i}$ 的所有边的权重值相乘,然后累加后得到的例如:

对称矩阵对应于对称图

如果一个矩阵和其转置矩阵相等,则称为对称矩阵，我们可以清楚的看到对称矩阵的元素总是沿着主对角线呈对称分布。然而我们也可以在图中看到这种对称性。特别的，我们可以从图中清晰的看到，对于任意矩阵M,它的 $MM^{T}$ 和 $M^{T}M$ 矩阵也是对称的。

不含有零元素的矩阵对应于全连接的“二分图”

如果一个矩阵不含有零元素，那该矩阵所对应的二分图中将没有缺失的边，也就是说X的顶点集合中的每一个点将会连接Y顶点集合中的每一个点，这样的二分图称为全连接二分图。

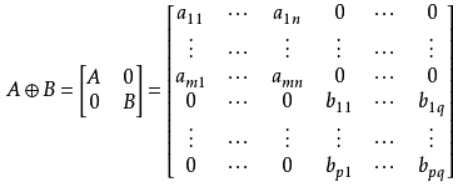
块矩阵对应于一个断开的二分图

比较特别的是，当两个矩阵做“直和”运算后产生的块矩阵对应于一个断开的二分图。两个矩阵做直和运算时它们会被分别堆积在块矩阵的左上角和右下角的位置（直和运算不像一般的矩阵和向量的加法那样对应元素相加），直和运算的结果是生成一个包含大量0元素的块矩阵。通过将原始矩阵的两个二分图堆叠在一起来获得块矩阵的二分图。

我们可以谈论更多的矩阵和图的内容，但我想从另外一个方向来进行我们的讨论。事实证明，概率非常适合我们的矩阵图讨论。它可以通过一个漂亮的小例子来实现的：

例如:

这样的概率分布的图使我们能够发现一些有趣的东西。

联合概率

通过构造,图中的边捕获了联合概率:( $x_{i},y_{i}$ )的联合概率作为权重值被标注在连接这两个点的边上面。

(上图中x1和y2之间并没有边相连,故P(x1,y2)=0)

边缘概率

边缘概率是通过沿着矩阵的行/列求和得到的(等效于上图)。例如 $x_{1}$ 的边缘概率 $P(x_{1})$ = $P(x_{1},y_{1})$ + $P(x_{1},y_{2})$ =1/8+0,也就是矩阵第一行的和。同样y2的边缘概率P(y2)=P(x1,y2)+P(x2,y2)+P(x3,y2)=0+1/8+1/4,也就是矩阵第二列求和。

在二分图中, $x_{i}$ 的边缘概率是所有连接顶点 $x_{i}$ 的边的权重值求和。类似的， $y_{i}$ 的边缘概率是所有连接顶点 $y_{i}$ 的边的权重值求和.

条件概率

条件概率是通过一个联合概率除以一个边缘概率而得到的。例如给定y2求x3的条件概率P(x3|y2)=P(x3,y2) / P(y2),在二分图中，条件概率的值为连接(x3,y2)这两个点的边的权重值除以连接y2点所有边的权重值之和。同样 $P(y_{i}|x_{i})$ 的概率是连接( $y_{i},x_{i}$ )这两个点的边的权重值除以连接 $x_{i}$ 的所有边的权重值之和。

很简单吧？

这里没有任何复杂的东西，但有时候以新的方式看待旧的想法真是太好了！

关系就是矩阵

我将用附录来结束这篇文章 - 另一个我觉得非常令人愉快的简单的事实是：矩阵算法对交换环有意义。不只是像 $\mathbb{R}$ (实数集)或 $\mathbb{C}$ (复数集)。事实上，它变得更好。你甚至不需要负数来乘以矩阵：矩阵算术对于可交换的半环是有意义的！（半环是没有添加反转的环。）

我认为这是非常有趣的，因为带有两个元素 $\mathbb{Z}_{2}$ ={0,1}的集合形成了一个带有以下加法和乘法运算的半环：

为什么这么棒？因为一个矩阵M ：X × Y → $\mathbb{Z}_{2}$ 表现为一种关系，这个关系只是X × Y的笛卡尔积的一个子集R的名称。换句话说每一个 $\mathbb{Z}_{2}$ 矩阵定义了一个关系，而每一个关系也定义了一个 $\mathbb{Z}_{2}$ 矩阵，其中: $M_{ij}$ =1 当且仅当每对( $x_{i},y_{i}$ )是子集R的一个元素，当 $M_{ij}$ =0时除外。

上面的 $\mathbb{Z}_{2}$ 矩阵与上面的二分图完全相同，不同的是二分图的权重要么是1，要么是0，如果是0我们就不会画出这两个顶点之间的边（我们称为关系二分图）。

(顺便说一下，你现在或许要问,“因为每个关系对应与一个 $\mathbb{Z}_{2}$ 矩阵，那么对应与等价关系的矩阵是什么?”,但是，我们离题了...)

通过改变底层（半）环从 $\mathbb{R}$ 至 $\mathbb{Z}$ ，我们改变了我们解释权重的方式。例如，在上面的概率场景中，我们或许要问，“从x1 至 y1我们获得的概率是多少？在之前那个例子(二分图中,连接(x1,y1)的边上的权重是1/8)所以概率是1/8=12.5%。或者,当矩阵是 $\mathbb{Z}_{2}$ 矩阵时,我们的问题变成：事件x1和事件y1同时发生是否可能？得到的答案是yes,如果连接(x1,y1)的边的权重是1，如果权重是0，则x1和y1不可能同时发生。

很棒的是，关系的组成恰恰是使用 $\mathbb{Z}_{2}$ 的矩阵乘法运算。换句话说给定两个关系R⊂X×Y 和 S⊂Y×Z，那么会有一个新的关SR⊂X×Z它由所有的(x,z)对所组成。这样至少存在一个y∈Y with (x,y) ∈R and (y,z)∈S.这种新关系正是由表示R和S的矩阵的乘积所指定的。

关于矩阵/关系的这个小事实绝对是我最喜欢的数学事实列表中的首要问题,一个原因是因为有限集和关系的类别很像有限向量空间和线性映射的类别。实际上，它更像是有限维希尔伯特空间( finite-dimensional Hilbert spaces)的范畴。这意味着许多看似完全不同的想法突然变得密切相关。这些联系可以更精确，这是一个经常在类别理论界共享的故事。希望我也可以在博客上分享它。

我认为，关系往往不被重视。在高中学的数学，我了解到函数非常重要。他们说, “每项输入的作业必须只有一个输出，” 没有人提到有关多输出的任何内容。每当这种异常确实出现时，它通常表现为异常和禁区。但关系应该得到更好的待遇！一个原因是因为关系是将线性映射设置为向量空间。线性代数中有很多精华，因此关系中也有很多精华。简而言之，关系是非常优秀的公民。

由于本人水平有限，如有不理解的地方请参考原文:https://www.math3ma.com/blog/matrices-probability-graphs

有趣的矩阵与概率的图形化表示