6旋转数组的最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
分析:二分查找变种,没有具体的值用来比较。那么用中间值和高低位进行比较,看处于递增还是递减序列,进行操作缩小范围。
-
处于递增:low上移
-
处于递减:high下移(如果是
high-1,则可能会错过最小值,因为找的就是最小值) -
其余情况:low++缩小范围
public class RotateArray {
public static void main(String[] args) {
RotateArray roatearray = new RotateArray();
int[] array = {3,4,5,2,3};
int min = roatearray.minNumberInRotateArray(array);
System.out.println(min);
}
public int minNumberInRotateArray(int [] array) {
int low = 0;
int high = array.length-1;
int mid = 0;
while(low < high) {
if(array[low] < array[high]) {
return array[low];
}
mid = low + (high -low) / 2;
if(array[low] < array[mid]) {
low = mid + 1;
}else if(array[mid] < array[high]) {
high = mid;
}else
low++;
}
return array[low];
}
}
7Fibonacci数列
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0,第1项是1)。n<=39
1. 递归法
分析
斐波那契数列的标准公式为:F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3,n∈N*)
2.优化递归
分析
递归会重复计算大量相同数据,我们用个数组把结果存起来8!
3. 优化存储分析
其实我们可以发现每次就用到了最近的两个数,所以我们可以只存储最近的两个数
- sum 存储第 n 项的值
- one 存储第 n-1 项的值
- two 存储第 n-2 项的值
public class fibonacci {
public static void main(String[] args) {
fibonacci fib = new fibonacci();
int res = fib.Fibonacci3(39);
System.out.println(res);
}
//递归 时间复杂度 O(2^n) 空间复杂度O(1)
public int Fibonacci1(int n) {
if(n <=1) {
return n;
}
return Fibonacci1(n-1) + Fibonacci1(n-2);
}
//优化递归 递归每一次都会计算大量的数据,可以将之前计算的数据存储在数组中
// 时间复杂度 O(n) 空间复杂度O(1)
public int Fibonacci2(int n) {
int[] arr = new int[40];
arr[0] = 0;
arr[1] = 1;
for(int i =2; i <= n; i++) {
arr[i] = arr[i-1] + arr[i-2];
}
return arr[n];
}
//优化存储 two代表第n-2的值 one代表第n-1的值
public int Fibonacci3(int n) {
int two = 0;
int one = 1;
int sum = 0;
for(int i = 2; i <= n; i++) {
sum = two + one;
two = one;
one = sum;
}
return sum;
}
}
8 跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
分析:
本质上还是斐波那契数列,所以迭代也可以求
当成 dp 问题来想的话:首先分析问题,它最终解是由前面的解累积起来的解,如何缩小问题的规模?
首先可知,第一阶有只能一步,一种;,第二阶可以两次一步、一次两步两种
- 若楼梯阶级 n = 3
- 跳 2 步到 3:剩下的是第一步没跳,起始跳到第一步只有一种
- 跳 1 步到 3:剩下的是第二步没跳,起始跳到第二步有两种
通过分类讨论,问题规模就减少了:
- 若楼梯阶级 n = n
- 跳 2 步到 n:剩下的是第 n - 2 步没跳,起始跳到第 n - 2 步设它为 pre2 种
- 跳 1 步到 n:剩下的是第 n - 1 步没跳,起始跳到第 n - 1 步设它为 pre1 种
同时可以发现第 n 阶的解法,只要用到 n - 1 和 n - 2 阶是多少,其他的不用考虑,因此用两个变量临时存下来即可
dp(i) = dp(i-2) + dp(i-1)
public class stepJump {
public static void main(String[] args) {
stepJump stepjump = new stepJump();
int res = stepjump.JumpFloor(3);
System.out.println(res);
}
//可以使用Fibonacci 但不推荐
public int JumpFloor(int target) {
if(target <= 2) {
return target;
}
int two = 1;
int one = 2;
int cur = 0;
for(int i = 3;i <= target; i++) {
cur = two + one;
two = one;
one = cur;
}
return cur;
}
}
9变态跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
分析
f(n)=f(n-1)+f(n-2)+……f(1)
f(n-1)=f(n-2)+……f(1)
两式相减得
f(n)=2f(n-1)
而
f(1) = 1
所以
f(n) = pow(2, n - 1)
public class StepJump_9 {
public static void main(String[] args) {
StepJump_9 step = new StepJump_9();
int res = step.JumpFloorII(9);
System.out.println(res);
}
public int JumpFloorII(int target) {
if(target ==1) {
return target;
}
// return 2 * JumpFloorII(target -1);
return (int)Math.pow(2, target-1);
}
}
10矩形覆盖
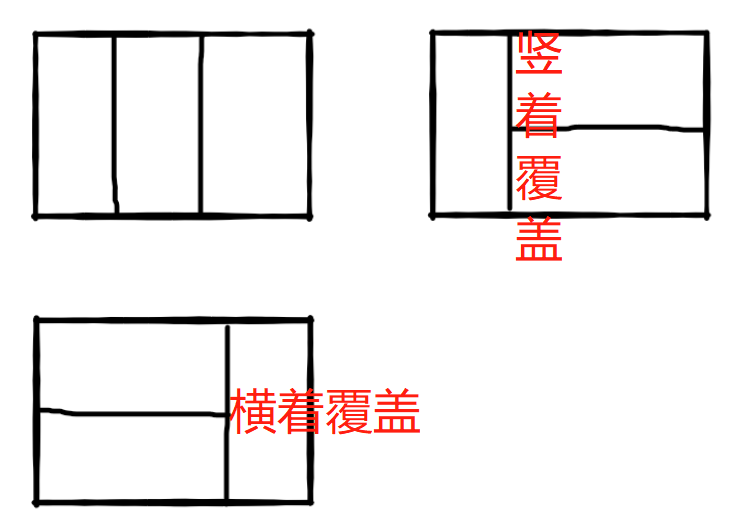
涂掉最后一级矩形的时候,是用什么方式完成的?
- n = 1 的时候
- 只能横着覆盖,一种
- n = 2 的时候
- 可以横着和竖着覆盖,两种
- n = 3 的时候
- 第三级横着覆盖,用了一级,剩下 n = 2,有两种覆盖方法
- 第三季竖着覆盖,用了两级,剩下 n = 1,有一种覆盖方法
- 总共有 3 种
- n = 4 的时候
- 第 4 级横着覆盖,用了一级,剩下 n = 3,有三种覆盖方法
- 第 4 级竖着覆盖,用了两级,剩下 n = 2,有两种覆盖方法
- 总共有 5 种方法
- n = n 的时候
- 第 n 级横着覆盖,用了一级,剩下 n = n - 1,所以关注第 n - 1 种有几种覆盖方法
- 第 n 级竖着覆盖,用了两级,剩下 n = n - 2,所以关注第 n - 2 种有几种覆盖方法
- 总和为两种情况的总和
所以回答上面的问题,涂掉最后一级矩阵的时候,可以选择使用横向完成,也可以使用竖向完成,横向涂剩下 n - 1 阶,竖向涂剩下 n - 2 阶
关注 n - 1 与 n - 2 时的涂法有几种,这就是斐波那契数列
public class rectangularFootprint_10 {
public static void main(String[] args) {
rectangularFootprint_10 rectangular = new rectangularFootprint_10();
int res = rectangular.RectCover(4);
System.out.println(res);
}
public int RectCover(int target) {
if(target <= 2) {
return target;
}
int two = 1;
int one = 2;
int cur = 0;
for(int i = 3; i <= target; i++) {
cur = two + one;
two = one;
one = cur;
}
return cur;
}
}