poj 1742 Coins 多重背包的可行性问题+优化讨论

部分引用来自《算法竞赛进阶指南》 lyd

首先我们从最简单的地方入手，多重背包不就是很多个01背包吗我们直接按01背包的套路来

$f[k]|=f[k-a[i]]$

于是我们~~如愿以偿~~的获得了超时

#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
ll a[102],c[102],f[100005];
int main(){
	int n,m;
	while(scanf("%d%d",&n,&m),n||m){
		memset(f,0,sizeof(f));
		for(int i = 1; i <= n; i++) scanf("%lld",&a[i]);
		for(int i = 1; i <= n; i++) scanf("%lld",&c[i]);
		f[0]=1;
		for(int i = 1; i <= n; i++)
		for(int j = 1; j <= c[i]; j++)
		for(int k = m; k >= a[i]; k--){
			f[k]|=f[k-a[i]];
		} 
		int ans = 0;
		for(int i = 1; i <= m; i++) ans+=f[i];
		printf("%d\n",ans);
	}
	return 0;
}

行了吧满意了有眼睛的都知道复杂度是 $\sum_{i=1}^{n} c[i]*(m-a[i])$ 这个量级就有点大了最多 100*1000*100000

不超时才怪吧

此时我们得搞点奇技淫巧了（行了我先睡觉了明天再说）

第一种优化思路：二进制拆分

我们知道   $2^{0},2^{1},2^{2},.....2^{k-1}$ 从这k个数中选若干个可以构成 0~2^k-1的任何数

利用这个性质我们找出一个最大整数p 这个p满足   $2^{p+1}-1<=C_{i}$ 即 $2^{0},2^{1},2^{2},.....2^{p}<=C_{i}$

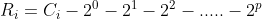
令 $R_{i}=C_{i}-2^{0}-2^{1}-2^{2}-.....-2^{p}$

利用p的最大性我们可以知道 $2^{0},2^{1},2^{2},.....2^{p}+2^{p+1}>C_{i}$ 所以 $R_{i}<2^{p+1}$ 因此 $2^{0},2^{1},2^{2},.....2^{p}$ 的若干个数相加可以得到0~Ri的任意数

从 $2^{0},2^{1},2^{2},.....2^{p},R_{i}$ 中选出若干个相加，可以表示出 Ri~Ri+2^(p+1)-1之间的任何数，又 $R_{i}+2^{p+1}-1=C_{i}$ 因此从 $2^{0},2^{1},2^{2},.....2^{p},R_{i}$ 中选出若干个相加可以表示出Ri~Ci之间的任何整数

综上所述：我们可以把数量为Ci的第 i 件物品拆分成 p+2 件物品它们的体积分别为

$2^{0}*V_{i},2^{1}*V_{i},....2^{p}*V_{i},R_{i}*V_{i}$

显然这 p+2 个物品可以凑出  0~Ci*Vi 之间所有能被V整除的数，并且不能凑出大于 Ci*Vi 的数，与原问题等价。

这样就把物品的数量下降到了 logCi级别的复杂度大大降低

以下代码C++T了 G++能过（poj老有这种玄学问题）

#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
int a[102][12],c[102],p[12];
bool f[100005];
int main(){
	int n,m;
	p[0]=1;
	for(int i = 1; i <= 11; i++) p[i]=p[i-1]*2;
	while(scanf("%d%d",&n,&m),n||m){
		memset(f,false,sizeof(f));
		for(int i = 1; i <= n; i++) scanf("%d",&a[i][0]);
		for(int i = 1; i <= n; i++) scanf("%d",&c[i]);
		for(int i = 1; i <= n; i++){
			int tot = 0;
			ll x = c[i];
			for(int j = 0; j <= 11; j++){
				if(x>=p[j]) a[i][++tot]=p[j]*a[i][0],x-=p[j];
				else break;
				//printf("i=%d j=%d p[j]=%lld x=%lld\n",i,j,p[j],x);
			}
			if(x) a[i][++tot]=x*a[i][0];
			c[i]=tot;
		}
		/*for(int i = 1; i <= n; i++)
		for(int j = 1; j <= c[i]; j++){
			if(j==c[i]) printf("a[i][j]=%lld\n",a[i][j]);
			else printf("a[i][j]=%lld ",a[i][j]);
		}*/
		f[0]=1;
		for(int i = 1; i <= n; i++)
		for(int j = 1; j <= c[i]; j++)
		for(int k = m; k >= a[i][j]; k--){
			f[k]|=f[k-a[i][j]];
		} 
		int ans = 0;
		for(int i = 1; i <= m; i++) ans+=f[i];
		printf("%d\n",ans);
	}
	return 0;
}

第二种优化思路：可行性优化

我们发现这个问题不同于普通的背包问题，这个题并没有价值这一个维度，只要求哪一些体积V是可以达到的，这是一个可行性问题而不是最优性问题。

我们发现对于前 i 种硬币能拼成的面值 j ，只有两种情况

前 i-1 种就能拼成面值 j ,即F[ j ]在第 i 阶段开始前就已经是true了

使用了第 i 种硬币后F[ j ]变为了true，即F[ j - a[ i ] ]为true,从而F[ j ]变为true

于是我们考虑一种贪心策略：

用used[ j ]表示F[ j ]在阶段 i 时为true至少要用多少枚第 i 种硬币，并且尽量选择第一种情况。也就是说如果F[ j - a[ i ] ] 为true时，如果F[ j ] 已经为true了，那我们不转移，并且令 used[ j ] = 0。否则我们执行 F[ j ] = F[ j ] 或者 F[ j ] = F[ j - a[ i ] ]的转移，并且在后者情况下令 used[ j ] = used[ j - a[ i ] ] + 1;

我们采用多重背包的方法对一个物品进行多次选择，并用used数组控制数量上限可以 O（N*M）的最低复杂度完成这道题目

#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
int a[102],c[102],used[100002];
bool f[100005];
int main(){
	int n,m;
	while(scanf("%d%d",&n,&m),n||m){
		memset(f,false,sizeof(f));
		for(int i = 1; i <= n; i++) scanf("%d",&a[i]);
		for(int i = 1; i <= n; i++) scanf("%d",&c[i]);
		f[0]=1;
		for(int i = 1; i <= n; i++){
			for(int j = 0; j <= m; j++) used[j]=0;
			for(int j = a[i]; j <= m; j++){
				if(!f[j]&&f[j-a[i]]&&used[j-a[i]]<c[i]) 
				f[j]=true,used[j]=used[j-a[i]]+1;
			}
		}
		int ans = 0;
		for(int i = 1; i <= m; i++) ans+=f[i];
		printf("%d\n",ans);
	}
	return 0;
}

第三种优化思路：单调队列优化（等我会了再说嘿嘿嘿）

lszxj13141314

原创文章 85 获赞 103 访问量 2499

关注私信

poj 1742 Coins 多重背包的可行性问题+优化讨论

猜你喜欢