引言
本文是吴恩达深度学习第一课:神经网络与深度学习的笔记。神经网络与深度学习主要讨论了如何建立神经网络(包括一个深度神经网络)、以及如何训练这个网络。
第一课有以下四个部分,本文是第二部分。
- 深度学习概论
- 神经网络基础
- 浅层神经网络
- 深层神经网络
(一不小心又写了2万字,想不到第二部分有这么长。)
学完了第二部分我们会用逻辑回归来实现一个图像识别算法。
二分类
本篇通过逻辑回归来阐述,逻辑回归是一个可用于二分类问题的算法。

以图像识别为例,假设我们有个64*64的图像,作为输入,输出就是该幅图像中是否包含猫。

计算机保存一张(彩色)图片,要保存三个独立矩阵,分别对应RGB(红绿蓝)三个颜色通道(Channel)。
如果输入的图像是6464像素的,那么就有3个6464的矩阵,分别对应RGB三种像素的亮度。
(为了演示方便,这里其实是54的,而不是6464的)
那如何用特征向量表示这幅图像呢?

像上面这样定义一个特征向量
x,把所有的像素值都取出来,例如红色里面的255、231,以及绿色里的255、134和蓝色里面的255、134。
这样就得到了一个很长的列向量,包含了3个通道所有的元素。这里是
3×64×64=12288维的列向量。
我们用
n或
nx=12288来标书输入的特征向量
x的维度。
在二分类问题中,我们输入这个
x,期望得到的输出是这个图片中是(1)否(0)有猫。
这里对一些记号进行说明。

我们常用
(x,y)表示一个单独的样本,
x∈Rnx说的是
x是
nx维的特征向量。
标签
y∈{0,1}
训练集的大小记为
m,
(x(1),y(1))表示第一个训练样本,注意数字在上标的位置,表示样本的编号,如果在下标的位置则表示特征(维)的编号。
mtrain表示训练集的样本数量;
mtest表示测试集的样本数量。

为了更紧凑的表示,用大写的
X表示整个数据集,这里将单一样本放到这个矩阵列的位置。因此就有
m列,
nx行。
有时也会将样本放到行的位置,但是在构建神经网络的时候,用前者会使得构建过程简单很多。
X∈Rnx×m是一个
nx×m(矩阵的表示是行
× 列)的矩阵。
因为这里的输出只有一个,要么是0要么是1。将它们放到一行中即可。

逻辑回归
已经了解了逻辑回归的读者可以跳过这一小节。
给定一副通过特征向量
x表示的图像,通过逻辑回归算法来评估这幅图像中含有猫的概率
y^。
y^=P(y=1∣x)
逻辑回归中用到的参数有:
- 输入特征向量
x∈Rnx,
nx是特征的数量
- 训练标签
y∈{0,1}
- 权值
w∈Rnx (也就是说每个特征都会有一个权值)
- 偏差
b∈R
- 输出
y^=σ(wTx+b)
- Sigmoid函数
s=σ(wTx+b)=σ(z)=1+e−z1
为了让
y^得到
[0,1]的值,将
z=wTx+b的结果传入到sigmoid函数中即可。

Sigmoid函数的图像是这样的,它能将一个很大的值,不管是负的很大还是正的很大,压缩到
[0,1]之间,刚好符号概率的定义。
这里还有一点要指出的是对任何一个数取
ex得到的输出都是正的,这个可以保证不会有负的概率。
在神经网络编程中,我们通常把
w和
b分开,这也是为什么上面写的是
wTx+b
还有一种符号约定是添加一个额外的特征
x0=1,所以
x变成了
nx+1维的向量。并定义
θ0=b,定义
θ1⋯θn等于
w1⋯wn。因此,
y^=θTx(
θ和
x现在都是
nx+1维的向量了)

逻辑回归的损失函数
为了训练逻辑回归的参数
w和
b,我们需要定义一个损失函数(loss function)。
y^(i)=σ(wTx(i)+b),whereσ(z(i))=1+e−z(i)1
给定训练数据
{(x(1),y(1)),⋯,(x(m),y(m))},我们想要我们的预测输出
y^(i)尽可能等于真实输出
y(i)。
i表示第
i个样本。
损坏函数的作用是衡量预测输出和真实值有多接近。
那么逻辑回归的损失函数
L(y^(i),y(i))定义为:
L(y^(i),y(i))=−(y(i)logy^(i)+(1−y(i))log(1−y^(i)))
我们希望损失函数越小越好,说明输出值越接近真实值。
这个损失函数其实是两种情况写到一起了:
- 若
y(i)=1 则
L(y^(i),y(i))=−logy^(i) ,想要损失函数小,就是让
−logy^(i)尽可能小,也就是让
logy^(i)尽可能大,即
y^(i)尽可能大,而它最大不会超过
1,因此是希望它能尽可能接近
1;
- 若
y(i)=0 则
L(y^(i),y(i))=−log(1−y^(i)) ,想要损失函数小,就是让
−log(1−y^(i))尽可能小,也就是让
log(1−y^(i))尽可能小,即
y^(i)尽可能小,而它最小不会小过
0,因此是希望它能尽可能接近
0;
损失函数是在单个训练样本中定义的,它衡量了在单个训练样本上的表现。
下面我们要定义一个成本函数(cost function)
J(w,b)来衡量全体训练样本的表现
J(w,b)=m1i=1∑mL(y^(i),y(i))=−m1i=1∑m[y(i)logy^(i)+(1−y(i))log(1−y^(i))]
其实就是求所有样本损失函数值的均值,我们要得到使得上式最小的
w,b。
梯度下降法
下面我们将学习如何使用梯度下降法来学习训练集上的参数
w和
b。

这个图像中的
x轴和
y轴分别表示
w和
b,
y轴表示对应的成本函数的值。
实际上
w可以是高维数据,这里为了绘图方便,让
w为一个实数。
我们要做的就是找到一组
w和
b,使得
J(w,b)去全局最小值,可以看到成本函数是一个凸函数,这样我们就有可能找到全局最小值。
如何找呢,先要初始化一个
w,b,上图中已经标出。然后用梯度下降法来找到最小值。
梯度下降法会让这个点朝着最陡的下坡方向走一步,也就是下降最快的方向,如果没有达到最小值,则继续向下走一步,直到解决全局最优解。
为了展示梯度下降法的一些细节,这里先忽略
b,这样就可以画成二维图像,假设成本函数是这样的图像。

梯度下降的算法是这样的:

按照这个公式重复地更新
w直到
w收敛,即直到
w到达最小值附近。
这里的
α表示学习率,用来控制梯度下降法的步长,不能过大也不能过小。
dwdJ(w)是
J对
w的导数,代表
w的变化量。
我们在编程时约定dw表示这个导数。

假设初始值位于上图紫色点位置,导数就是函数在这个点的斜率,这里
w的导数为正值。
根据上面的计算公式,
w会变小,也就是向左边移动。

这样就能逐渐达到最小值点,如果
w初始化为左边。

那么导数将会是负的,根据公式
w会变大,也就是向右移动。当然这里都假定学习率的取值是合理的。
这样不管初始化在哪里,最终都能达到最小值。
我们这里忽略了
b,如果考虑
b的话,这两个参数应该同时更新,如下:
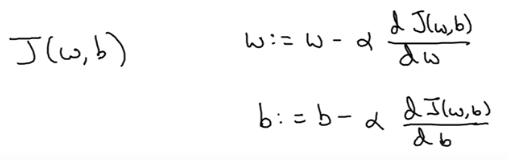
这里由求导数变成了求偏导数。

在编程时这两项可以用dw和db来表示。
计算图
一个神经网络的计算都是按照前向或反向传播过程来实现的。不了解的话没关系,后面会讲到的。
我们只要知道神经网络的输出,然后进行一个反向传播操作,就可以计算出对应的梯度,也就可以更新神经网络中的参数。
计算图可以很清晰的描述这个过程。
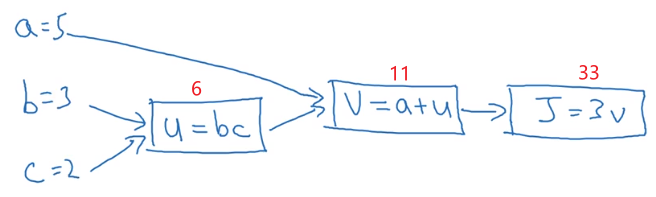
这里假成本函数为
J(a,b,c)=3(a+bc),首先用计算图来看一下是如何进行前向传播的。
这里可以简单的理解为 前向传播就是根据输入得到输出的过程;而反向传播是指根据输出求得参数的梯度过程。

要计算这个函数,实际上有三个不同的步骤。
- 第一步是计算
u=b×c,我们把
bc的结果存到
u中。
- 然后计算
v=a+u,即把
a+u的结果存到
v中。
- 最后计算输出就是
J=3×v
我们可以把这三个步骤化成计算图的形式:

假设
a=5,b=3,c=2,通过计算图的过程如下:
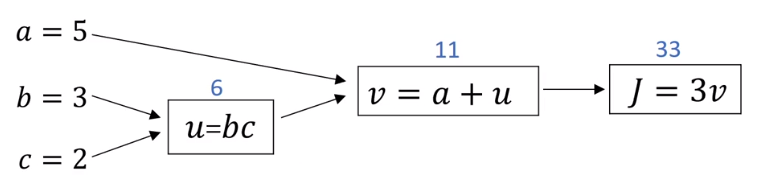
在逻辑回归中,
J是我们想要最小化的成本函数,通过计算图从左到右的过程,可以计算出
J的值。
计算图的牛逼之处就在于,通过计算图从右到左的过程,可以计算出每个输入参数对应的偏导数。

上图通过红色箭头画出来,和蓝色箭头正好相反。
下面我们就来看下如何计算导数。
假设你想计算
dvdJ,要怎么计算呢
J=3v,我们只要计算
J对
v的导数即可,
dvdJ=3,此时我们就完成了一步反向传播。
那
dadJ=?,这里要用到链式求导法,因为
v=a+u,从上图也可以看出来
a→v→J (
a影响了
v从而影响了
J)
所以
dadJ=dvdJdadv=3×1=3
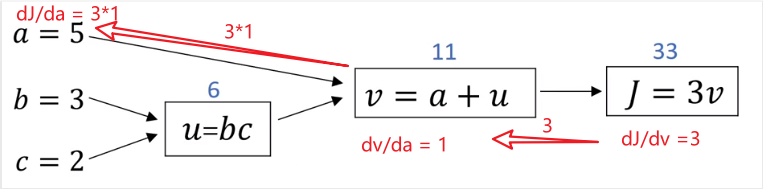
上面红色箭头就是求
dadJ的反向传播过程。我们在编程的时候约定用da表示
dadJ,用dv表示
dvdJ。
好了,上面只是完成了求
dadJ的反向传播路径,还剩下两个路径。
那么怎么计算
dudJ呢
和上面的过程一样,也是用链式求导法:
dudJ=dvdJdudv=3×1=3
因此我们计算出du=3。
那如何计算
dbdJ呢,这里
u=bc,再次运用链式法则得:
dbdJ=dudJdbdu=3×c=3×2=6
那这里的
c是什么呢,其实就是它的输入值
2,所以上式等于
6。
dcdJ留给读者朋友们自己去计算。
逻辑回归中的梯度下降法
本小节讨论如何求导,来实现逻辑回归的梯度下降算法。
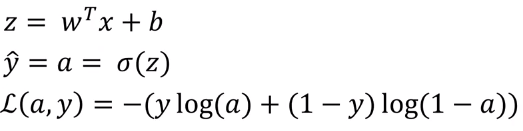
先来回顾下逻辑回归的相关公式,上面是考虑一个样本的情况。
假设我们的样本有两个特征
x1,x2,为了计算
z,我们需要权值
w1,w2和
b。

把它们都当成输入,放到计算图中,得到
z。
接下来就计算
y^。

也就是计算图的下一步,最后一步是计算损失函数
L(a,y)。

在逻辑回归中,我们要做的是改变参数
w和
b的值,来最小化损失函数。
我们可以通过计算图的前向传播来计算损失函数,现在我们主要来看下如果通过反向传播来计算偏导数。

要想计算
L对这些参数的偏导,我们需要先计算
L对
a的导数
dadL(代码中用da表示)。
这里的
log其实是
ln。
ln′a=a1
dad−(ylog(a)+(1−y)log(1−a))=−ay−1−a(1−y)⋅(−1)=−ay+1−a(1−y)
上面可以分成两个式子分别对
a求导即可。

现在可以继续计算出dz (
dzdL)
dzdL=dadLdzda
我们来求下
dzda
需用用到导数的四则运算,从人工智能数学基础之高等数学中截取部分出来:

先计算
(1−e−z)′(对
z求导数)吧,
(1−e−z)′=−(e−z)′=−(ez1)′=−(e−z)×(−1)=e−z(这里省去了把
−z看成一个整体)
dzda=dzdσ(z)=dzd1−e−z1=(1−e−z)20×(1−e−z)−1×(1−e−z)′=(1−e−z)2−e−z=(1−e−z)21−e−z−1=1−e−z1(1−e−z1−e−z−1)=1−e−z1(1−1−e−z1)=a(1−a)
(写的很详细了)
这里常数
1的导数是
0,
a=1−e−z1
最终可以得到
dzda=a(1−a)
现在可以继续计算
dzdL了:
dzdL=dadLdzda=(−ay+1−a(1−y))×(a(1−a))=−ay×(a(1−a))+1−a(1−y)×(a(1−a))=−y(1−a)+a(1−y)=−y+ay+a−ay=a−y
因此我们得到dz=a-y。

最后一步就是计算
dwdL和
dbdL(
x是样本,是已知量)
这里演示一下如何计算
dw1dL(dw₁)
dw1dL=dadLdzdadw1dz
dzdL=dadLdzda我们已经计算过了,这里要计算
z对
w1的偏导,计算
w1的偏导时,把
w2和
b看成常数:
dw1dz=dw1d(w1x1+w2x2+b)=x1
带入上面那个式子得:
dw1dL=dadLdzdadw1dz=(a−y)×x1
同理
dbdL=a−y
可以看到这个计算过程中
dzdL=dadLdzda是可以重复使用的。
对于给定的样本
x=(x1,x2),我们就可以通过下式来更新参数
w,b:

这就是单个样本的一次梯度更新步骤。
我们下小节就来看下如何更新整个数据集(m个样本)的梯度。
m个样本的梯度下降
要更新m个样本的梯度,我们由上面已经知道,先要写出成本函数
J。
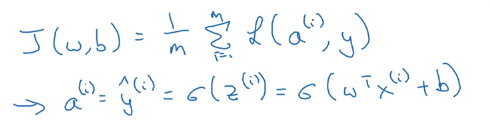
在上小节中,我们已经知道如何计算一个样本的梯度:
现在我们要计算所有(m个)样本的梯度。
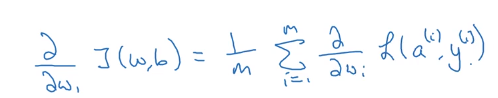
如果要计算成本函数
J对
w1的偏导数,就是要计算每个样本中损失函数
L对
w1的偏导数的均值。
下面用伪代码展示要如何做,我们先初始化参数值为零作为累加器。

我们对所有样本的累计值求均值,最终得到dw₁,dw₂,db之后我们就可以更新
w1,w2,b了。
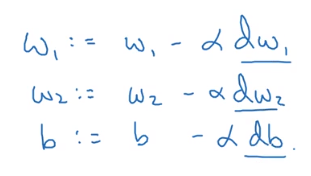
整个上面的过程只是一次迭代,我们可以重复这个步骤,直到参数值不再收敛,或者达到我们设定的迭代次数。
看起来不错,其实上面的过程有两个缺点。
要实现上面的代码需要编写两个for循环,第一个是for i=1 to m
第二个在这里,我们要遍历所有的特征,因为这里只有两个特征,可以直接写出来,如果有1000个特征,肯定要用循环了。
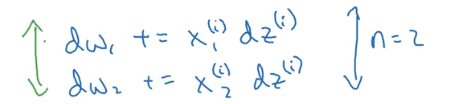
当我们应用深度学习算法时,如果在代码中显示的写for循环,会很低效。
那怎么办呢,是时候寻求向量化技术的帮助了。
下面我们就来了解下向量化。
向量化
什么是向量化(vectorizationi),其实就是将循环运算转换成向量运算。

在逻辑回归中,我们要计算
wTx,其中
w和
x都是
nx维的向量,如果不用向量化的话,可能会写成下面的循环:
Z = 0
for i in range(n_x):
z += w[i] * x[i]
z += b
如果用向量化的话,我们可以直接这么写:
z = np.dot(w,x) + b

下面通过代码向大家证明一下:

可以理解为,当有100万个样本时,向量化计算z只要1.5毫秒;而循环需要474毫秒。
python的numpy能充分利用CPU或GPU的并行化能力取更快的计算。
总之,能避免使用显示循环就避免。
下面来多看几个列子:

这个例子说向量与矩阵的乘法,如果用循环的话,就需要两个循环,而用向量化运算只要一段代码即可。

这是例子说,如果你想对向量中的每个元素都计算
ex,也是可以改成向量化形式的。
numpy中还有很多向量化操作,比如:

更多关于numpy以及向量化的知识可以参考numpy与matplotlib的使用简介。

上图就是我们上小节中计算梯度的代码,我们已经知道了这里面有两个for循环,我们如何用向量化的形式去掉这两个for循环呢。我们先来看下如何向量化第二个for循环。
这里我们要去掉dw₁,dw₂这种展开的写法,我们用一个向量dw来表示,我们知道权值
w的维度是
nx,因此我们可以这样初始化dw:
dw = np.zeros((n_x,1))
而计算dw的代码可以改成:
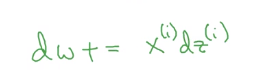
我们只向量化了第二个循环,因此上标的
i表示第
i样本,而这里
x(i)和
dz(i)都是代表向量。
最后得到的dw也是一个向量,只要除以m就得到均值了:
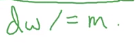
向量化逻辑回归
这小节我们就来探讨如何对整个逻辑回归的梯度下降算法进行向量化。
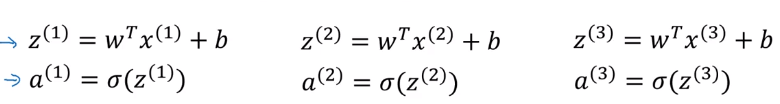
首先我们要对每个样本进行求
z和
a。
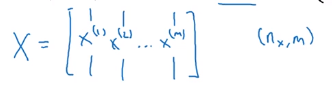
我们在上面二分类这一小节中看到过这样的
X表示,将样本按列放到矩阵
X中,这里有
nx行(特征数)和
m列(样本数)。
这里可能需要矩阵乘法相关知识,以下是人工智能数学基础之线性代数相关截图:

如果对求
z的过程向量化后,我们会用上面这种行向量
z来保存所有样本的结果,其中每个元素都是一个样本的结果。
就可以写成
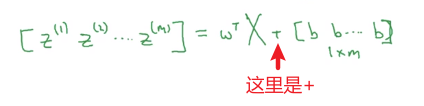
上面
wTX中的
wT是一个(
1×nx的)行向量,和
X展开就是这样的:
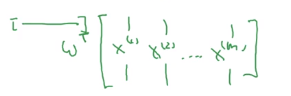
其实就是用
wT这一行去乘以
X的每列,得到
1×m的行向量。
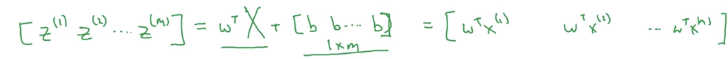
把偏置向量加进去就得:
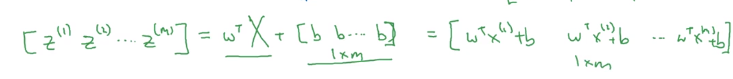
最后得到的就是其实就是
z(1),z(2),⋯,z(m)
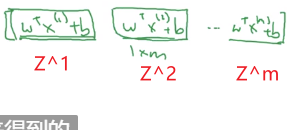
这里用大写的
Z来表示这个式子(其实这个结果是一个向量而不是矩阵,一般用小写字母表示向量,大写字母表示矩阵,如果后面看到代码中用z表示这个式子的结果请不要奇怪。)
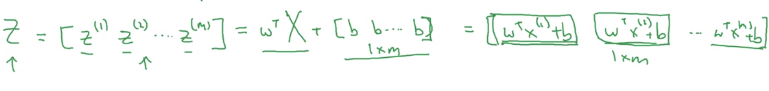
用代码实现起来很简单:
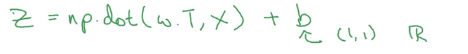
这里的b是个标量,numpy在进行相加是,会先把它扩展成
m×1的向量(广播),然后每个元素相加。
现在z求出来了,那如何求a呢?

其实很简单,这里用大小的
A来表示所有样本的结果,我们只要定义好
σ函数,把
Z带入即可,后面可以看到是如何编程实现的。
下面我们来看下如何向量化逻辑回归的梯度输出。
逻辑回归计算梯度过程的向量化
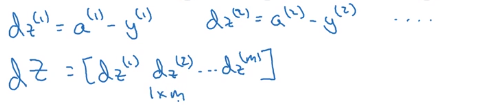
我们已经知道了如何求
dz(1),dz(2),⋯,dz(m)
现在用一个向量dZ来表示这些结果。
我们如何求出这个向量呢。
其实很简单,因为我们在上小节已经计算出了
A和
Y(这是真实标签,是已知的,表示为向量的形式即可)。
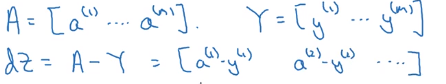
dZ就是
A−Y。
在向量化这一小节中,我们已经对dw进行向量化了,但是还是需要一个循环来遍历所有的样本,下面看如何去掉最后这个循环。
现在看下db:
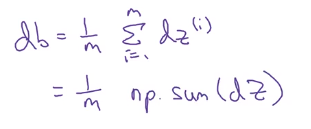
np.sum(dz)可以对dz向量和,然后除以样本总数。
实际上用db = np.mean(dz,axis=1)[0]也可以。
dw:
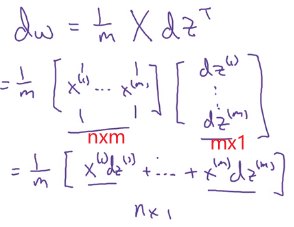
这样我们就去掉了所有的循环,下面就来看下向量化后的伪代码是怎样的:

广播
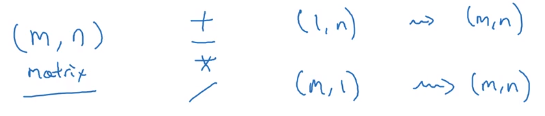
在python中,如果你用一个
m×n的矩阵与一个
1×n或
m×1的向量(矩阵)进行+,-,*,/,python首先将后面这个向量扩展成
m×n的形式,然后再逐个元素进行操作。
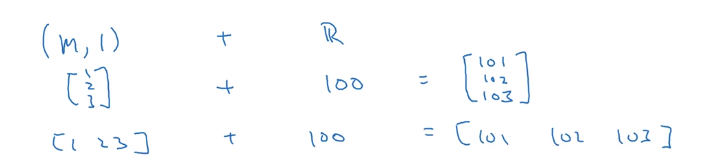
一个矩阵/向量 与 一个 标量进行运算也是一样的。
我们来看几个列子:
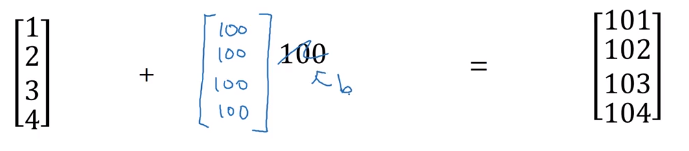
这里是一个向量与一个标量相加的例子,我们上一小节中的b就是这样的一个标量。
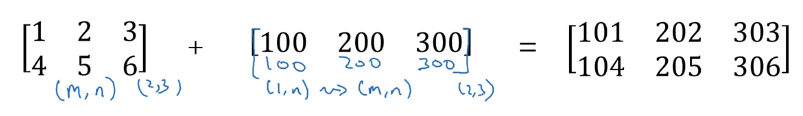
一个矩阵和一个行向量相加的例子。
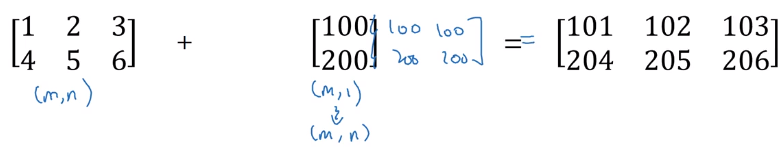
上面是一个矩阵和一个列向量相加的例子。
可以看到,这里其实有一定的规律。
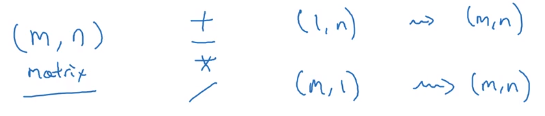
要么后面的向量中的列数n等于矩阵中的列数n,要么是行数m相等。
当然除了标量,标量是直接复制成
m×1的形式。
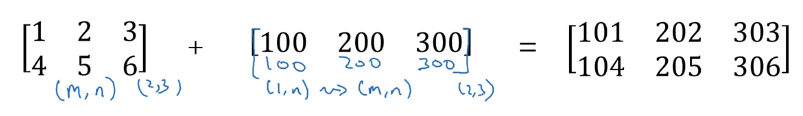
这里通过代码演示这种情况:

如果是下面这样会得到怎样的结果呢:

会报错,所以了解上面的规律很重要。
下面看一个例子,说的是100g不同的食物中的营养成分。

如果理解了上面说的广播内容,那么下面这个代码实现就不难了:

这个广播过程如果用代码写出来的话就是下面这样的:

关于numpy向量的说明
python numpy给我们提供了很高的灵活性,如上小节广播所示。
但是广播这么大的灵活性,有时会引入一些非常细微的错误,导致一些奇怪的bug。
比如我们把列向量与行向量相加,期望会报错说维度不匹配,但是实际上会得到一个列向量与行向量求和之后的矩阵。
下面分享一些技巧,可以排除这些奇怪的bug。
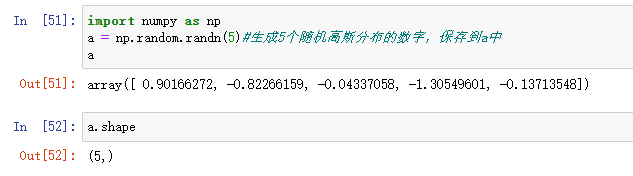
a.shape打印出来的是(5,)这种结构,这是python中秩为1的数组,既不是行向量也不是列向量。导致了它有一些不直观的效果。

比如它的转置得到本身。
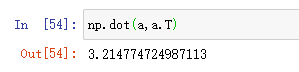
或者是np.dot(a,a.T),你可能会期望得到一个矩阵,实际上结果是一个数值。
因此建议在神经网络编程时不要使用这种结构。
这种情况下,我们可以使用a = np.random.randn(5,1),这样生成的就是一个列向量。

从输出可以注意到区别就是这里有两个方括号[[。

如果你得到了(5,)这样的结构,可以用a.reshape((5,1))来改成你想要的形状。

通过消除秩为1的数组,可以让我们的代码变得简单。
逻辑回归函数的解释
本小节来简要的证明下为什么逻辑回归成本函数的表达式是这样的。
y^(i)=σ(wTx(i)+b),whereσ(z(i))=1+e−z(i)1
在逻辑回归中,我们是这样定义
y^的。
我们约定
y^是给定
x的情况下
y=1的概率:
y^=P(y=1∣x),那么
y=0的概率就是
1−y^。
因为这里的
y要么是
0,要么是
1。
如果真实标签
y=1,那么在给定
x得到
y=1的概率就是:
P(y∣x)=y^,
如果
y=0,在给定
x得到
y=0的概率是:
P(y∣x)=1−y^
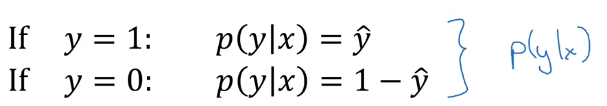
如果把上面这两个公式合成一起的话就是
P(y∣x)=y^y(1−y^)(1−y)
我们来分别看下
y=1和
y=0的情况。
如果
y=1,上式就变成了
y^;
如果
y=0,上式就变成了
1−y^;
都满足,所以我们可以这样合并。
我们在训练的时候,希望算法输出值的概率是最大的,也就是要
P(y∣x)最大化,
又因为
log函数是严格单调递增的函数,我们可以对这个概率取
log ,即
logP(y∣x)=logy^y(1−y^)(1−y)=ylogy^+(1−y)log(1−y^)
这就是我们损失函数的负值,而通常损失函数是求最小值的,因此我们加一个负号,就变成了求最小化。
那所有样本的成本函数要如何表示呢?
整个训练集中标签的概率可以写成如下:
P(labelsintrainingset)=i=1∏mP(y(i)∣x(i))
假设所有的训练样本服从同一分布且相互独立,上面就是这些样本的联合概率,就是每个样本的概率的乘积。
令这个概率最大化,等价于对其取对数最大化,即:
logP(labelsintrainingset)=i=1∑mlogP(y(i)∣x(i))
而上面说到
logP(y(i)∣x(i))=−L(y^(i),y(i)),这里我们想要最小化成本函数,也是加上个负号即可,这样就消掉了左边的负号。
得到了我们成本函数的表达式:
J(w,b)=i=1∑mL(y^(i),y(i))
最后为了对成本函数进行适当的缩放,除以样本总数
m。
J(w,b)=m1i=1∑mL(y^(i),y(i))
参考
(推荐网易云课堂,可以免费看并且还有课堂笔记。)
1. 吴恩达深度学习














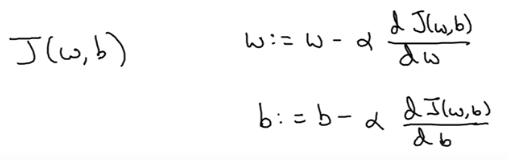







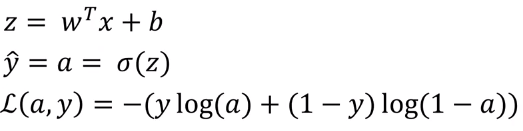








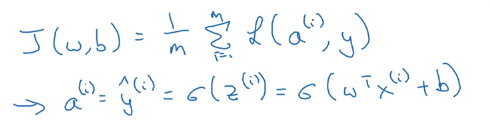
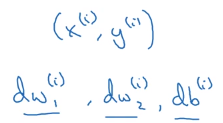
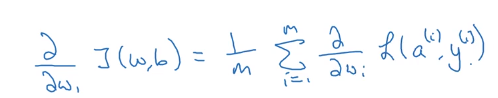

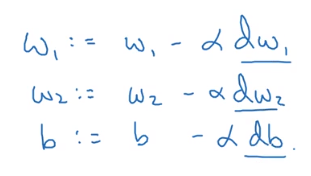
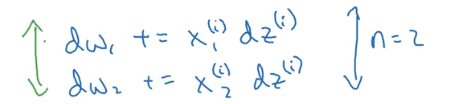







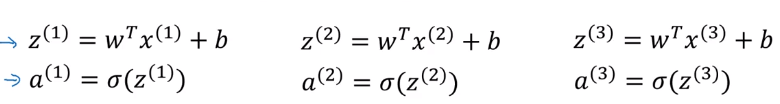
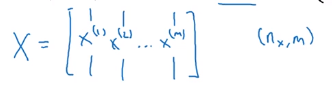
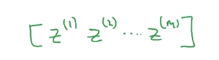

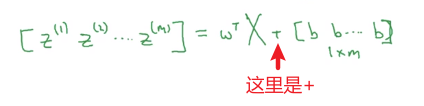
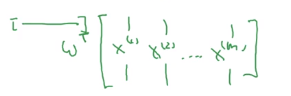
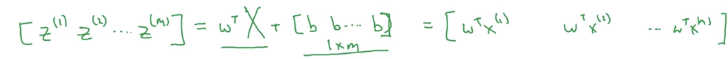
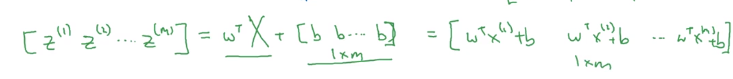
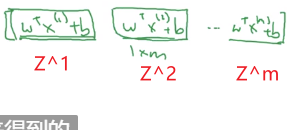
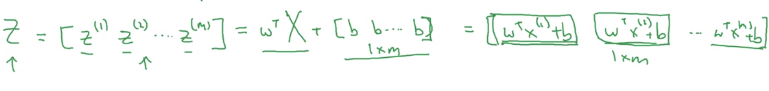
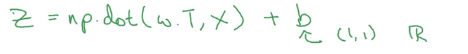

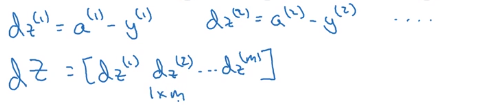
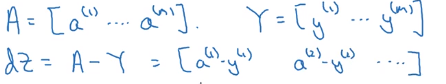
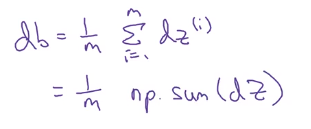
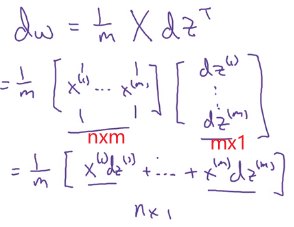

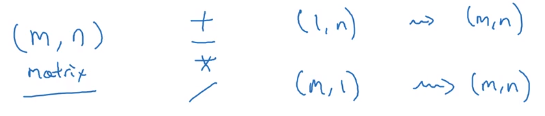
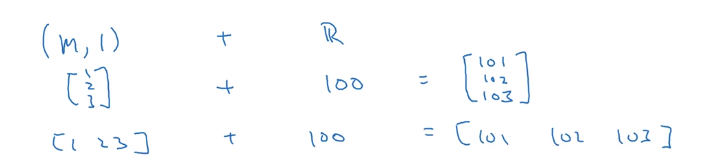
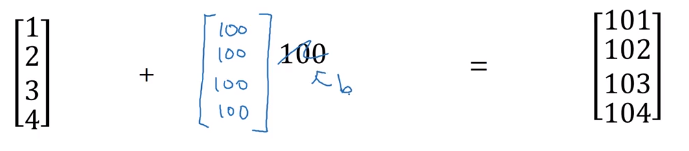
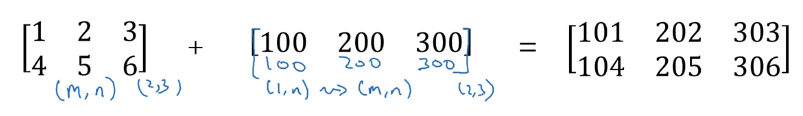
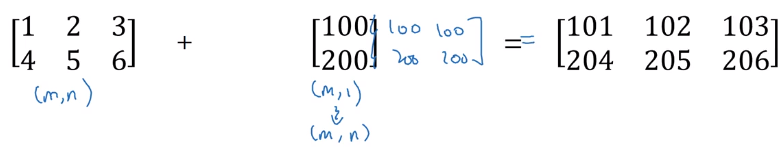
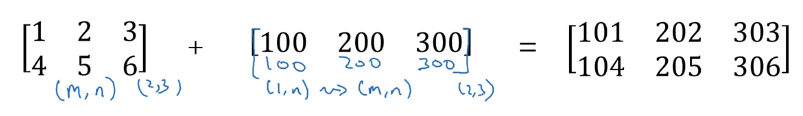












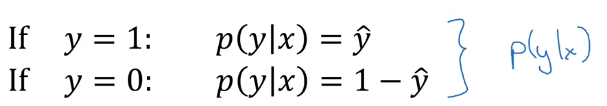

 博客专家
博客专家