混合高斯模型（Gaussian mixture model, GMM）及EM(Expectation-maximization algorithm)
1.原理
(1).多维变量X=(x1,x2,…xn)的联合概率密度函数为：
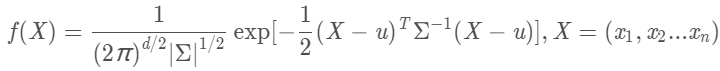
d:变量维度.
u:各维变量的均值
Σ：协方差矩阵，描述各维变量之间的相关度
(2).混合高斯模型
先从一个简单的例子开始：
随机选择1000名用户，测量用户的身高；若样本中存在男性和女性，身高分别 服从高斯分布N(μ1,σ1)和N(μ2,σ2)的分布，试估计参数:μ1,σ1,μ2,σ2; 如果明确的知道样本的情况(即男性和女性数据是分开的)，那么我们使用极大似然 估计来估计这个参数值。 如果样本是混合而成的，不能明确的区分开，那么就没法直接使用极大似然估计来 进行参数的估计。
假设混合高斯模型由K个高斯模型组成（即数据包含K个类），则GMM的概率密度函数如下:
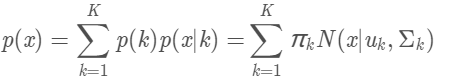
p(k)=πk是第k个高斯模型的权重，称作选择第k个模型的先验概率
若K=2，即两个成分混合，则式子如下:
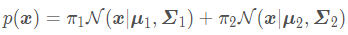
故，若信号含有两个分量，并以高斯混合模型对此进行建模后，问题便转变成了如何估计上述的六个参数π1,π2,u1,u2,Σ1,Σ2
(3).极大似然估计
极大似然估计(Maximum Likehood Estimate, MLE)（最大化对数似然函数）
似然函数数学化：设有样本集Y=y1,y2…yN. p(yn∣μ,Σ)是高斯分布的概率分布函数，表示变量Y=yn的概率。假设样本的抽样是独立的，那么我们同时抽到这N个样本的概率是抽到每个样本概率的乘积，也就是样本集Y的联合概率。此联合概率即为似然函数：
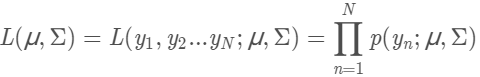
对数似然函数：
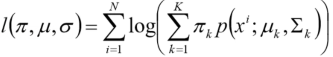
对式子进行求导并令导数为0，所求出的参数就是最佳的高斯分布对应的参数。
所以最大化似然函数的意义就是：通过使得样本集的联合概率最大来对参数进行估计，从而选择最佳的分布模型。
(4).EM算法
a.尝试用极大似然估计的方法来解GMM模型
解GMM模型，实际上就是确定GMM模型的参数(μ,Σ,π),使得由这组参数确定的GMM模型最有可能产生采样的样本。
先引入一个隐变量γ。它是一个K维二值随机变量，在它的K维取值中只有某个特定的元素γk的取值为1，其它元素的取值为0。实际上，隐变量描述的就是：每一次采样，选择第k个高斯模型的概率，故有:
p(γk=1)=πk。故样本y的概率为：
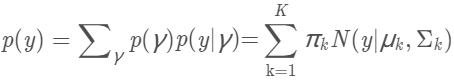
样本集Y(n个样本点)的联合概率为：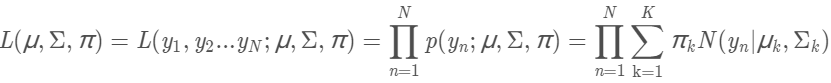
对数似然函数：
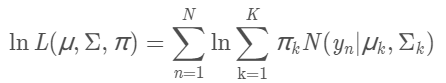
实际上没有办法通过求导的方法来求这个对数似然函数的最大值。如果我们已经清楚了某个变量服从的高斯分布，而且通过采样得到了这个变量的样本数据，想求高斯分布的参数，这时候极大似然估计可以胜任这个任务；而如果我们要求解的是一个混合模型，只知道混合模型中各个类的分布模型（譬如都是高斯分布）和对应的采样数据，而不知道这些采样数据分别来源于哪一类（隐变量），那这时候就可以借鉴EM算法。
b.EM算法估计GMM参数
引入一个变量 z,z=1表示是选择第1类的概率，z=2表示是选择第2类的概率。所以：
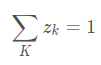
一般的用Y表示观测到的随机变量的数据，Z表示隐随机变量的数据(因为我们观测不到结果是从哪个概率分布中得出的，所以将这个叫做隐变量)。于是Y和Z连在一起被称为完全数据，仅Y一个被称为不完全数据。如果Z已知的话，那问题就可用极大似然估计求解了。
假设目标函数表示为：
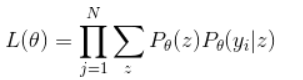
两边同时取对数ln:
为了表述的方便性，在这里用l(theta)代表lnL(theta).对于求解近似解，
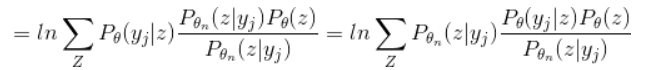
根据Jensen不等式有f(E[X])>=E[f(X)]，则:
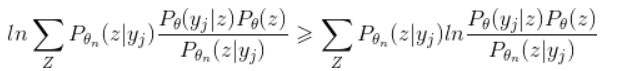
II项：
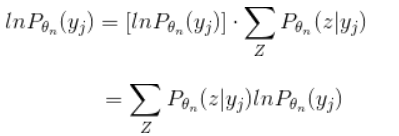
然后再把I-II合并起来看一下：
将右边的这一大串记为Q(\theta|\theta_n)，称为下边界函数，EM算法的目的是要取得目标函数的极大值，那么可以通过不断地提升下边界函数值来不断地提升目标函数的值，接下来，再看一下Q(\theta|\theta_n)，将其化简为便于优化迭代的形式：
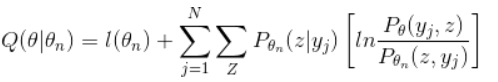
可以看到在等式的右边，由于我们之前的假设是\theta_n是已知的，那么把已知量和未知量分开：
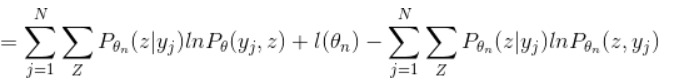
上式中，等号右边的第一项中带未知项，第二项和第三项都是常数，所以接下来的过程就简单了，我们只要对这个式子求偏导,求得此时取极大值时\theta的取值，这个值就是进入到下一步迭代是的概率分布参数值\theta_{n+1}，有了\theta_{n+1}之后就可以获得Q(\theta|\theta_{n+1})，然后不断地迭代直到收敛.
参考博客
https://blog.csdn.net/v_july_v/article/details/81708386
https://blog.csdn.net/u010834867/article/details/90762296?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1#%E4%B8%80%20%E6%A0%B7%E4%BE%8B%C2%A0%20%C2%A0%20%C2%A0%C2%A0
